비트코인 및 Layer2 자산 크로스체인 기술 분석

원제: 어댑터 서명 및 교차 체인 원자 교환에 대한 적용

원본 링크: https://blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/

원저자: mutourend, lynndel

1. 소개

비트코인의 레이어 2 확장 계획이 빠르게 발전함에 따라 비트코인과 레이어 2 대응 네트워크 간의 체인 간 자산 전송 빈도가 크게 증가했습니다. 이러한 추세는 Bitlayer와 같은 레이어 2 기술이 제공하는 더 높은 확장성, 더 낮은 거래 수수료 및 높은 처리량에 의해 주도됩니다. 이러한 발전은 보다 효율적이고 경제적인 거래를 촉진함으로써 다양한 애플리케이션 전반에 걸쳐 비트코인의 폭넓은 채택과 통합을 촉진합니다. 결과적으로 비트코인과 레이어 2 네트워크 간의 상호 운용성은 암호화폐 생태계의 핵심 구성 요소가 되어 혁신을 주도하고 사용자에게 더욱 다양하고 강력한 금융 도구를 제공하고 있습니다.

표 1에서 볼 수 있듯이 비트코인과 레이어 2 사이의 크로스체인 트랜잭션을 위한 세 가지 일반적인 솔루션, 즉 중앙 집중식 크로스체인 트랜잭션, BitVM 크로스체인 브리지 및 크로스체인 원자 스왑이 있습니다. 이 세 가지 기술은 신뢰 가정, 보안, 편의성, 거래 제한 등의 측면에서 서로 다르며 서로 다른 애플리케이션 요구 사항을 충족할 수 있습니다.

표 1. 크로스체인 거래 기술 비교

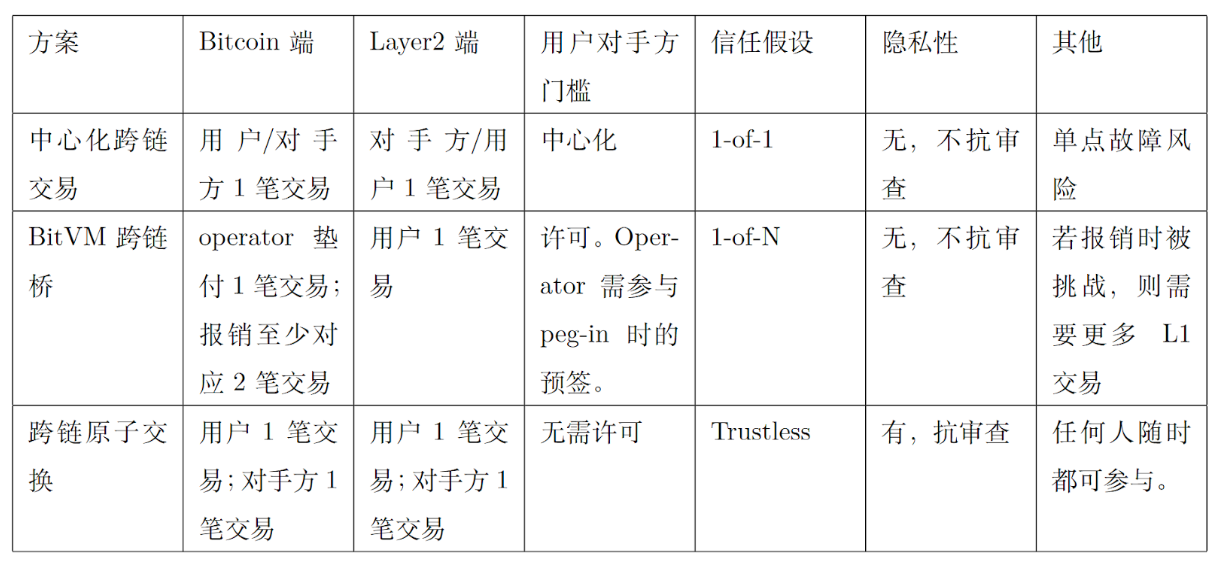
중앙화된 크로스체인 거래: 사용자는 먼저 중앙화된 기관(예: 프로젝트 당사자 또는 거래소)에 비트코인을 지불한 후, 중앙화된 기관은 Layer 2 네트워크에서 사용자가 지정한 주소로 동일한 가치의 자산을 지불합니다. 크로스체인 자산 거래 전송을 완료합니다. 이 기술의 장점은 중앙화된 기관에서 거래를 빠르게 확인하고 처리할 수 있기 때문에 속도가 빠르고 매칭 과정이 상대적으로 쉽다는 점이다. 그러나 이 방법의 보안은 전적으로 중앙화된 기관의 신뢰성에 달려 있습니다. 중앙 집중식 기관에 기술적 오류, 악의적인 공격 또는 불이행이 발생하면 사용자의 자금은 더 높은 위험에 직면하게 됩니다. 또한, 중앙화된 크로스체인 거래는 사용자의 개인 정보를 유출할 수도 있으므로 사용자는 이 방법을 선택할 때 신중하게 고려해야 합니다. 따라서 편의성과 효율성이 사용자에게 큰 편리함을 제공하지만 보안과 신뢰는 중앙화된 크로스체인 거래가 직면한 주요 과제입니다.

BitVM 크로스체인 브리지: 이 기술은 비교적 복잡합니다. 첫째, 페그인(Peg-in) 단계에서 사용자는 비트코인을 잠그기 위해 BitVM Alliance가 관리하는 다중 서명 주소에 비트코인을 지불합니다. 해당 수의 토큰이 레이어 2에서 발행되고 토큰은 레이어 2 트랜잭션 및 애플리케이션을 구현하는 데 사용됩니다. 사용자가 레이어 2 토큰을 파기하면 운영자는 지불금을 선지급합니다. 그 후, 운영자는 BitVM Alliance가 관리하는 다중 서명 풀에서 해당 수의 비트코인을 상환합니다. 운영자의 악행을 방지하기 위해 보상 프로세스는 낙관적 도전 메커니즘을 채택합니다. 즉, 모든 제3자가 악의적인 보상 행위에 도전하고 사악한 행위를 저지할 수 있습니다. 이 기술은 낙관적인 도전 메커니즘을 도입하므로 기술이 상대적으로 복잡합니다. 또한 낙관적 챌린지 메커니즘에는 더 높은 트랜잭션 수수료와 함께 많은 수의 챌린지 및 응답 트랜잭션이 포함됩니다. 따라서 BitVM 크로스체인 브리지는 U의 추가 발행과 마찬가지로 매우 큰 거래에만 적합하므로 사용 빈도가 낮습니다.

크로스체인 아토믹 스왑(Cross-chain Atomic Swap): 아토믹 스왑은 분산형 암호화폐 거래를 가능하게 하는 계약입니다. 이 맥락에서 "원자적"이란 한 자산의 소유권 변경이 실제로 다른 자산의 소유권 변경을 의미한다는 것을 의미합니다. 이 개념은 2013년 Bitcointalk 포럼에서 TierNolan이 처음 제안했습니다. 40년 동안 원자 교환은 이론의 영역에 머물렀습니다. Decred와 Litecoin이 원자 교환을 성공적으로 완료한 최초의 블록체인 시스템이 된 것은 2017년이 되어서였습니다. 아토믹 스왑에는 두 당사자가 참여해야 하며, 어떠한 제3자도 스왑 프로세스를 방해하거나 방해할 수 없습니다. 이는 해당 기술이 분산화되고 검열되지 않으며 개인 정보 보호가 우수하고 고주파 크로스체인 거래가 가능하여 분산형 거래소에서 널리 사용된다는 것을 의미합니다. 현재 크로스체인 아토믹 스왑에는 4개의 트랜잭션이 필요합니다. 일부 솔루션은 트랜잭션 수를 2개로 압축하려고 시도하지만 이로 인해 교환 당사자 모두의 실시간 온라인 요구 사항이 증가합니다. 마지막으로 크로스체인 원자 스왑 기술에는 주로 해시 시간 잠금 및 어댑터 서명이 포함됩니다.

해시 시간 잠금(HTLC) 기반 크로스 체인 원자 스왑: 크로스 체인 원자 스왑을 성공적으로 구현한 첫 번째 프로젝트는 "해시 잠금" 및 "시간 잠금"을 사용하여 온체인 스크립트의 도움으로 이를 달성하는 Decred입니다. (또는 스마트 계약) TierNolan이 제안한 원자 교환. HTLC를 사용하면 두 명의 사용자가 시간 제한이 있는 암호화폐 거래를 수행할 수 있습니다. 즉, 수신자는 지정된 시간(블록 번호 또는 블록 높이에 따라 결정됨) 내에 암호화 증명("비밀")을 계약서에 제출해야 합니다. 그렇지 않으면 자금이 반환됩니다. 보낸 사람. 수취인이 결제를 확인하면 거래가 성공합니다. 따라서 참여하는 두 블록체인 모두 "해시 잠금" 및 "시간 잠금" 기능을 보유해야 합니다.

HTLC 원자 교환은 분산 교환 기술 분야에서 획기적인 발전이지만 다음과 같은 문제가 있습니다. 이러한 아토믹 스왑 거래와 이와 관련된 데이터는 온체인에서 수행되므로 사용자 개인 정보 유출이 발생합니다. 즉, 교환이 있을 때마다 동일한 해시가 두 블록체인에 몇 개의 블록으로 구분되어 표시됩니다. 이는 관찰자가 교환에 참여하는 통화를 연관시킬 수 있음을 의미합니다. 즉, 서로 가까운 블록에서 동일한 해시 값을 찾을 수 있습니다(TimeStamp 방식). 체인 전반에 걸쳐 통화를 추적할 때 출처를 쉽게 확인할 수 있습니다. 이 분석에서는 관련 식별 데이터가 공개되지 않지만 제3자는 관련 행위자의 신원을 쉽게 추론할 수 있습니다.

어댑터 서명 기반 교차 체인 원자 교환: BasicSwap에서 제공하는 두 번째 유형의 스왑은 "어댑터 서명" 원자 교환이라고 하며, Monero 개발자 Joël Gugger가 2020년에 게시한 " 비트코인-모네로 교차 체인 원자 교환" 이라는 제목의 기사를 기반으로 합니다. }"종이. 이 문서는 Lloyd Fournier의 2019년 논문 One-Time Verifiously Encrypted Signatures, AKA Adapter Signatures 의 구현이라고 할 수 있습니다. 어댑터 서명은 초기 서명과 결합되어 비밀 데이터를 공개하는 추가 서명으로, 양 당사자가 두 데이터를 동시에 서로에게 공개할 수 있도록 하며, Monero의 원자 교환 쌍을 가능하게 하는 스크립트 없는 프로토콜의 핵심 구성 요소입니다.

HTLC 원자 스왑과 비교하여 어댑터 서명 기반 원자 스왑에는 3가지 장점이 있습니다. 첫째, 어댑터 서명 교환 체계는 시간 잠금 및 해시 잠금을 포함하여 "비밀 해시" 교환이 의존하는 온체인 스크립트를 대체합니다. 즉, HTLC 교환의 비밀과 비밀 해시는 어댑터 서명 교환에서 직접적인 대응이 없습니다. 따라서 비트코인 연구 커뮤니티에서는 이를 "스크립트 없는 스크립트"라고 부릅니다. 또한, 그러한 스크립트가 포함되지 않기 때문에 체인에서 차지하는 공간이 줄어들어 어댑터 서명을 기반으로 하는 원자 스왑이 더 가볍고 저렴해집니다. 마지막으로 HTLC는 각 체인이 동일한 해시 값을 사용해야 하며 어댑터 서명 원자 스왑과 관련된 트랜잭션을 연결할 수 없어 개인 정보 보호를 달성합니다.

이 기사에서는 먼저 Schnorr/ECDSA 어댑터 서명 및 크로스체인 원자 교환의 원리를 소개합니다. 그런 다음 어댑터 서명의 난수 보안 문제와 크로스 체인 시나리오의 시스템 이질성 및 알고리즘 이질성 문제를 분석하고 솔루션을 제공합니다. 마지막으로, 비대화형 디지털 자산 보관을 구현하기 위해 어댑터 서명이 확장 및 적용됩니다.

2. 어댑터 서명 및 크로스체인 원자 교환

2.1 Schnorr 어댑터 서명 및 원자 교환

2.2 ECDSA 어댑터 서명 및 원자 교환

2.2.1 영지식 증명 zk{v | Ṽ = v ᐧ G, V = v ᐧ Y}

3. 보안 문제 및 해결 방법

3.1 난수 문제와 해결책

3.1.1 난수 유출 문제

Schnorr/ECDSA 어댑터가 서명한 사전 서명은 모두 난수 $r$ å = r ᐧ G로 커밋됩니다. 또한, 영지식 증명은 $Ṽ=v ᐧ G, V=v ᐧ Y$를 난수 $v$에 커밋합니다. 난수가 유출되면 개인키도 유출됩니다.

구체적으로 Schnorr 프로토콜에서는 난수 $r$이 유출되면 다음 방정식에 따라 계산할 수 있습니다.

$ŝ = r + c x.$

개인 키 $x$를 계산합니다.

마찬가지로 ECDSA 프로토콜에서 난수 $r$가 누출되면 다음 방정식에 따라 계산할 수 있습니다.

$ŝ = r^{-1 }(해시(m)+R_x x).$

$x$를 얻기 위해 개인 키를 계산합니다.

마지막으로 영지식 증명 프로토콜에서 난수 $v$가 유출되면 다음 방정식에 따라 판별할 수 있습니다.

$z := v + c r.$

난수 $r$을 계산하고, 난수 $r$를 기반으로 개인 키 $x$를 추가로 계산합니다. 따라서 난수는 사용 후 즉시 삭제해야 합니다.

3.1.2 난수 재사용 문제

두 개의 크로스체인 트랜잭션에서 어댑터 서명 프로토콜이 동일한 난수를 사용하면 개인 키가 유출됩니다. 구체적으로 Schnorr 프로토콜에서 동일한 난수 $r$을 사용하면 다음 방정식 시스템에서는 $r$과 $x$만 알 수 없습니다.

$ŝ_ 1 =r + c_ 1 x, $

$ ŝ_ 2 = r + c_ 2 x.

따라서 방정식 시스템을 풀어 개인 키 $x$를 얻을 수 있습니다.

마찬가지로 ECDSA 어댑터 서명 프로토콜에서 동일한 난수 $r$가 사용되면 다음 방정식 시스템에서는 $r$ 및 $x$만 알 수 없습니다.

$ ŝ_ 1 = r^{-1 }(해시(m_ 1)+R_x x),$

$ ŝ_ 2 = r^{-1 }(해시(m_ 2)+R_x x).$

따라서 연립방정식을 풀어 개인 키 $x$를 얻을 수 있습니다.

마지막으로 영지식 증명 프로토콜에서 동일한 난수 $v$를 사용하면 다음 방정식 시스템에서는 $v$와 $r$만 알 수 없습니다.

$z_ 1 = v+c_ 1r, $

$ z_ 2 = v+c_ 2 $

따라서 연립방정식을 풀면 난수 $r$을 얻을 수 있고, 연립방정식을 더 풀면 개인 키 $x$를 얻을 수 있습니다.

비유하자면, 서로 다른 사용자가 동일한 난수를 사용하면 개인 키도 유출됩니다. 즉, 동일한 난수를 사용하는 두 사용자는 연립방정식을 풀고 서로의 개인키를 얻을 수 있습니다. 따라서 난수 재사용 문제를 해결하려면 RFC 6979를 사용해야 합니다.

3.1.3 해결 방법: RFC 6979

RFC 6979는 DSA 및 ECDSA를 사용하여 결정적 디지털 서명을 생성하는 방법을 지정하고 임의 값 k 생성과 관련된 보안 문제를 해결합니다. 기존 DSA 및 ECDSA 서명은 각 서명 작업에 대해 무작위로 생성되는 난수 k에 의존합니다. 이 난수가 재사용되거나 부적절하게 생성되면 개인 키의 보안이 손상될 수 있습니다. RFC 6979는 개인 키와 서명할 메시지에서 $k$를 결정론적으로 파생시켜 난수를 생성할 필요성을 제거합니다. 이렇게 하면 동일한 메시지가 동일한 개인 키로 서명될 때 서명이 항상 동일하므로 재현성과 예측 가능성이 향상됩니다. 특히 결정론적 $k$는 HMAC에 의해 생성됩니다. 이 프로세스에는 해시 함수(예: SHA 256)를 사용하여 개인 키, 메시지 및 카운터를 해싱하는 작업이 포함됩니다.

$k = SHA 256(sk, 메시지, 카운터).$

위 방정식에서는 표현의 단순화를 위해 개인 키 sk, 메시지 메시지 및 카운터 카운터에 대해서만 해시 값이 계산됩니다. 실제로 RFC 6979의 계산 프로세스에는 더 많은 해시 계산이 포함됩니다. 이 방정식은 k가 동일한 입력에 대해 재현 가능하면서 각 메시지에 대해 고유함을 보장하고 약하거나 손상된 난수 생성기와 관련된 개인 키 노출 위험을 줄입니다. 따라서 RFC 6979는 DSA 및 ECDSA를 사용하여 결정적 디지털 서명을 위한 강력한 프레임워크를 제공하고 난수 생성과 관련된 중요한 보안 문제를 해결하며 디지털 서명의 신뢰성과 예측 가능성을 향상시킵니다. 이는 높은 보안과 엄격한 운영 요구 사항 준수가 필요한 애플리케이션에 대한 귀중한 표준이 됩니다. Schnorr/ECDSA 서명에는 난수 결함이 있으므로 RFC 6979를 사용하여 방지해야 합니다. 따라서 Schnorr/ECDSA 기반 어댑터 서명에도 이러한 문제가 있으며 이러한 문제를 해결하려면 RFC 6979 사양을 사용해야 합니다.

3.2 크로스체인 시나리오 문제 및 해결 방법

3.2.1 UTXO와 계정 모델 시스템의 이질적인 문제와 해결책

그림 1에서 볼 수 있듯이 비트코인은 UTXO 모델을 사용하여 Secp 256 k 1 곡선을 기반으로 기본 ECDSA 서명을 구현합니다. Bitlayer는 Bitcoin L2 체인과 EVM 호환되며 Secp 256 k 1 곡선을 사용하고 기본 ECDSA 서명을 지원합니다. 어댑터 서명은 BTC 스왑에 필요한 논리를 구현하는 반면, Bitlayer 스왑 대응물은 Ethereum 스마트 계약의 힘으로 구동됩니다.

어댑터 서명을 기반으로 하는 체인 간 원자 스왑 또는 적어도 ECDSA 곡선과 작동하도록 설계된 반스크립트 없는 어댑터 서명 체계는 이더리움과 호환되지 않습니다. 그 이유는 이더리움은 UTXO 모델이 아닌 계정 모델이기 때문입니다. 특히, 어댑터 서명을 기반으로 하는 아토믹 스왑에서는 환불 거래가 사전 서명되어야 합니다. 하지만 이더리움 시스템에서는 nonce를 모르면 거래를 미리 서명할 수 없습니다. 따라서 당사자는 사전 서명 완료와 트랜잭션 실행 사이에 트랜잭션을 보낼 수 있습니다. 이로 인해 사전 서명된 트랜잭션이 무효화됩니다(nonce가 이미 사용되었으며 재사용할 수 없기 때문입니다).

또한 개인 정보 보호 관점에서 이는 Bitlayer 스왑의 익명성이 HTLC보다 우수하다는 것을 의미합니다(계약은 스왑 양쪽에서 찾을 수 있음). 그러나 한 당사자가 공개 계약을 맺어야 하기 때문에 Bitlayer 스왑은 어댑터 서명보다 익명성이 떨어집니다. 계약이 없는 측면에서 스왑 거래는 다른 거래처럼 보입니다. 그러나 EVM 계약 측면에서 거래는 분명히 자산 교환을 위한 것입니다. 한 당사자가 공개 계약을 갖고 있더라도 정교한 체인 분석 도구를 사용하더라도 이를 다른 체인으로 역추적하는 것은 불가능합니다.

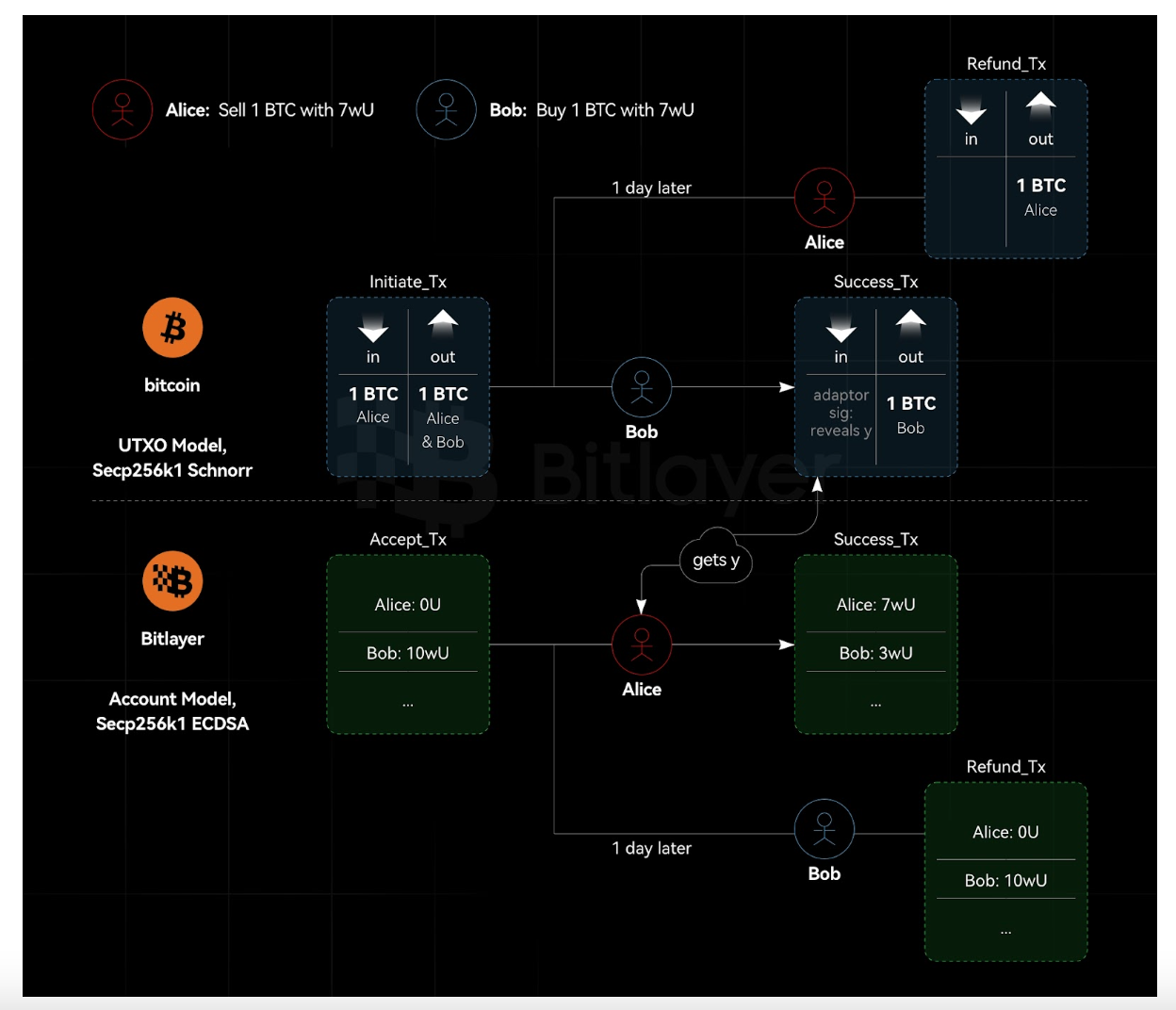
그림 1. UTXO 및 계정 모델 이종 시스템 크로스체인 원자 스왑

Bitlayer는 현재 기본 ECDSA 서명을 지원하며 스마트 계약을 통해 Schnorr 서명 확인을 구현할 수도 있습니다. 기본 Bitlayer 거래를 사용하는 경우 원자 교환으로 환불 거래에 사전 서명할 수 없습니다. 원자 교환을 달성하려면 Bitlayer 스마트 계약 거래를 사용해야 합니다. 그러나 이 프로세스는 개인 정보 보호를 희생합니다. 즉, Bitlayer 시스템에서 원자 교환에 참여하는 거래는 추적 가능하지만 BTC 시스템의 거래는 추적할 수 없습니다. Tornado Cash와 같은 Dapp 애플리케이션은 Bitlayer 측에서 BTC 및 Bitlayer 원자 스왑의 Bitlayer 측 거래에 대한 개인 정보 보호 서비스를 제공하도록 설계될 수 있습니다.

3.2.2 같은 곡선, 다른 알고리즘, 어댑터 서명 보안

그림 2에서 볼 수 있듯이 Bitcoin과 Bitlayer는 모두 Secp 256 k 1 곡선을 사용하지만 Bitcoin은 Schnorr 서명을 사용하고 Bitlayer는 ECDSA를 사용한다고 가정합니다. 이 경우 Schnorr 및 ECDSA를 기반으로 하는 어댑터 서명은 보안이 입증되었습니다. ECDSA 및 Schnorr 서명 오라클이 주어지면 시뮬레이터 S는 ECDSA를 깨기 위해 구성될 수 있고, 그런 다음 ECDSA 서명 오라클만 주어지면 시뮬레이터 S는 ECDSA를 깨뜨리도록 구성될 수 있습니다. 그러나 ECDSA는 안전합니다. 같은 방식으로, ECDSA 및 Schnorr 서명 오라클이 주어지면 시뮬레이터 S는 Schnorr 서명을 깨도록 구성될 수 있고, 그런 다음 ECDSA 서명 오라클만 주어지면 시뮬레이터 S는 Schnorr 서명을 깨도록 구성될 수 있습니다. 그러나 Schnorr 서명은 안전합니다. 따라서 크로스체인 시나리오에서 어댑터 서명은 동일한 곡선을 사용하지만 서명 알고리즘이 다르기 때문에 안전합니다. 즉, 어댑터 서명을 통해 한쪽 끝은 ECDSA를 사용하고 다른 쪽 끝은 Schnorr 서명을 사용할 수 있습니다.

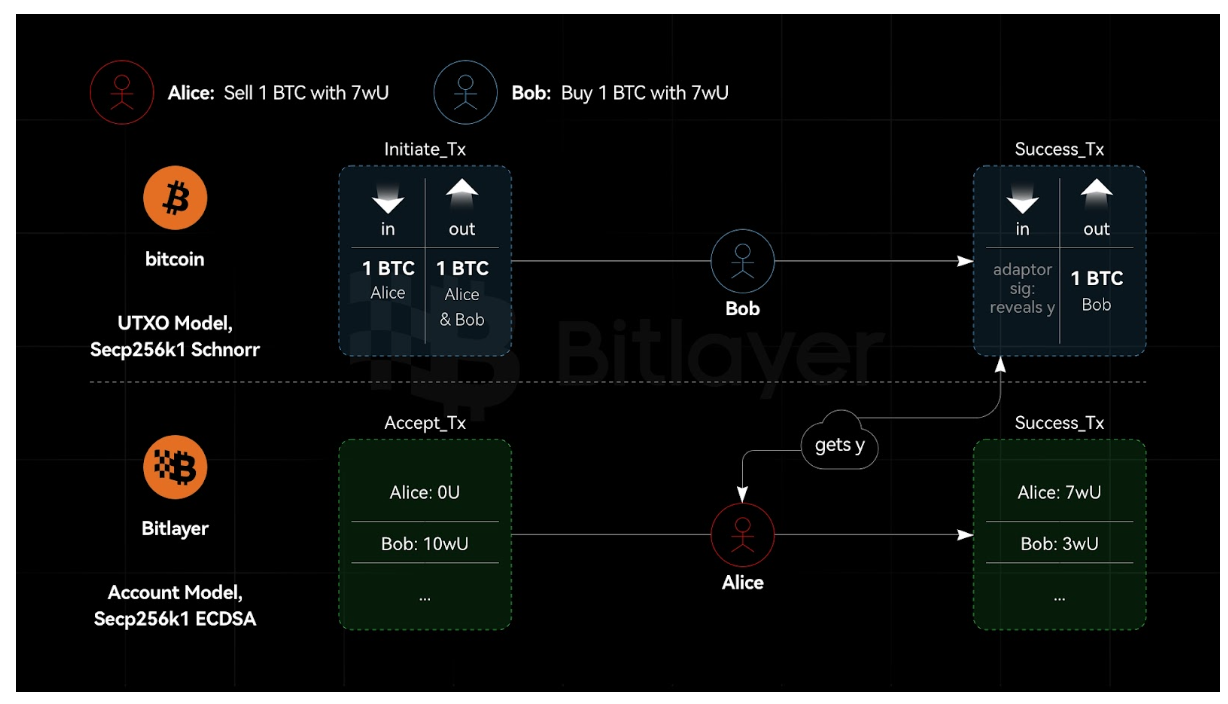
그림 2. 동일한 곡선, 다른 알고리즘, 어댑터 서명

3.2.3 다른 곡선, 어댑터 서명이 안전하지 않음

Bitcoin이 Secp 256 k 1 곡선과 ECDSA 서명을 사용하는 반면 Bitlayer는 ed 25519 곡선과 Schnorr 서명을 사용한다고 가정합니다. 이 경우 어댑터 서명을 사용할 수 없습니다. 곡선이 다르기 때문에 타원 곡선 그룹의 순서가 다릅니다. 즉, 모듈 계수가 다릅니다. Bob이 비트코인 시스템의 ECDSA 서명에 $y$를 적용하면 $s:= ŝ+y$가 계산됩니다. 이때 $y$의 값 공간은 Secp 256 k 1 타원 곡선 그룹의 스칼라 공간입니다. 그런 다음 Alice는 $y$를 사용하여 ed 25519 타원 곡선 그룹에 대해 Schnorr 서명을 수행해야 합니다. 그러나 ed 25519 곡선의 cofactor는 8이고, 모듈 계수는 Secp 256 k 1 타원 곡선 그룹의 모듈 계수와 동일하지 않습니다. 따라서 ed 25519 곡선의 Schnorr 서명에 $y$를 사용하는 것은 안전하지 않습니다.

4. 디지털 자산 보관 신청

디지털 자산 보관에는 구매자 Alice, 판매자 Bob 및 관리인이라는 세 명의 참가자가 있습니다. 어댑터 서명을 사용하면 비대화형 임계값 디지털 자산 보관이 가능해지고 상호작용 없이 임계값 지출 전략의 하위 집합이 인스턴스화됩니다. 이 하위 집합은 초기화에 참여하는 참가자와 초기화에 참여하지 않는 참가자, 후자를 관리인이라고 부르는 두 가지 유형의 참가자로 구성됩니다. 관리인은 임의의 거래에 서명할 수 없으며 지원 당사자 중 한 명에게만 비밀을 보냅니다.

한편, 관리인은 몇 가지 고정 결제 거래 중에서만 선택할 수 있으며 다른 당사자 중 하나와 새로운 거래에 서명할 수 없습니다. 따라서 이 비밀 해제 메커니즘은 비대화형 임계값 호스팅을 임계값 Schnorr 서명보다 덜 유연하게 만듭니다. 반면, 임계값 Schnorr 서명을 사용하여 2/3 지출 정책을 설정할 수 있습니다. 그러나 임계값 Schnorr 서명 프로토콜에서는 분산형 키 생성 프로토콜을 실행하기 위해 세 당사자가 필요합니다. 따라서 어댑터 서명을 기반으로 하는 자산 에스크로 프로토콜은 비대화형이라는 장점이 있습니다.

4.1 어댑터 서명을 기반으로 한 비대화형 자산 보관

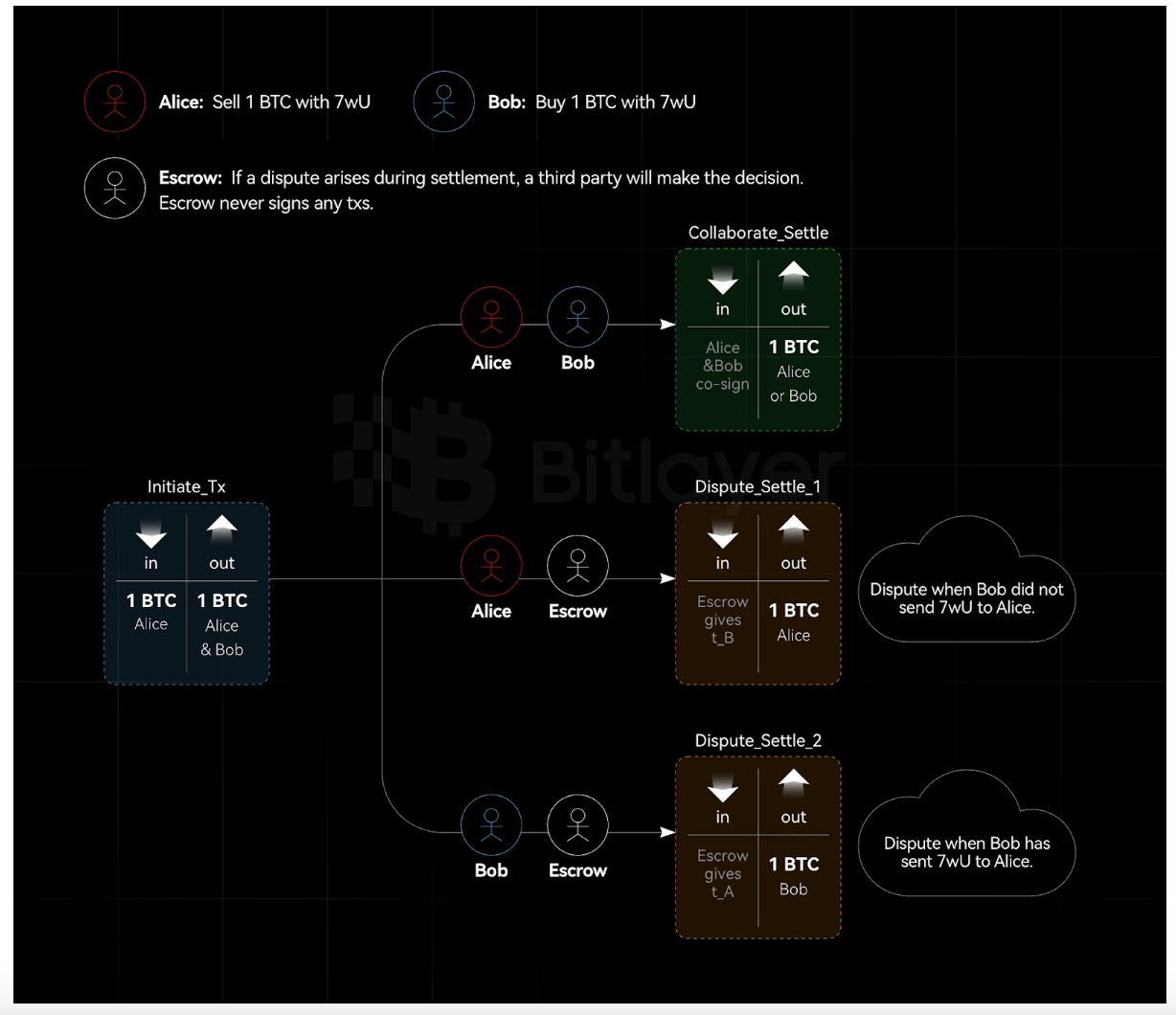
그림 3. 어댑터 서명을 기반으로 한 비대화형 자산 호스팅

그림 3에서 볼 수 있듯이 Alice와 Bob은 관리인을 포함하는 숨겨진 전략을 사용하여 2-of-3 트랜잭션 출력을 생성하려고 합니다. $c$ 조건에 따라 Alice 또는 Bob은 트랜잭션 출력을 사용할 수 있습니다. Alice와 Bob 사이에 분쟁이 있는 경우 관리인(공개 키 $E$, 개인 키 $e$)은 Alice 또는 Bob이 자산을 얻을지 여부를 결정합니다.

• Alice와 Bob 사이의 2/2 MuSig 출력으로 BTC를 보내는 서명되지 않은 자금 거래를 생성합니다.

• Alice는 임의의 값 $t_A$를 선택하고 어댑터가 $t_A ᐧ G$인 트랜잭션의 Schnorr 사전 서명 $(\hat{R}_A,\hat{s}_A)$를 Bob에게 보냅니다. 출력은 Bob에게 전송됩니다. Alice는 또한 비밀 $t_A$의 \textbf{검증 가능한 암호화}$가 포함된 암호문을 Bob에게 보내고 에스크로 공개 키 $E$를 $E_c = E + hash(E, c)G$ C = Enc로 조정합니다. (E_c, t_A)$. 이 과정에서 Bob은 Alice의 사전 서명을 받은 후 자신의 서명을 추가합니다. 이는 2-of-2 MuSig를 충족하지 못하므로 자금 출력을 사용할 수 없습니다. Bob이 $t_A$(에스크로에서 제공)를 알고 있거나 Alice가 추가로 전체 서명에 서명하여 Bob에게 보내는 경우에만 자금 출력을 사용할 수 있습니다.

• 이에 따라 Bob은 자신의 어댑터 암호 $t_B$를 기반으로 단계 (2)를 반복합니다. 이때 Bob이 서명한 트랜잭션은 자금 출력을 Alice에게 보내는 것입니다.

• Alice와 Bob은 모두 수신한 암호문의 유효성을 확인하고 해당 암호문이 $E_c$의 비밀을 암호화한 것임을 확인함으로써 자금 거래에 서명하고 브로드캐스팅합니다. 검증 가능한 암호화를 사용하면 관리인이 설정 단계에 참여할 필요가 없으며 공개 계약 $c$도 필요하지 않습니다.

• 분쟁이 발생하면 Alice와 Bob은 암호문과 조건 c를 관리인에게 보낼 수 있고, 관리인은 실제 상황을 판단하고 조정된 개인 키 $e+hash(E, c)$를 사용하여 복호화하고 $t_A를 보낼 수 있습니다. /t_B $ 밥/앨리스에게.

분쟁이 없으면 Alice와 Bob은 2/2 MuSig 출력을 원하는 대로 사용할 수 있습니다. 분쟁이 있는 경우 어느 쪽이든 에스크로에 연락하여 어댑터 비밀번호 $t_A$ 또는 $t_B$를 요청할 수 있습니다. 따라서 당사자 중 하나는 에스크로 당사자의 도움을 받아 어댑터 서명을 완료하고 결제 거래를 방송할 수 있습니다.

4.2 검증 가능한 암호화

이산 로그를 기반으로 하는 기존의 검증 가능한 암호화 체계( 이산 로그의 실제 검증 가능한 암호화 및 복호화 )는 특별히 구조화된 그룹의 검증만 지원하기 때문에 Secp 256 k 1 어댑터와 함께 사용할 수 없습니다.

현재 Secp 256k 1 이산 로그를 기반으로 검증 가능한 암호화를 수행하는 두 가지 유망한 방법, 즉 Purify 와 Juggling이 있습니다.

Purify는 원래 결정론적 논스(DN)를 사용하여 MuSig 프로토콜을 생성하도록 제안되었으며, 각 서명자는 자신의 논스가 공개 키와 메시지에 의사 난수 함수(PRF)를 올바르게 적용한 결과임을 증명하기 위해 영지식을 사용해야 합니다. Purify PRF는 Secp 256 k 1 이상의 이산 로그에 대한 검증 가능한 암호화 체계를 생성하기 위해 Bulletproofs 영지식 프로토콜의 산술 회로에서 효율적으로 구현됩니다. 즉, 검증 가능한 암호화를 위해 zkSnark를 사용하세요.

저글링 암호화에는 네 단계가 포함됩니다. (1) 이산 로그 $x$를 $x = \sum _k 2 ^{(k-1)l} x_k$가 되도록 길이 $l$의 여러 세그먼트 $x_k$로 분할합니다. 2) 공개 키 $Y$ $\{ D_k, E_k\} = \{ x_k ᐧ G + r_k ᐧ Y, r_k ᐧ G \}$를 사용하여 조각 $x_k ᐧ G$의 ElGamal 암호화 (3) 범위 증명 생성; 각 $x_k ᐧ G$에 대해 $D_k$가 Pedersen 약속 $x_k ᐧ G + r_k ᐧ Y$이고 그 값이 $ 2 ^l$보다 작음을 증명합니다. (4) 시그마 프로토콜을 사용하여 $ \{sum D_k, sum E_k\}$는 $x_k ᐧ G$의 올바른 암호화입니다.

복호화 과정에서는 각 $x_k ᐧ G$를 $\{D_k, E_k\}$에 대해 복호화한 후 $x_k$을 철저하게 검색합니다(값 범위는 $[ 0, 2 ^l)$입니다).

Purify는 Bulletproofs 내에서 PRF를 실행해야 하는데, 이는 상대적으로 복잡한 반면 저글링은 이론적으로 더 간단합니다. 또한, 증명 크기, 증명 시간 및 검증 시간의 차이는 매우 작습니다.

5. 요약

이 문서에서는 Schnorr/ECDSA 어댑터 서명 및 체인 간 원자 교환의 원리에 대한 자세한 설명을 제공합니다. 어댑터 서명의 난수 유출 및 중복 문제에 대한 심층 분석이 수행되었으며, 이러한 문제를 해결하기 위해 RFC 6979의 사용이 제안되었습니다. 또한, 크로스체인 적용 시나리오에서는 UTXO 모델과 블록체인의 계정 모델 간의 차이뿐만 아니라 어댑터 서명이 다른 알고리즘, 다른 곡선 및 기타 기능을 지원하는지 여부도 고려해야 한다는 점을 자세히 분석합니다. 문제. 마지막으로, 비대화형 디지털 자산 보관을 실현하기 위해 어댑터 서명이 확장 및 적용되고, 관련된 암호화 기본 요소(검증 가능한 암호화)가 간략하게 소개됩니다.

참고자료

• Gugger J. 비트코인-모네로 크로스체인 원자 스왑[J], 암호화 ePrint 아카이브, 2020.

• Fournier L. 확인 가능하게 암호화된 일회성 서명, 일명 어댑터 서명[J].

• https://crypto-in-action.github.io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf

• Pornin T. 디지털 서명 알고리즘(DSA) 및 타원 곡선 디지털 서명 알고리즘(ECDSA)[R]의 결정론적 사용.

• Komlo C, Goldberg I. FROST: 유연한 라운드 최적화 Schnorr 임계값 서명[C]//암호화의 선택 영역: 제27차 국제 컨퍼런스, Halifax, NS, 캐나다(가상 이벤트), 2020년 10월 21-23일, 개정된 선택 논문 27 . 스프링거 국제 출판, 2021: 34-65.

• https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/NITE.md

• https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swap/

• Camenisch J, Shoup V. 이산 로그의 실제 검증 가능한 암호화 및 암호 해독[C]//Annual International Cryptology Conference. 베를린, 하이델베르그: Springer Berlin Heidelberg, 2003: 126-144.

• Nick J, Ruffing T, Seurin Y, 외 MuSig-DN: 검증 가능한 결정론적 nonce를 사용한 Schnorr 다중 서명[C]//컴퓨터 및 통신 보안에 관한 2020 ACM SIGSAC 회의 절차: 1717-1731.

• Shlomovits O, Leiba O. Jugglingswap: 스크립트 없는 원자 교차 체인 교환[J] arXiv 사전 인쇄 arXiv: 2007.14423, 2020.