ビットコインとレイヤー2資産クロスチェーンテクノロジーの分析

原題: アダプター署名とクロスチェーン アトミック スワップへのその応用

元のリンク: https://blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/

原作者: ミュートゥエンド、リンデル

1 はじめに

ビットコインのレイヤー 2 拡張計画の急速な発展に伴い、ビットコインとそのレイヤー 2 対応ネットワーク間のクロスチェーン資産転送の頻度が大幅に増加しました。この傾向は、ビットレイヤーなどのレイヤー 2 テクノロジーによって提供される、より高いスケーラビリティ、より低いトランザクション手数料、および高いスループットによって推進されています。これらの進歩により、より効率的かつ経済的なトランザクションが促進され、それによってさまざまなアプリケーションにわたるビットコインの幅広い採用と統合が促進されます。その結果、ビットコインとレイヤー2ネットワーク間の相互運用性が暗号通貨エコシステムの重要な要素となり、イノベーションを推進し、より多様で強力な金融ツールをユーザーに提供しています。

表 1 に示すように、ビットコインとレイヤー 2 間のクロスチェーン トランザクションには、集中型クロスチェーン トランザクション、BitVM クロスチェーン ブリッジ、クロスチェーン アトミック スワップの 3 つの典型的なソリューションがあります。これら 3 つのテクノロジーは、信頼の前提、セキュリティ、利便性、トランザクション制限などの点で異なり、さまざまなアプリケーションのニーズを満たすことができます。

表 1. クロスチェーントランザクションテクノロジーの比較

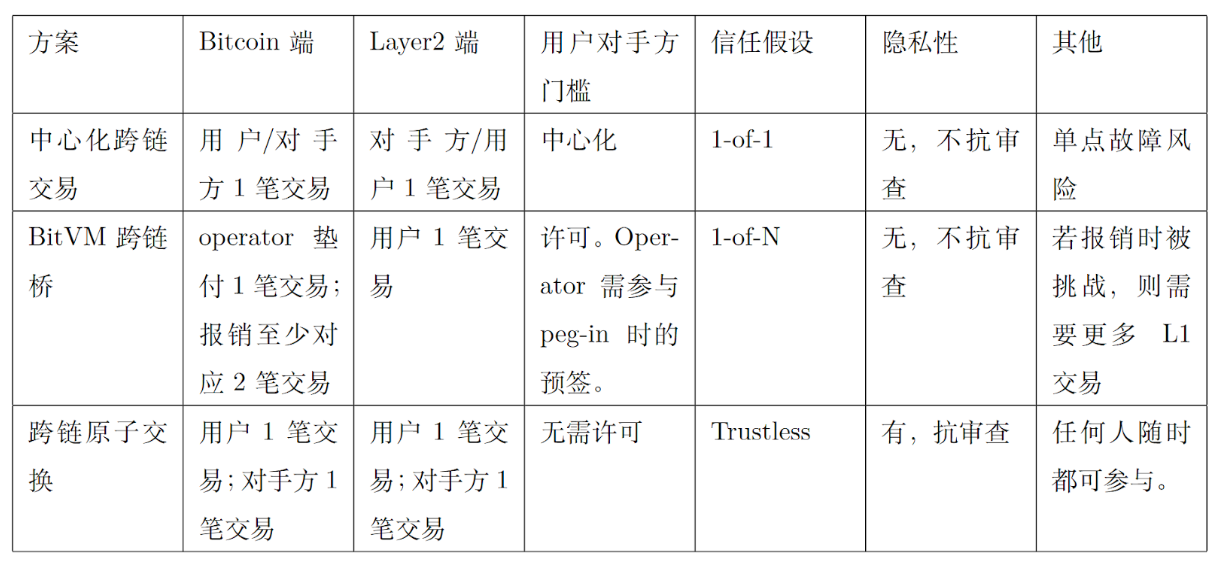
集中型クロスチェーントランザクション:ユーザーはまず集中型機関 (プロジェクト関係者や取引所など) にビットコインを支払い、次に集中型機関がレイヤー 2 ネットワーク上のユーザーが指定したアドレスに同価値の資産を支払います。クロスチェーン資産トランザクションの転送を完了します。このテクノロジーの利点は、中央機関が取引を迅速に確認して処理できるため、高速であり、照合プロセスが比較的簡単であることです。ただし、この方法の安全性は、中央機関の信頼性と信頼性に完全に依存しています。中央機関が技術的な障害、悪意のある攻撃、または債務不履行に遭遇した場合、ユーザーの資金はより高いリスクに直面することになります。さらに、一元化されたクロスチェーントランザクションはユーザーのプライバシーを漏らす可能性があるため、ユーザーはこの方法を選択する際に慎重に検討する必要があります。したがって、その利便性と効率性はユーザーに大きな利便性をもたらしますが、集中化されたクロスチェーントランザクションが直面する主な課題はセキュリティと信頼です。

BitVM クロスチェーン ブリッジ:このテクノロジーは比較的複雑です。まず、ペグイン段階で、ユーザーは BitVM Alliance が管理するマルチシグネチャ アドレスにビットコインを支払い、ビットコインをロックします。対応する数のトークンがレイヤー 2 で生成され、そのトークンはレイヤー 2 のトランザクションとアプリケーションの実装に使用されます。ユーザーがレイヤー 2 トークンを破棄すると、オペレーターが支払いを前払いします。その後、オペレータは、BitVM Alliance が管理するマルチシグネチャ プール内の対応する数のビットコインを払い戻します。オペレーターによる悪事を防ぐために、払い戻しプロセスには楽観的なチャレンジメカニズムが採用されています。つまり、第三者は悪意のある払い戻し行為に異議を申し立て、邪悪な行為を阻止することができます。このテクノロジは楽観的チャレンジ メカニズムを導入しているため、テクノロジは比較的複雑です。さらに、オプティミスティック チャレンジ メカニズムには、多数のチャレンジ トランザクションとレスポンス トランザクションが含まれ、トランザクション手数料が高くなります。したがって、BitVM クロスチェーン ブリッジは、U の追加発行と同様、非常に大規模なトランザクションにのみ適しているため、使用頻度は低くなります。

クロスチェーン アトミック スワップ:アトミック スワップは、分散型暗号通貨取引を可能にする契約です。この文脈において、「アトミック」とは、ある資産の所有権の変更が実際には別の資産の所有権の変更を意味することを意味します。この概念は、2013 年に TierNolan によって Bitcointalk フォーラムで初めて提案されました。 40年間、アトミック・スワップは理論の領域に留まっていた。 Decred と Litecoin がアトミック スワップを成功裏に完了した最初のブロックチェーン システムになったのは 2017 年のことでした。アトミック スワップには 2 者が関与する必要があり、第三者はスワップ プロセスを中断したり妨害したりすることはできません。これは、このテクノロジーが分散型で無検閲であり、プライバシー保護が優れており、高頻度のクロスチェーントランザクションを実現できるため、分散型取引所で広く使用されていることを意味します。現在、クロスチェーン アトミック スワップには 4 つのトランザクションが必要です。一部のソリューションではトランザクション数を 2 つに圧縮しようとしていますが、これにより、交換の双方にとってリアルタイムのオンライン要件が増加します。最後に、クロスチェーン アトミック スワップ テクノロジには、主にハッシュ タイム ロックとアダプタ署名が含まれます。

ハッシュ タイム ロック (HTLC) に基づくクロスチェーン アトミック スワップ:クロスチェーン アトミック スワップの実装に成功した最初のプロジェクトは Decred です。このプロジェクトでは、オンチェーン スクリプトの助けを借りて「ハッシュ ロック」と「タイム ロック」を使用してそれを実現します。 TierNolan によって提案されたアトミック スワップ (またはスマート コントラクト)。 HTLC を使用すると、2 人のユーザーが時間制限のある暗号通貨取引を行うことができます。つまり、受信者は指定された時間 (ブロック番号またはブロックの高さによって決定される) 内に暗号証明 (「秘密」) を契約に提出する必要があり、そうでない場合、資金はユーザーに返還されます。送信者によって。受取人が支払いを確認すると、取引は成功です。したがって、参加する両方のブロックチェーンには「ハッシュロック」と「タイムロック」機能が必要です。

HTLC アトミック交換は分散型交換技術の分野における大きな進歩ですが、次のような問題があります。これらのアトミック スワップ トランザクションとそれに関連するデータはオンチェーンで実行され、ユーザーのプライバシー漏洩につながります。言い換えれば、交換が行われるたびに、同じハッシュが両方のブロックチェーンに表示されますが、そのハッシュはわずか数ブロックしか離れていません。これは、オブザーバーが交換に参加している通貨を相関付けることができること、つまり、（タイムスタンプ的に）互いに近いブロックで同じハッシュ値を見つけることができることを意味します。チェーン全体で通貨を追跡する場合、ソースを特定するのは簡単です。この分析では関連する識別データは明らかになりませんが、第三者は関係者の身元を簡単に推測できます。

アダプター署名ベースのクロスチェーン アトミック スワップ: BasicSwap が提供する 2 番目のタイプのスワップは、「アダプター署名」アトミック スワップと呼ばれます。これは、Monero 開発者 Joël Gugger が 2020 年に公開した「ビットコインとモネロのクロスチェーン アトミック スワップ」というタイトルの記事に基づいています。 }"紙。この論文は、Lloyd Fournier の 2019 年の論文「One-Time Verifiively Encrypted Signatures (別名アダプター署名)」の実装であると言えます。アダプター署名は、秘密データを明らかにするために初期署名と組み合わせられる追加の署名であり、双方が両方のデータを同時にお互いに公開できるようになり、Monero のアトミック スワップ ペアを可能にするスクリプトレス プロトコルの重要なコンポーネントです。

HTLC アトミックスワップと比較して、アダプター署名ベースのアトミック スワップには 3 つの利点があります。 まず、アダプター署名交換スキームは、タイム ロックやハッシュ ロックなど、「秘密ハッシュ」交換が依存するオンチェーン スクリプトを置き換えます。つまり、HTLC 交換のシークレットとシークレット ハッシュは、アダプター署名交換では直接対応しません。したがって、ビットコイン研究コミュニティでは、これを「スクリプトレス スクリプト」と呼んでいます。さらに、そのようなスクリプトが関与しないため、チェーン上で占有されるスペースが削減され、アダプターの署名に基づくアトミック スワップがより軽量かつ安価になります。最後に、HTLC では各チェーンが同じハッシュ値を使用する必要があり、アダプター署名アトミックスワップに含まれるトランザクションはリンクできないため、プライバシー保護が実現されます。

この記事では、まず Schnorr/ECDSA アダプターの署名とクロスチェーンのアトミック交換の原理を紹介します。次に、アダプターの署名に存在する乱数のセキュリティ問題と、クロスチェーン シナリオにおけるシステムの異質性とアルゴリズムの異質性の問題を分析し、解決策を提供します。最後に、アダプターの署名が拡張され、非対話型のデジタル資産保管を実現するために適用されます。

2. アダプターの署名とクロスチェーンのアトミックスワップ

2.1 Schnorr アダプターの署名とアトミック交換

2.2 ECDSA アダプターの署名とアトミック交換

2.2.1 ゼロ知識証明 zk{v Ṽ = v ᐧ G, V = v ᐧ Y}

3. セキュリティの問題と解決策

3.1 乱数の問題と解決策

3.1.1 乱数漏洩問題

Schnorr/ECDSA アダプターによって署名された事前署名はすべて、乱数 $r$ Œ = r ᐧ G にコミットされます。さらに、ゼロ知識証明は乱数 $v$ を $Ṽ=v ᐧ G, V=v ᐧ Y$ にコミットします。乱数が漏洩すると秘密鍵も漏洩してしまいます。

具体的には、Schnorr プロトコルでは、乱数 $r$ が漏洩した場合、次の式に従って計算できます。

$ŝ = r + c x.$

秘密鍵 $x$ を計算します。

同様に、ECDSA プロトコルでは、乱数 $r$ が漏洩した場合、次の式に従って計算できます。

$ŝ = r^{-1 }(ハッシュ(m)+R_x x).$

秘密鍵を計算して $x$ を取得します。

最後に、ゼロ知識証明プロトコルでは、乱数 $v$ が漏洩した場合、次の式に従って決定できます。

$z := v + c r.$

乱数$r$を計算し、さらに乱数$r$に基づいて秘密鍵$x$を計算する。したがって、乱数は使用後すぐに削除する必要があります。

3.1.2 乱数再利用問題

2 つのクロスチェーン トランザクションで、アダプター署名プロトコルが同じ乱数を使用すると、秘密キーが漏洩します。具体的には、Schnorr プロトコルでは、同じ乱数 $r$ が使用される場合、次の連立方程式では $r$ と $x$ だけが不明になります。

$ŝ_ 1 =r + c_ 1 x, $

$ ŝ_ 2 = r + c_ 2 x。

したがって、連立方程式を解くと秘密鍵 $x$ を取得できます。

同様に、ECDSA アダプター署名プロトコルでは、同じ乱数 $r$ が使用される場合、次の連立方程式では $r$ と $x$ のみが不明になります。

$ ŝ_ 1 = r^{-1 }(ハッシュ(m_ 1)+R_x x),$

$ ŝ_ 2 = r^{-1 }(ハッシュ(m_ 2)+R_x x).$

したがって、連立方程式を解くと秘密鍵 $x$ を取得できます。

最後に、ゼロ知識証明プロトコルでは、同じ乱数 $v$ が使用される場合、次の連立方程式では $v$ と $r$ だけが不明になります。

$z_ 1 = v+c_ 1 r、$

$ z_ 2 = v+c_ 2 r.

したがって、連立方程式を解くと乱数 $r$ が得られ、さらに連立方程式を解くと秘密鍵 $x$ が得られます。

同様に、異なるユーザーが同じ乱数を使用した場合、秘密鍵も漏洩します。つまり、2 人のユーザーが同じ乱数を使用して連立方程式を解き、お互いの秘密鍵を取得できます。したがって、乱数の再利用に対処するには RFC 6979 を使用する必要があります。

3.1.3 解決策: RFC 6979

RFC 6979 は、DSA と ECDSA を使用して決定論的なデジタル署名を生成する方法を指定し、乱数値 k の生成に関連するセキュリティ問題に対処します。従来の DSA および ECDSA 署名は、署名操作ごとにランダムに生成される乱数 k に依存します。この乱数が再利用されたり、不適切に生成されたりすると、秘密キーのセキュリティが危険にさらされる可能性があります。 RFC 6979 では、秘密鍵と署名されるメッセージから $k$ を決定的に導出することにより、乱数を生成する必要がなくなりました。これにより、同じメッセージが同じ秘密鍵で署名される場合、署名は常に同じになるため、再現性と予測可能性が高まります。具体的には、決定論的な $k$ が HMAC によって生成されます。このプロセスには、ハッシュ関数 (SHA 256 など) を使用して秘密キー、メッセージ、カウンターをハッシュすることが含まれます。

$k = SHA 256(sk, msg, counter).$

上の式では、表現を簡単にするために、秘密キー sk、メッセージ msg、およびカウンター counter のハッシュ値のみが計算されています。実際には、RFC 6979 の計算プロセスにはさらに多くのハッシュ計算が含まれます。この方程式により、k がメッセージごとに一意であると同時に、同じ入力に対して再現可能であることが保証され、弱い乱数生成器または侵害された乱数生成器に関連する秘密鍵漏洩のリスクが軽減されます。したがって、RFC 6979 は、DSA と ECDSA を使用した決定論的デジタル署名のための強力なフレームワークを提供し、乱数生成に関連する重大なセキュリティ問題に対処し、デジタル署名の信頼性と予測可能性を強化します。このため、高いセキュリティと厳格な運用要件への準拠を必要とするアプリケーションにとって価値のある標準となっています。 Schnorr/ECDSA 署名には乱数の欠陥があるため、RFC 6979 を使用して防止する必要があります。したがって、Schnorr/ECDSA ベースのアダプター署名にもこれらの問題があり、これらの問題を解決するには RFC 6979 仕様を使用する必要があります。

3.2 クロスチェーンシナリオの問題と解決策

3.2.1 UTXO およびアカウント モデル システムの異種問題と解決策

図 1 に示すように、ビットコインは UTXO モデルを使用して、Secp 256 k 1 曲線に基づくネイティブ ECDSA 署名を実装します。 Bitlayer は、ビットコイン L2 チェーンと互換性のある EVM であり、Secp 256 k 1 曲線を使用し、ネイティブ ECDSA 署名をサポートします。アダプターの署名は BTC スワップに必要なロジックを実装しますが、ビットレイヤーのスワップ対応物はイーサリアム スマート コントラクトの力を利用しています。

アダプター署名、または少なくとも ECDSA 曲線で動作するように設計された半スクリプトレスのアダプター署名スキームに基づくクロスチェーン アトミック スワップは、イーサリアムと互換性がありません。その理由は、イーサリアムは UTXO モデルではなくアカウント モデルであるためです。具体的には、アダプターの署名に基づくアトミック スワップでは、返金トランザクションに事前署名する必要があります。ただし、イーサリアム システムでは、ノンスを知らなければトランザクションに事前署名することはできません。したがって、当事者は、事前署名の完了とトランザクションの実行の間にトランザクションを送信する可能性があります。これにより、事前署名されたトランザクションが無効になります (nonce はすでに使用されており、再利用できないため)。

さらに、プライバシーの観点から見ると、これは、ビットレイヤー スワップの匿名性が HTLC よりも優れていることを意味します (コントラクトはスワップの両側で確認できます)。ただし、一方の当事者が公的契約を結ぶ必要があるため、ビットレイヤー スワップはアダプター署名よりも匿名性が低くなります。契約がなければ、スワップ取引は他の取引と同じように見えます。しかし、EVM契約側としては、この取引は明らかに資産交換のためのものである。一方の当事者が公的契約を結んでいても、高度なチェーン分析ツールを使用したとしても、それを別のチェーンまで遡ることは不可能です。

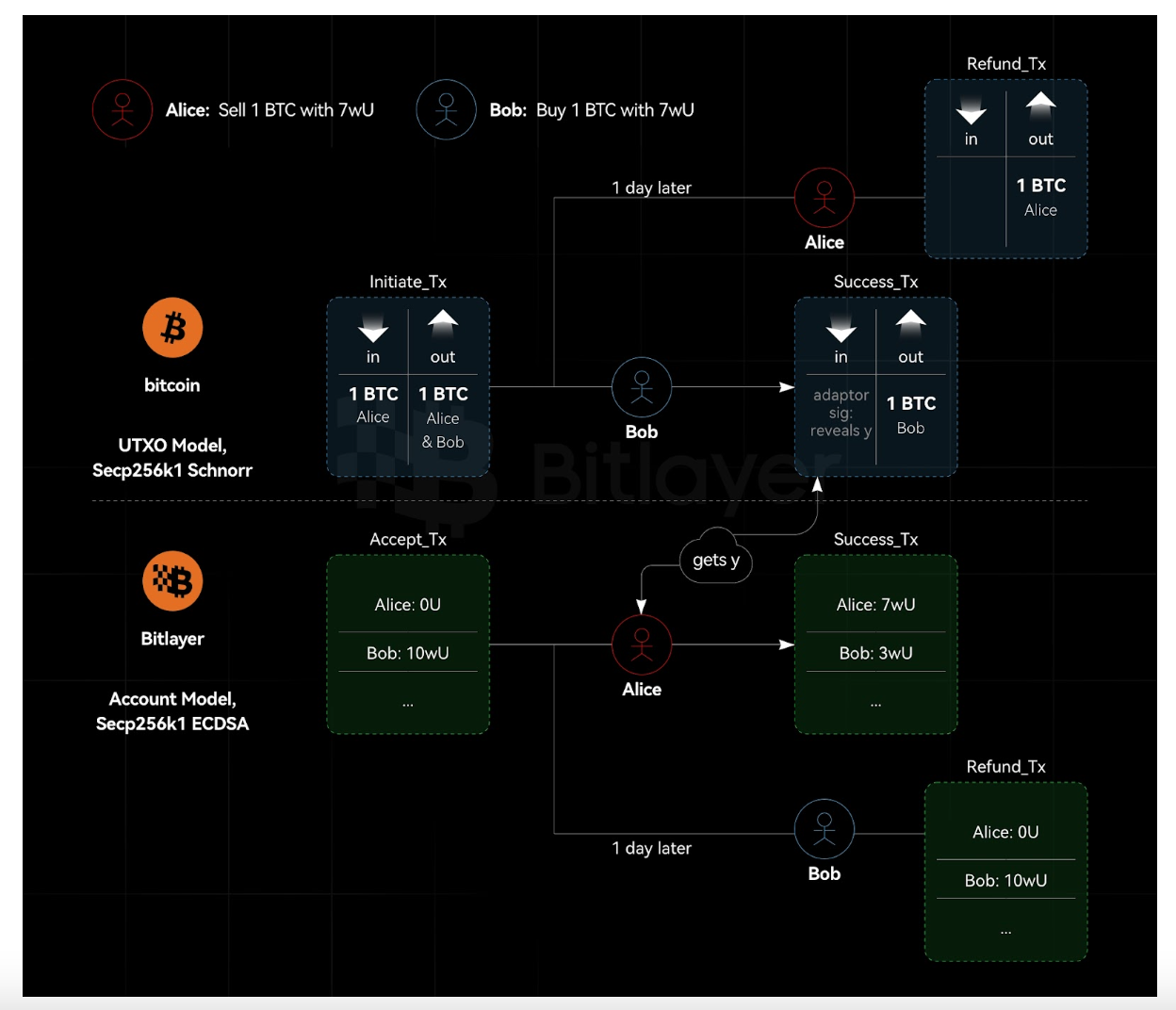
図 1. UTXO とアカウント モデルの異種システムのクロスチェーン アトミック スワップ

Bitlayer は現在、ネイティブ ECDSA 署名をサポートしており、スマート コントラクトを通じて Schnorr 署名検証を実装することもできます。ネイティブ Bitlayer トランザクションを使用する場合、アトミック スワップで返金トランザクションに事前署名することはできません。アトミック スワップを実現するには、Bitlayer スマート コントラクト トランザクションを使用する必要があります。ただし、このプロセスではプライバシーが犠牲になります。つまり、ビットレイヤー システムのアトミック スワップに参加しているトランザクションは追跡可能ですが、BTC システムのトランザクションは追跡できません。 Tornado Cash のような Dapp アプリケーションは、BTC およびビットレイヤー アトミック スワップにおけるビットレイヤー側のトランザクションにプライバシー サービスを提供するためにビットレイヤー側で設計できます。

3.2.2 同じ曲線、異なるアルゴリズム、アダプター署名のセキュリティ

図 2 に示すように、ビットコインとビットレイヤーの両方が Secp 256 k 1 曲線を使用しているが、ビットコインは Schnorr 署名を使用し、ビットレイヤーは ECDSA を使用していると仮定します。この場合、Schnorr と ECDSA に基づくアダプター署名は安全であることが証明されています。 ECDSA および Schnorr 署名オラクルが与えられた場合、シミュレータ S は ECDSA を破るように構築できると仮定すると、ECDSA 署名オラクルが与えられた場合にのみ、シミュレータ S は ECDSA を破るために構築できます。ただし、ECDSA は安全です。同様に、ECDSA および Schnorr 署名オラクルが与えられた場合、シミュレータ S が Schnorr 署名を解読するように構築できると仮定すると、ECDSA 署名オラクルのみが与えられた場合、シミュレータ S は Schnorr 署名を解読するように構築できます。ただし、Schnorr 署名は安全です。したがって、クロスチェーンのシナリオでは、アダプターの署名は同じ曲線を使用しますが、異なる署名アルゴリズムを使用するため、安全です。つまり、アダプター署名により、一方の端で ECDSA を使用し、もう一方の端で Schnorr 署名を使用できるようになります。

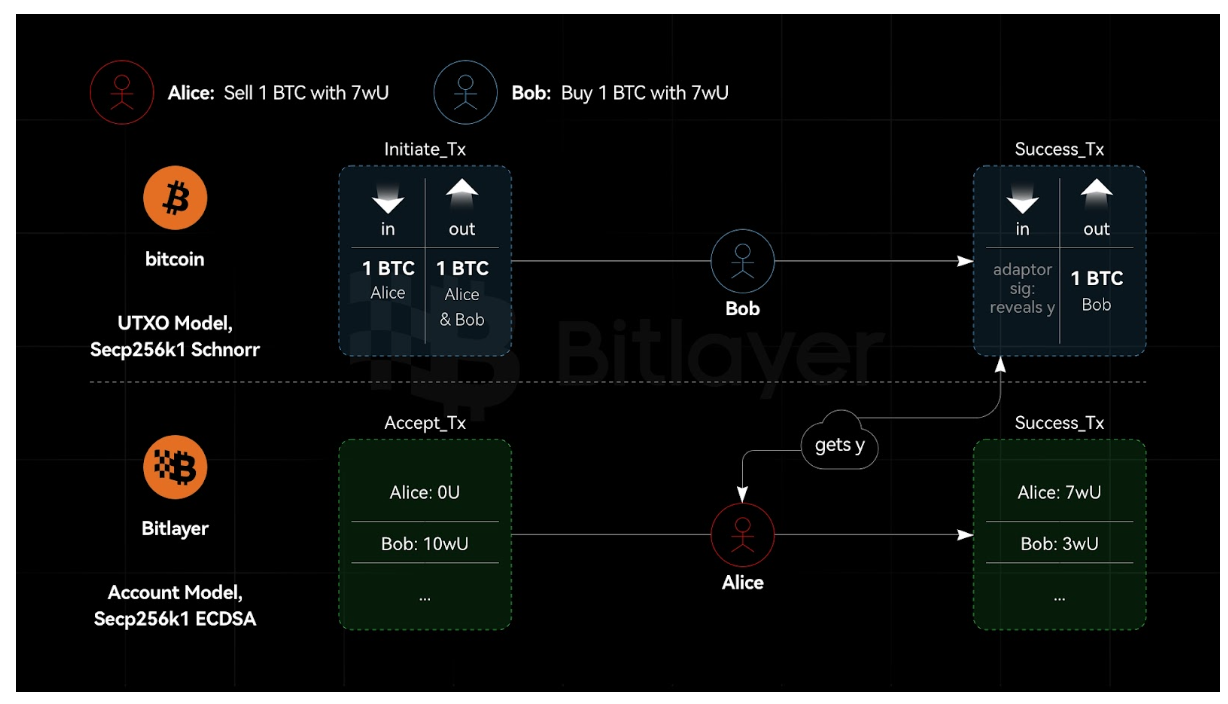
図 2. 同じ曲線、異なるアルゴリズム、アダプタ シグネチャ

3.2.3 異なる曲線、アダプターの署名は安全ではありません

ビットコインは Secp 256 k 1 曲線と ECDSA 署名を使用し、Bitlayer は ed 25519 曲線と Schnorr 署名を使用すると仮定します。この場合、アダプター署名は使用できません。曲線が異なるため、楕円曲線グループの次数が異なります。つまり、モジュール係数が異なります。ボブが $y$ をビットコイン システムの ECDSA 署名に適合させると、$s:= ŝ+y$ が計算されます。このとき、$y$の値空間はSecp 256 k 1 楕円曲線群のスカラー空間となる。次に、アリスは $y$ を使用して ed 25519 楕円曲線グループに対してシュノア署名を実行する必要があります。ただし、ed 25519 曲線の余因子は 8 であり、モジュール係数は Secp 256 k 1 楕円曲線グループのモジュール係数と等しくありません。したがって、ed 25519 曲線上の Schnorr 署名に $y$ を使用するのは安全ではありません。

4.デジタル資産保管アプリケーション

デジタル資産の保管には、購入者のアリス、販売者のボブ、保管者の 3 人の参加者がいます。アダプター署名を使用すると、非対話型のしきい値デジタル資産保管が可能になり、対話なしでしきい値支出戦略のサブセットがインスタンス化されます。このサブセットは、初期化に参加する参加者と初期化に参加しない参加者という 2 種類の参加者で構成され、後者はカストディアンと呼ばれます。管理者は任意のトランザクションに署名することはできず、サポートする当事者の 1 つにのみシークレットを送信します。

一方で、カストディアンはいくつかの固定決済取引から選択することしかできず、他の当事者のいずれかと新しい取引に署名することはできません。したがって、この秘密解放メカニズムにより、非対話型のしきい値ホスティングはしきい値 Schnorr 署名よりも柔軟性が低くなります。一方、2/3 の支出ポリシーは、しきい値 Schnorr 署名を使用して設定できます。ただし、しきい値 Schnorr 署名プロトコルでは、3 者が分散鍵生成プロトコルを実行する必要があります。したがって、アダプター署名に基づく資産エスクロー プロトコルには、非対話型であるという利点があります。

4.1 アダプター署名に基づく非対話型資産保管

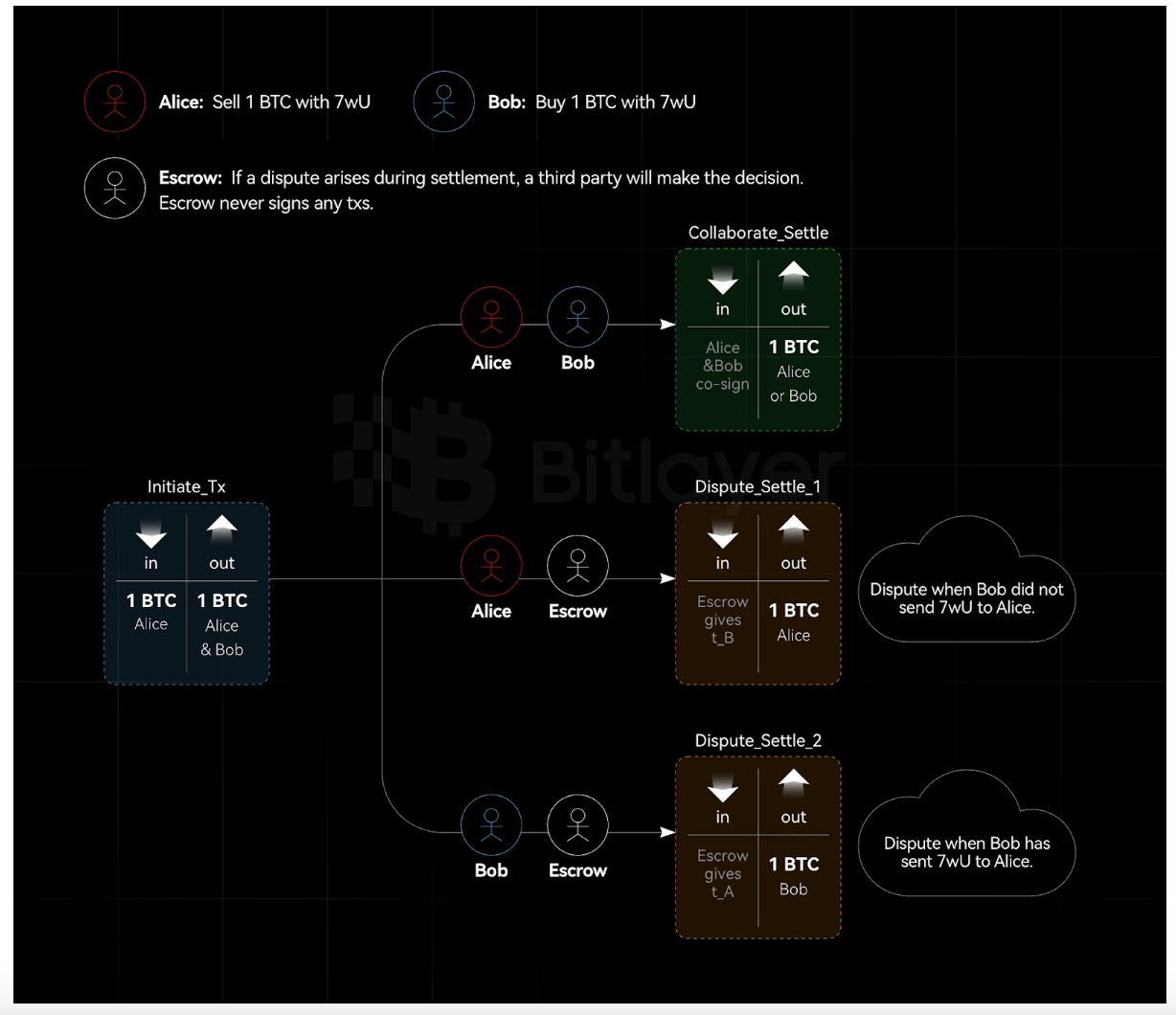
図 3. アダプター署名に基づく非対話型アセット ホスティング

図 3 に示すように、アリスとボブは、カストディアンを含むステルス戦略を使用して 2/3 トランザクション出力を作成したいと考えています。条件 $c$ に応じて、アリスまたはボブがトランザクション出力を使用できます。アリスとボブの間で紛争が生じた場合、管理者 (公開鍵 $E$、秘密鍵 $e$) が、アリスとボブのどちらが資産を取得するかを決定します。

• アリスとボブ間の 2-of2 MuSig 出力に BTC を送信する署名なしの資金トランザクションを作成します。

• アリスはランダムな値 $t_A$ を選択し、アダプターが $t_A ᐧ G$ であるトランザクションの Schnorr 事前署名 $(\hat{R}_A,\hat{s}_A)$ をボブに送信します。出力はボブに送信されます。また、アリスは、秘密 $t_A$ の \textbf{検証可能な暗号化}$ を含む暗号文をボブに送信し、エスクロー公開鍵 $E$ を $E_c = E + hash(E, c)G$ C = Enc に調整します。 (E_c, t_A)$。このプロセス中、ボブはアリスの事前署名を受け取った後、自分の署名を追加しますが、これは 2-of-2 MuSig を満たさないため、資金出力を使用できません。資金出力は、ボブが $t_A$ (エスクローによって提供される) を知っている場合、またはアリスが追加で完全な署名に署名してボブに送信した場合にのみ使用できます。

• 同様に、ボブはアダプターの秘密 $t_B$ に基づいてステップ (2) を繰り返します。現時点では、ボブによって署名されたトランザクションは、資金出力をアリスに送信することになっています。

• アリスとボブは両方とも、受信した暗号文の有効性を検証し、その暗号文が $E_c$ の秘密の暗号化であることを確認し、それによって資金調達トランザクションに署名してブロードキャストします。検証可能な暗号化により、管理者がセットアップ段階に参加する必要がなく、公的契約 $c$ も必要ありません。

• 紛争が生じた場合、アリスとボブは暗号文と条件 c を管理者に送信でき、管理者は実際の状況を判断し、調整された秘密鍵 $e+hash(E, c)$ を使用して復号化して $t_A を送信できます。 /t_B $ をボブ/アリスに送信します。

議論がなければ、アリスとボブは 2-of2 MuSig 出力を好きなように使うことができます。紛争が生じた場合、いずれかの当事者がエスクローに連絡し、アダプターの秘密 $t_A$ または $t_B$ を要求することができます。したがって、一方の当事者は、エスクロー当事者の助けを借りて、アダプターの署名を完了し、決済トランザクションをブロードキャストできます。

4.2 検証可能な暗号化

離散対数に基づく従来の検証可能な暗号化スキーム (離散対数の実用的な検証可能な暗号化と復号化) は、特別に構造化されたグループの検証のみをサポートするため、Secp 256 k 1 アダプタでは使用できません。

現在、Secp 256 k 1 離散対数に基づいて検証可能な暗号化を実行するには、 PurifyとJugglingという 2 つの有望な方法があります。

Purify は当初、決定論的ノンス (DN) を使用して MuSig プロトコルを作成することが提案されており、各署名者はゼロ知識を使用して、そのノンスが公開キーとメッセージに擬似乱数関数 (PRF) を正しく適用した結果であることを証明する必要があります。 Purify PRF は、Bulletproofs ゼロ知識プロトコルの算術回路に効率的に実装されており、Secp 256 k 1 上の離散対数で検証可能な暗号化スキームを作成します。つまり、検証可能な暗号化には zkSnark を使用します。

ジャグリング暗号化には 4 つのステップが含まれます。 (1) $x = \sum _k 2 ^{(k-1)l} x_k$ のように、離散対数 $x$ を長さ $l$ の複数のセグメント $x_k$ に分割します。 2) 公開鍵 $Y$ を使用したフラグメント $x_k ᐧ G$ の ElGamal 暗号化 $\{ D_k, E_k\} = \{ x_k ᐧ G + r_k ᐧ Y, r_k ᐧ G \}$ (3 ) 範囲証明を作成します。各 $x_k ᐧ G$ について、$D_k$ が Pedersen コミットメント $x_k ᐧ G + r_k ᐧ Y$ であり、その値が $ 2 ^l$ より小さいことを証明します。 (4) シグマ プロトコルを使用して $ を証明します。 \{sum D_k, sum E_k\}$ は $x_k ᐧ G$ の正しい暗号化です。

復号処理では、各 $x_k ᐧ G$ を $\{D_k, E_k\}$ に対して復号し、$x_k$ を網羅的に検索します (値の範囲は $[ 0, 2 ^l)$ です)。

Purify では、Bulletproofs 内で PRF を実行する必要がありますが、これは比較的複雑ですが、Juggling は理論的には簡単です。さらに、証明サイズ、証明時間、検証時間における 2 つの違いは非常に小さいです。

5. まとめ

この記事では、Schnorr/ECDSA アダプターの署名とクロスチェーンのアトミック交換の原理について詳しく説明します。アダプター署名における乱数の漏洩と重複の問題の詳細な分析が行われ、これらの問題を解決するために RFC 6979 の使用が提案されました。さらに、クロスチェーンアプリケーションシナリオでは、UTXOモデルとブロックチェーンのアカウントモデルの違いだけでなく、アダプターの署名が異なるアルゴリズム、異なる曲線などをサポートしているかどうかも考慮する必要があることが詳細に分析されます。問題。最後に、非対話型デジタル資産管理を実現するためにアダプター署名が拡張および適用され、関連する暗号化プリミティブ (検証可能な暗号化) が簡単に紹介されます。

参考文献

• Gugger J. ビットコインとモネロのクロスチェーン アトミック スワップ [J]、暗号学の ePrint アーカイブ、2020 年。

• Fournier L. ワンタイム検証可能に暗号化された署名、別名アダプター署名 [J] 2019、2019。

• https://crypto-in-action.github.io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf

• ポーニン T. デジタル署名アルゴリズム (DSA) と楕円曲線デジタル署名アルゴリズム (ECDSA) の決定的使用法 [R] 2013。

• Komlo C、Goldberg I. FROST: 柔軟なラウンド最適化シュノアしきい値署名[C]//暗号化の選択領域: 第 27 回国際会議、ニューサウスウェールズ州ハリファックス、カナダ (仮想イベント)、2020 年 10 月 21 ～ 23 日、改訂された厳選論文 27シュプリンガー・インターナショナル・パブリッシング、2021: 34-65。

• https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/NITE.md

• https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps/

• Camenisch J、Shoup V. 離散対数の実用的な検証可能な暗号化と復号化[C]//年次国際暗号学会、ベルリン、ハイデルベルク: Springer Berlin Heidelberg、2003: 126-144。

• Nick J、Ruffing T、Seurin Y、他、MuSig-DN: 検証可能な決定論的ナンスを含む Schnorr マルチ署名 [C]//2020 年 ACM SIGSAC Conference on Computer and Communications Security の議事録: 1717-1731。

• Shlomovits O、Leiba O. Jugglingswap: スクリプトレス アトミック クロスチェーン スワップ [J]。arXiv プレプリント arXiv: 2007.14423、2020。