소개: Gonka PoW 2.0의 핵심 메커니즘

Gonka PoW 2.0의 핵심 아이디어는 기존의 작업 증명(PoW)을 의미 있는 AI 컴퓨팅 작업으로 전환하는 것입니다. 본 글에서는 두 가지 핵심 메커니즘, 즉 계산 과제 생성과 부정행위 방지 검증을 자세히 살펴보겠습니다. 또한, 이 혁신적인 합의 메커니즘이 어떻게 연산 유용성을 보장하는 동시에 신뢰할 수 있는 부정행위 방지 보호 장치를 구축하는지 보여줄 것입니다.

전체 과정은 다음 다이어그램으로 요약할 수 있습니다.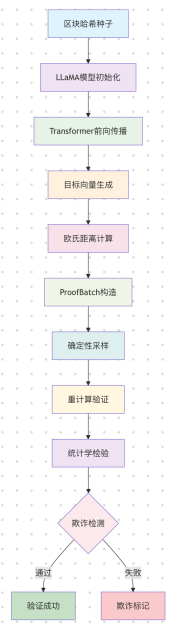

1. 계산 과제 생성 메커니즘

Gonka PoW 2.0의 핵심은 연산 과제로, 기존의 작업 증명 방식을 의미 있는 AI 컴퓨팅 작업으로 전환합니다. 기존 PoW와 달리 Gonka의 연산 과제는 단순한 해시 계산이 아니라, 네트워크 보안을 보장할 뿐만 아니라 사용 가능한 연산 결과를 생성하는 완전한 딥러닝 추론 프로세스입니다.

1.1 종자 시스템의 통합 관리

모든 계산은 통합된 시드(seed)에 의해 구동되어 네트워크의 모든 노드가 동일한 계산 작업을 실행하도록 보장합니다. 이러한 설계는 모든 노드가 유효한 결과를 얻기 위해 동일한 계산 작업을 실행해야 하므로 계산의 재현성과 공정성을 보장합니다.

데이터 출처 : mlnode/packages/pow/src/pow/compute/compute.py#L217-L225

종자 시스템의 핵심 요소는 다음과 같습니다.

- 블록 해시 : 컴퓨팅 작업의 일관성을 보장하는 마스터 시드 역할을 합니다.

-공개 키 : 컴퓨팅 노드의 신원을 식별합니다.

- 블록 높이 : 시간 동기화를 보장합니다.

-매개변수 구성 : 제어 모델 아키텍처 및 계산 복잡도

1.2 LLaMA 모델 가중치의 결정적 초기화

각 계산 작업은 블록 해싱을 통해 결정론적으로 초기화되는 가중치를 갖는 통합된 LLaMA 모델 아키텍처로 시작합니다. 이러한 설계는 모든 노드가 동일한 모델 구조와 초기 가중치를 사용하도록 하여 일관된 계산 결과를 보장합니다.

데이터 출처 : mlnode/packages/pow/src/pow/models/llama31.py#L32-L51

가중치 초기화의 수학적 원리:

- 정규 분포 : N(0, 0.02²) - 분산이 작아 기울기 안정성이 보장됨

- 결정론 : 동일한 블록 해시는 동일한 가중치를 생성합니다.

- 메모리 효율성 : 비디오 메모리 사용량을 줄이기 위해 float16 정밀도를 지원합니다.

1.3 타겟 벡터 생성 및 거리 계산

목표 벡터는 고차원 단위 구에 균일하게 분포하는데, 이는 계산 과제의 공정성을 결정하는 핵심 요소입니다. 고차원 공간에 균일하게 분포된 목표 벡터를 생성함으로써 계산 과제의 무작위성과 공정성이 보장됩니다.

데이터 출처 : mlnode/packages/pow/src/pow/random.py#L165-L177

4096차원 어휘 공간에서 구면 기하학은 다음과 같은 속성을 갖습니다.

-단위 길이 :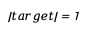

-각도 분포 : 두 개의 임의 벡터 사이의 각도는 90°가 되는 경향이 있습니다.

- 집중 현상 : 대부분의 질량이 구의 표면 근처에 분포함

구면 위의 균일 분포에 대한 수학적 원리:

n차원 공간에서 단위 구면의 균일 분포는 다음과 같이 생성될 수 있습니다.

1. 먼저 n개의 독립적인 표준 정규 분포 확률 변수를 생성합니다.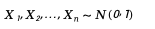

2. 그런 다음 정규화합니다.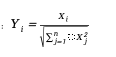

이 방법을 사용하면 생성된 벡터가 구면에 균등하게 분포되며, 수학적 표현은 다음과 같습니다.

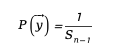
~에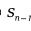 n-1 구의 표면적은 다음과 같습니다.

거리 계산은 계산 결과를 검증하는 데 중요한 단계입니다. 계산의 효율성은 모델 출력과 목표 벡터 사이의 유클리드 거리를 계산하여 측정합니다.

데이터 출처 : mlnode/packages/pow/src/pow/compute/compute.py의 처리 로직 기반

거리 계산 단계:

1. 순열 응용 프로그램 : 순열 시드에 따라 출력 차원을 재배열합니다.

2. 벡터 정규화 : 모든 출력 벡터가 단위 구에 있는지 확인합니다.

3. 거리 계산 : 타겟 벡터까지의 유클리드 거리를 계산합니다.

4. 배치 캡슐화 : 결과를 ProofBatch 데이터 구조로 캡슐화합니다.

2. 부정행위 방지 검증 메커니즘

연산 과제의 공정성과 보안을 보장하기 위해, 시스템은 정교한 부정행위 방지 검증 시스템을 설계했습니다. 이 메커니즘은 결정론적 샘플링과 통계적 검증을 통해 연산의 진위를 검증하여 악의적인 노드가 부정행위를 통해 부당한 이익을 얻는 것을 방지합니다.

2.1 ProofBatch 데이터 구조

계산 결과는 검증 프로세스의 핵심 요소인 ProofBatch 데이터 구조에 캡슐화됩니다. ProofBatch는 컴퓨팅 노드의 신원 정보, 타임스탬프, 그리고 계산 결과를 포함하여 후속 검증에 필요한 데이터 기반을 제공합니다.

데이터 출처 : mlnode/packages/pow/src/pow/data.py#L8-L25

ProofBatch 데이터 구조의 특성:

- ID : 공개 키는 컴퓨팅 노드를 고유하게 식별합니다.

- 블록체인 바인딩 : block_hash와 block_height가 시간 동기화를 보장합니다.

- 계산 결과 : nonce와 dist는 모든 시도와 거리 값을 기록합니다.

- 하위 배치 지원 : 임계값을 충족하는 성공적인 계산 추출 지원

2.2 결정론적 샘플링 메커니즘

검증 효율성을 높이기 위해 시스템은 결정론적 샘플링 메커니즘을 사용하여 계산 결과 전체가 아닌 일부 결과만 검증합니다. 이러한 설계는 검증의 효율성을 보장할 뿐만 아니라 검증 비용을 크게 절감합니다.

Gonka의 검증 샘플링 속도는 전체 네트워크에서 일관성을 보장하기 위해 체인상 매개변수를 통해 균일하게 관리됩니다.

데이터 출처 : inference-chain/proto/inference/inference/params.proto#L75-L78

데이터 출처 : inference-chain/x/inference/types/params.go#L129-L133

시드 시스템을 기반으로 샘플링 프로세스는 완전히 결정론적이어서 검증의 공정성을 보장합니다. SHA-256 해시 함수와 검증자의 공개 키, 블록 해시, 블록 높이 및 기타 정보를 사용하여 시드를 생성함으로써 모든 검증자는 동일한 샘플링 전략을 사용하게 됩니다.

데이터 출처 : decentralized-api/mlnodeclient/poc.go#L175-L201

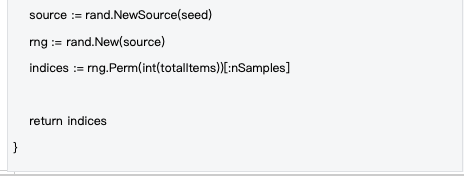
결정론적 샘플링의 장점:

- 공정성 : 모든 검증자는 동일한 샘플링 전략을 사용합니다.

- 효율성 : 검증 비용을 줄이기 위해 데이터의 일부만 검증합니다.

- 보안성 : 샘플링된 데이터를 예측하기 어려워 부정행위를 방지할 수 없음

2.3 통계적 사기 탐지

이 시스템은 이항 분포 검정을 사용하여 사기를 탐지하고, 통계적 방법을 사용하여 컴퓨팅 노드의 정직성을 판단합니다. 이 방법은 하드웨어 정밀도와 계산 복잡도를 기반으로 예상 오류율을 설정하고, 통계적 검정을 사용하여 이상 징후를 탐지합니다.

데이터 출처 : mlnode/packages/pow/src/pow/data.py#L7

예상 오류율은 다음 요소를 고려하여 설정됩니다.

-부동 소수점 정밀도 : 하드웨어 간 부동 소수점 정밀도 차이

- 병렬 컴퓨팅 : GPU 병렬화로 인한 수치 누적 오류

- 무작위성 : 모델 가중치 초기화에 작은 차이가 있음

- 시스템 차이점 : 다양한 운영 체제와 드라이버 간의 컴퓨팅 동작 차이점

데이터 출처 : mlnode/packages/pow/src/pow/data.py#L174-L204

요약: 안전하고 안정적인 AI 컴퓨팅 네트워크 구축

Gonka PoW 2.0은 신중하게 설계된 연산 과제와 부정행위 방지 검증 메커니즘을 통해 블록체인의 보안 요구 사항과 AI 컴퓨팅의 실질적인 가치를 성공적으로 결합했습니다. 연산 과제는 작업의 의미를 보장하는 동시에 부정행위 방지 메커니즘은 네트워크의 공정성과 보안을 보장합니다.

이 설계는 "의미 있는 채굴"의 기술적 실행 가능성을 검증할 뿐만 아니라 분산형 AI 컴퓨팅에 대한 새로운 기준을 수립합니다. 컴퓨팅은 안전하고 유용해야 하며, 검증 가능하고 효율적이어야 합니다.

Gonka PoW 2.0은 통계, 암호화, 분산 시스템 설계를 결합하여 계산적 유용성을 보장하는 동시에 신뢰할 수 있는 부정행위 방지 메커니즘을 성공적으로 구축하여 "의미 있는 채굴"의 기술적 경로에 대한 견고한 보안 기반을 제공했습니다.

참고: 이 문서는 Gonka 프로젝트의 실제 코드 구현 및 설계 문서를 기반으로 합니다. 모든 기술 분석 및 구성 매개변수는 해당 프로젝트의 공식 코드 저장소에서 가져왔습니다.

Gonka.ai 소개

Gonka는 효율적인 AI 컴퓨팅 파워를 제공하도록 설계된 탈중앙화 네트워크입니다. Gonka의 설계 목표는 글로벌 GPU 컴퓨팅 파워를 최대한 활용하여 의미 있는 AI 워크로드를 완료하는 것입니다. 중앙화된 게이트키퍼를 제거함으로써 Gonka는 개발자와 연구자에게 컴퓨팅 리소스에 대한 허가 없는 접근을 제공하는 동시에 모든 참여자에게 GNK 토큰을 보상으로 제공합니다.

Gonka는 미국 AI 개발사 Product Science Inc.에서 인큐베이팅되었습니다. 웹 2 업계 베테랑이자 Snap Inc.의 전 핵심 제품 책임자였던 Libermans 형제가 설립한 이 회사는 2023년 OpenAI 투자자 Coatue Management, Solana 투자자 Slow Ventures, K5, Insight, Benchmark Partners 등의 투자자들로부터 1,800만 달러를 성공적으로 유치했습니다. 이 프로젝트의 초기 참여자로는 6 Blocks, Hard Yaka, Gcore, Bitfury 등 웹 2-웹 3 분야의 유명 기업들이 있습니다.

공식 웹사이트 | Github | X | Discord | 백서 | 경제 모델 | 사용자 매뉴얼