DAOrayaki: 가짜 zkSNARK 증명 만들기

DAOrayaki

特邀专栏作者

2021-12-28 12:05

이 기사는 약 2559자로, 전체를 읽는 데 약 4분이 소요됩니다

zkSNARK는 영지식 증명을 만드는 방법입니다. 특히, 영지식 증명을 생성하기 위한 간결하고 비대화형 방법입니다.

DAOrayaki DAO 리서치 보너스 풀:

펀딩 주소: DAOrayaki.eth

DAOrayaki DAO 리서치 보너스 풀:

펀딩 주소: DAOrayaki.eth

투표 진행: DAO 위원회 2/0 통과

연구 유형: 블록체인 영지식증명

zkSNARK는 영지식 증명을 만드는 방법입니다. 특히, 영지식 증명을 생성하기 위한 간결하고 비대화형 방법입니다.

원작자: 코비 구르칸

zkSNARK는 영지식 증명을 만드는 방법입니다. 특히, 영지식 증명을 생성하기 위한 간결하고 비대화형 방법입니다.

https://z.cash/technology/zksnarks/

zkSNARK가 정확히 무엇인지는 다음을 참조할 수 있습니다.

1. Zcash에서 zkSNARK를 구축하는 방법 - Zcash 팀 제공.

https://qed-it.com/trustless-computing-on-private-data/

2. 개인 데이터를 위한 신뢰할 수 없는 컴퓨팅 - Daniel Benarroch 및 Aviv Zohar, QED-it의 수석 암호 작성자

교수님 블로그 글입니다.

https://qed-it.com/2017/07/04/zkp-in-action/

3. 증명, 블록체인. ZKPinAction - ZKP를 설명하고 Sudoku용 ZKP 생성 방법을 설명하는 세션입니다.

https://qed-it.com/2017-12-20-the-incredible-machine/

동영상.

https://qed-it.com/2017/07/11/the-hunting-of-the-snark/

4. The Incredible Machine - 믿을 수 있는 설정을 설명하는 QED-it의 수석 과학자인 Aviv Zohar 교수의 블로그 게시물입니다.

5. SNARK 사냥 - ZKP를 실험하기 위한 일련의 수수께끼입니다.

QED-it에서는 zkSNARK 및 기타 도구를 사용하여 기업을 위한 영지식 블록체인을 만듭니다.

아마도 가장 잘 알려진 zkSNARK의 생산 배치는 ZCash일 것입니다. 이는 연결 불가능한 트랜잭션과 숨겨진 금액이 있는 암호화폐입니다. ZCash와 zkSNARK를 사용하는 일부 다른 제품은 Pinnochio라는 구조를 기반으로 하지만 더 구체적으로는 BCTV14a입니다. 예상하셨겠지만 놀라운 기술입니다. 이 구조에는 명백한 단점이 있습니다. 즉, 신뢰할 수 있는 설정입니다."신뢰할 수 있는 설정"설정은 CRS(공통 참조 문자열)를 생성하는 프로세스 또는 인증 및 확인 키 쌍으로 더 널리 알려져 있습니다. 이것들

열쇠"증명자와 검증자는 각각 특정 문제(또는 제약 시스템)의 증명을 생성하고 확인하는 데 사용됩니다."이 과정에서 일부 무작위 요소가 샘플링되지만 비밀로 유지되어야 합니다. 검증자가 이를 안다면 증명 프로세스에서 문제에 대한 실제 솔루션을 사용하지 않고도 성공적으로 검증된 증명을 만들 수 있기 때문입니다. 즉, 증거를 위조하고 건전성을 훼손하는 것입니다. 이 무작위성은 다음과 같이 알려져 있습니다.

. 단일 엔터티를 신뢰하지 않음으로써 이러한 우려를 피할 수 있는 방법이 있습니다. 공용 회로의 경우 이러한 방법은 일반적으로 여러 참가자가 나중에 파괴되는 임의성을 기부하는 다자간 계산을 포함합니다. 흥미롭게도 한 참가자가 정직하고 무작위성이 파괴되는 한 전체 프로세스는 안전합니다.

1. "The Ceremony "팟캐스트

https://www.wnycstudios.org/podcasts/radiolab/articles/ceremony

MPC를 사용하는 신뢰할 수 있는 설정의 몇 가지 주목할만한 예는 여전히 다음과 같습니다. ZCash.

https://z.cash.foundation/blog/powers-of-tau/

팟캐스트"Tau"2. 타우의 힘

여기 팝업이 표시될 수 있습니다.

...타우의 비밀은 매우 중요합니다. Tau가 증명자에게 알려지면 증명을 위조하기가 쉽습니다.

인증서를 생성

BCTV14a에서 제안한 구성을 간단히 살펴보겠습니다."이것은 수학 문제이므로 이 문서와 관련된 세부 정보를 선택해 보겠습니다."1. Tau는 설정 중에 무작위로 그려진 유한 필드의 점이며

유독성 폐기물"a*b=c "그것의 일부."a*b-c=0"。

2. 증명하는 동안 검증자는 제약 시스템의 솔루션과 공개 및 비공개 입력에서 A(z), B(z) 및 C(z)와 같은 일부 다항식을 계산합니다. 기본적으로 이러한 다항식은 다음을 나타냅니다."형태의 제약, 또는 동등"H(z)--H(Tau)。

3. 검증자는 또한 H(z)=(A(z)B(z)-C(z))/Z(z)를 계산합니다. 여기서 Z(z)는 제약 시스템을 0으로 나타내는 지점에서의 공용 다항식입니다. A, B, C는 검증자의 입력을 고려하므로 H는 분자도 같은 지점에서 0인 경우에만 계산할 수 있으며, 이는 검증자가 A*BC =0을 생성하는 문제에 대한 솔루션을 실제로 알고 있음을 증명합니다. . 이제 중요한 부분이 발생합니다. Tau를 몰라도 검증자는 다음을 계산할 수 있습니다.

색인 내

우리는 왜 이것을 하는가? 임의의 지점 Tau에서 평가함으로써 증명자는 방정식 H=(A*BC)/Z가 모든 Z에 대해 유지됨을 보여줄 확률이 높습니다. 같은 문제에 대해 다른 관점에서 보면, 증명자는 타우를 알지 못하고 높은 확률로 그 시점에서 정확히 같은 값을 산출하는 다항식을 생성할 수 없을 것입니다.

기술적으로 어떻게 해야 할까요? 설정 절차의 일부가 pk_Hi로 지정된 지수에 숨겨진 Tau의 모든 관련 거듭제곱을 포함하는 요소를 생성한다는 사실이 있습니다. H의 계수가 있는 경우 이를 결합하여 H(Tau)를 생성할 수 있습니다.

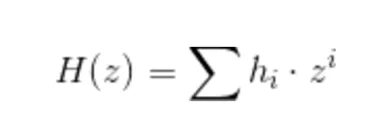
더 구체적으로

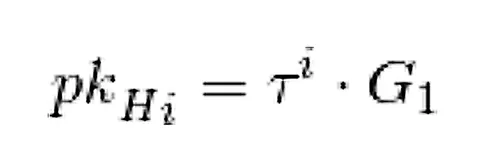
검증자가 계산한 H(z)

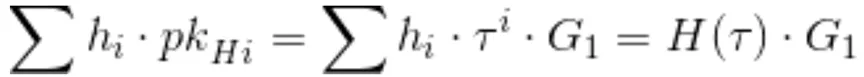
설정 중에 계산된 증명에서 가져온 키

H(Tau)의 "인트라 지수" 평가

증명을 받은 후 검증자는 검증자가 H=(A*BC)/Z 관계를 만족하는 H 계수를 실제로 제공했는지 여부를 지수에서 다시 확인할 수 있습니다. 검증자는 실제로 솔루션을 알고 있는 경우에만 수행할 수 있습니다.

위조된 증명서

이제 가설을 세워봅시다. 타우가 알려지면 어떻게 될까요? 어떤 이유로 설정 중에 노출되어 악의적인 검증자에게 알려진 경우.

분명히 증거를 위조하는 것은 매우 쉽습니다. H=(A*BC)/Z에 대한 동등성 검사가 특정 지점 Tau에서 수행되기 때문에 Tau에 대해 알고 있는 것을 사용하여 완전히 만족하는 다항식을 만들 수 있습니다. 즉, 항상 (A(Tau)*B(Tau)-C(Tau))/Z(Tau)를 반환하는 상수 다항식 H(z)를 만듭니다.

검사관의 검사가 통과되고 아무도 알 수 없습니다. 어렵게 들린다...

별말씀을요. Howard Wu의 libsnarktutorial을 기반으로 하는 이 개념 증명 코드를 확인하고 코드에 대한 수정 사항을 직접 확인하는 것을 환영합니다.

1. 프로그램은 C이지만 비트 분해를 위한 회로를 설정합니다.

3. 검증자는 디스크에서 Tau를 로드하고 잘못된 입력으로 증명합니다. Tau를 알고 있는 검증자는 입력에 관계없이 일정한 다항식을 생성합니다.