DAOrayaki DAO Research Bonus Pool:

Funding address: DAOrayaki.eth

DAOrayaki DAO Research Bonus Pool:

Funding address: DAOrayaki.eth

Voting progress: DAO Committee 2/0 passed

Total bounty: 60 USDC

Research Type: Blockchain Zero Knowledge Proofs

Original Author: Kobi Gurkan

zkSNARKs are a way to create zero-knowledge proofs. Specifically, concise, non-interactive methods for creating zero-knowledge proofs.

https://z.cash/technology/zksnarks/

What exactly is zkSNARKs can refer to the following

1. How zkSNARKs are built in Zcash - courtesy of the Zcash team.

https://qed-it.com/trustless-computing-on-private-data/

2. Trustless Computing for Private Data - Daniel Benarroch and Aviv Zohar, Chief Cryptographers at QED-it

Professor's blog post.

https://qed-it.com/2017/07/04/zkp-in-action/

3. Proof, blockchain. ZKPinAction - A session explaining ZKPs and how to create one for Sudoku

https://qed-it.com/2017-12-20-the-incredible-machine/

video.

https://qed-it.com/2017/07/11/the-hunting-of-the-snark/

4. The Incredible Machine - A blog post by Prof. Aviv Zohar, Chief Scientist of QED-it, explaining the believable setup.

5. Hunting SNARKs - A series of riddles for experimenting with ZKPs.

At QED-it, we use zkSNARKs and other tools to create zero-knowledge blockchains for enterprises.

Probably the best known production deployment of zkSNARKs is ZCash - a cryptocurrency with unlinkable transactions and hidden amounts. ZCash, as well as some other products utilizing zkSNARKs, are based on a structure called Pinnochio, although more specifically BCTV14a. It's an amazing piece of technology, as you might have suspected. This structure has an obvious disadvantage: the trusted setup."trusted settings"Setup is the process of generating a CRS (Common Reference String), or more publicly known as a pair of certification and verification keys. These

key"The prover and verifier are used to generate and verify proofs of a particular problem (or constraint system), respectively."During this process, some random elements are sampled but must be kept secret. Because if verifiers knew this, they would be able to create proofs that were successfully verified without using the actual solution to the problem in the proof process. In other words, to falsify proofs and undermine soundness. This randomness is also known as

. There are ways to avoid this concern by not placing trust in a single entity. For public circuits, these methods usually involve multi-party computation, in which multiple participants donate their randomness, which is later destroyed. Interestingly, as long as one participant is honest and their randomness is destroyed, the whole process is safe.

1. "The Ceremony "podcast

https://www.wnycstudios.org/podcasts/radiolab/articles/ceremony

Some notable examples of trusted setups using MPC are still: ZCash.

https://z.cash.foundation/blog/powers-of-tau/

podcast"Tau"2. Power of Tau

You might notice this popping up here

...Tau's secrecy is very important. Once Tau is known to the prover, it is easy to forge the proof.

create a certificate

Let's take a quick look at the construction proposed in BCTV14a."This is a math problem, so let's pick out the details that are relevant to this article:"1. Tau is a point in a finite field drawn randomly during setup and is

toxic waste"a*b=c "part of it."a*b-c=0"。

2. During the proof, the verifier computes some polynomials - A(z), B(z) and C(z) from the solution of the constraint system and public and private inputs. Essentially, these polynomials represent"constraints of the form, or equivalently"H(z)--H(Tau)。

3. The verifier also computes H(z)=(A(z)B(z)-C(z))/Z(z), where Z(z) is a public polynomial at points representing the constraint system to zero. Note that since A, B, and C take into account the verifier's input, H can only be computed if the numerator is also zeroed at the same point, proving that the verifier actually knows a solution to the problem that yields A*BC =0. The important part now happens - without knowing Tau, the verifier can calculate

within the index

Why do we do this? Because by evaluating at a random point Tau, the prover has a high probability of showing that the equation H=(A*BC)/Z holds for all Z. From a different perspective on the same problem, without knowing Tau, the prover, with high probability, will not be able to produce a polynomial that yields exactly the same value at that point.

How do we do this technically? There is the fact that part of the setup procedure produces elements containing all relevant powers of Tau hidden in the exponent, given as pk_Hi. If we have the coefficients of H, we can combine these and create H(Tau).

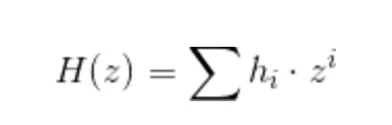
more specifically

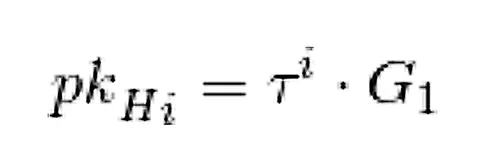
H(z) computed by the verifier

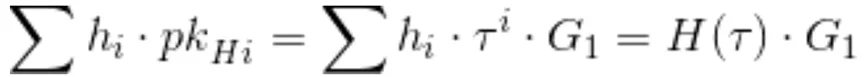
key taken from the attestation, computed during setup

"Intra-exponential" evaluation of H(Tau)

After receiving the proof, the verifier can check again in the exponent whether the verifier has indeed provided the coefficient of H satisfying the relationship H=(A*BC)/Z, which can only be done if the verifier actually knows a solution .

falsified certificate

Now let's make a hypothetical, what if Tau is known? If for some reason it was exposed during setup and known to a malicious validator.

Obviously, it is very easy to forge a proof. Because the equivalence check for H=(A*BC)/Z is done at a specific point Tau, we can use what we know about Tau to create a polynomial that satisfies fully. That is, create a constant polynomial H(z) that simply always returns (A(Tau)*B(Tau)-C(Tau))/Z(Tau).

The inspector's inspection will pass and no one will know. it sounds hard...

Not at all. You are more than welcome to check out this proof-of-concept code, based on Howard Wu's libsnarktutorial, and see for yourself the modifications made to the code.

1. The program sets up a circuit for bit decomposition, although it is C.

3. The verifier loads Tau from disk and proves with the wrong input. The verifier, knowing Tau, generates a constant polynomial regardless of the input.

in conclusion

The verifier then successfully verifies the proof!"in conclusion"I hope this post provides some insight into what everyone has been talking about about zkSNARKs