การวิเคราะห์เทคโนโลยีข้ามเครือข่ายสินทรัพย์ Bitcoin และ Layer2

ชื่อดั้งเดิม: ลายเซ็นอะแดปเตอร์และการประยุกต์ใช้กับ Cross-Chain Atomic Swaps

ลิงก์ต้นฉบับ: https://blog.bitlayer.org/Adaptor_Signatures_and_Its_Application_to_Cross-Chain_Atomic_Swaps/

ผู้เขียนต้นฉบับ: มูทูเรนด์, ลินเดลล์

1. บทนำ

ด้วยการพัฒนาอย่างรวดเร็วของแผนการขยายเลเยอร์ 2 ของ Bitcoin ความถี่ของการถ่ายโอนสินทรัพย์ข้ามเชนระหว่าง Bitcoin และเครือข่ายคู่เลเยอร์ 2 ได้เพิ่มขึ้นอย่างมาก แนวโน้มนี้ได้รับแรงผลักดันจากความสามารถในการปรับขนาดที่สูงขึ้น ค่าธรรมเนียมการทำธุรกรรมที่ลดลง และปริมาณงานที่สูงที่นำเสนอโดยเทคโนโลยีเลเยอร์ 2 เช่น Bitlayer ความก้าวหน้าเหล่านี้อำนวยความสะดวกในการทำธุรกรรมที่มีประสิทธิภาพและประหยัดมากขึ้น จึงส่งเสริมการยอมรับและบูรณาการ Bitcoin ในแอพพลิเคชั่นที่หลากหลายในวงกว้าง ด้วยเหตุนี้ การทำงานร่วมกันระหว่างเครือข่าย Bitcoin และเลเยอร์ 2 จึงกลายเป็นองค์ประกอบสำคัญของระบบนิเวศสกุลเงินดิจิทัล ขับเคลื่อนนวัตกรรม และมอบเครื่องมือทางการเงินที่หลากหลายและทรงพลังแก่ผู้ใช้

ดังที่แสดงในตารางที่ 1 มีโซลูชันทั่วไปสามโซลูชันสำหรับธุรกรรมข้ามสายโซ่ระหว่าง Bitcoin และเลเยอร์ 2 ได้แก่ ธุรกรรมข้ามสายโซ่แบบรวมศูนย์ สะพานข้ามสายโซ่ BitVM และการแลกเปลี่ยนอะตอมแบบข้ามสายโซ่ เทคโนโลยีทั้งสามนี้มีความแตกต่างกันในแง่ของสมมติฐานด้านความน่าเชื่อถือ ความปลอดภัย ความสะดวก ขีดจำกัดในการทำธุรกรรม ฯลฯ และสามารถตอบสนองความต้องการของแอปพลิเคชันที่แตกต่างกันได้

ตารางที่ 1. การเปรียบเทียบเทคโนโลยีธุรกรรมข้ามสายโซ่

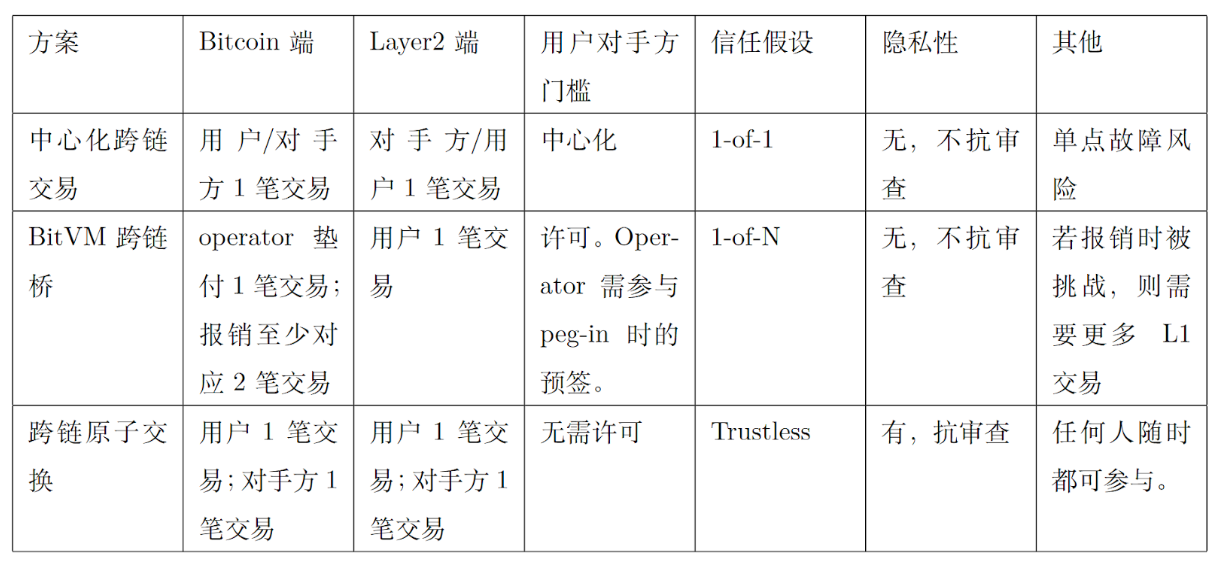
ธุรกรรมข้ามเครือข่ายแบบรวมศูนย์: ผู้ใช้ชำระเงิน Bitcoin ให้กับสถาบันแบบรวมศูนย์ก่อน (เช่น ฝ่ายโครงการหรือการแลกเปลี่ยน) จากนั้นสถาบันแบบรวมศูนย์จะจ่ายสินทรัพย์ที่มีมูลค่าเท่ากันไปยังที่อยู่ที่กำหนดโดยผู้ใช้บนเครือข่ายเลเยอร์ 2 ดังนั้น เสร็จสิ้นการโอนธุรกรรมสินทรัพย์ข้ามสายโซ่ ข้อดีของเทคโนโลยีนี้คือรวดเร็วและกระบวนการจับคู่ค่อนข้างง่ายเนื่องจากสถาบันแบบรวมศูนย์สามารถยืนยันและประมวลผลธุรกรรมได้อย่างรวดเร็ว อย่างไรก็ตาม ความปลอดภัยของวิธีการนี้ขึ้นอยู่กับความน่าเชื่อถือและความน่าเชื่อถือของสถาบันแบบรวมศูนย์ทั้งหมด หากสถาบันแบบรวมศูนย์พบกับความล้มเหลวทางเทคนิค การโจมตีที่เป็นอันตราย หรือการผิดนัด เงินทุนของผู้ใช้จะเผชิญกับความเสี่ยงที่สูงขึ้น นอกจากนี้ ธุรกรรมข้ามเครือข่ายแบบรวมศูนย์อาจทำให้ความเป็นส่วนตัวของผู้ใช้รั่วไหล และผู้ใช้จำเป็นต้องพิจารณาอย่างรอบคอบเมื่อเลือกวิธีนี้ ดังนั้น แม้ว่าความสะดวกและประสิทธิภาพจะมอบความสะดวกสบายให้กับผู้ใช้ แต่ความปลอดภัยและความไว้วางใจถือเป็นความท้าทายหลักที่ธุรกรรมข้ามเครือข่ายแบบรวมศูนย์ต้องเผชิญ

สะพานข้ามสายโซ่ BitVM: เทคโนโลยีนี้ค่อนข้างซับซ้อน ขั้นแรก ในระยะ Peg-in ผู้ใช้จ่าย Bitcoin ไปยังที่อยู่ที่มีลายเซ็นหลายลายเซ็นซึ่งควบคุมโดย BitVM Alliance เพื่อล็อค Bitcoin จำนวนโทเค็นที่สอดคล้องกันจะถูกสร้างในเลเยอร์ 2 และโทเค็นจะถูกใช้เพื่อใช้ธุรกรรมและแอปพลิเคชันของเลเยอร์ 2 เมื่อผู้ใช้ทำลายโทเค็นเลเยอร์ 2 ผู้ดำเนินการจะชำระเงินล่วงหน้า ต่อจากนั้น ผู้ดำเนินการจะคืนเงินตามจำนวน Bitcoins ที่สอดคล้องกันในกลุ่มลายเซ็นหลายลายเซ็นที่ควบคุมโดย BitVM Alliance เพื่อป้องกันไม่ให้ผู้ปฏิบัติงานทำสิ่งชั่วร้าย กระบวนการคืนเงินจะใช้กลไกท้าทายเชิงบวก กล่าวคือ บุคคลที่สามสามารถท้าทายพฤติกรรมการจ่ายคืนที่เป็นอันตรายและขัดขวางพฤติกรรมที่ชั่วร้ายได้ เทคโนโลยีนี้นำเสนอกลไกความท้าทายในแง่ดี ดังนั้นเทคโนโลยีจึงค่อนข้างซับซ้อน นอกจากนี้ กลไกการท้าทายในแง่ดียังเกี่ยวข้องกับธุรกรรมการท้าทายและการตอบโต้จำนวนมาก โดยมีค่าธรรมเนียมการทำธุรกรรมที่สูงขึ้น ดังนั้น สะพานข้ามสายโซ่ BitVM จึงเหมาะสำหรับธุรกรรมที่มีขนาดใหญ่มากเท่านั้น ซึ่งคล้ายกับการออก U เพิ่มเติม และจึงมีการใช้งานน้อยลง

Cross-chain Atomic Swap: Atomic swap เป็นสัญญาที่ช่วยให้สามารถซื้อขายสกุลเงินดิจิตอลแบบกระจายอำนาจได้ ในกรณีนี้ "อะตอมมิก" หมายความว่าการเปลี่ยนแปลงความเป็นเจ้าของเนื้อหาหนึ่งหมายถึงการเปลี่ยนแปลงความเป็นเจ้าของเนื้อหาอื่นอย่างแท้จริง แนวคิดนี้ถูกเสนอครั้งแรกในปี 2013 โดย TierNolan ในฟอรัม Bitcointalk เป็นเวลาสี่ทศวรรษแล้วที่การแลกเปลี่ยนอะตอมยังคงอยู่ในขอบเขตของทฤษฎี จนกระทั่งปี 2017 Decred และ Litecoin กลายเป็นระบบบล็อกเชนระบบแรกที่ประสบความสำเร็จในการแลกเปลี่ยนอะตอมมิก Atomic swaps ต้องเกี่ยวข้องกับสองฝ่าย และไม่มีบุคคลที่สามใดสามารถขัดขวางหรือแทรกแซงกระบวนการแลกเปลี่ยนได้ ซึ่งหมายความว่าเทคโนโลยีนี้มีการกระจายอำนาจ ไม่เซ็นเซอร์ มีการป้องกันความเป็นส่วนตัวที่ดี และสามารถบรรลุธุรกรรมข้ามสายโซ่ความถี่สูงได้ จึงมีการใช้กันอย่างแพร่หลายในการแลกเปลี่ยนแบบกระจายอำนาจ ปัจจุบัน cross-chain atomic swap ต้องใช้ธุรกรรม 4 รายการ โซลูชันบางอย่าง พยายามบีบอัดจำนวนธุรกรรมให้เป็น 2 รายการ แต่การทำเช่นนี้จะเพิ่มข้อกำหนดออนไลน์แบบเรียลไทม์สำหรับทั้งสองฝ่ายในการแลกเปลี่ยน สุดท้ายนี้ เทคโนโลยี cross-chain atomic swap ส่วนใหญ่จะมีการล็อคเวลาแฮชและลายเซ็นของอแด็ปเตอร์

Cross-chain atomic swap ขึ้นอยู่กับ Hash Time Lock (HTLC): โปรเจ็กต์แรกที่ใช้ cross-chain atomic swap ได้สำเร็จคือ Decred ซึ่งใช้ "hash lock" และ "time lock" เพื่อให้บรรลุผลสำเร็จด้วยความช่วยเหลือของสคริปต์ on-chain (หรือสัญญาอัจฉริยะ) การแลกเปลี่ยนอะตอมมิกที่เสนอโดย TierNolan HTLC อนุญาตให้ผู้ใช้สองคนทำธุรกรรมสกุลเงินดิจิทัลแบบจำกัดเวลา เช่น ผู้รับต้องส่งหลักฐานการเข้ารหัส ("ความลับ") ไปยังสัญญาภายในระยะเวลาที่กำหนด (กำหนดโดยหมายเลขบล็อกหรือความสูงของบล็อก) มิฉะนั้นเงินจะถูกส่งกลับไปยัง ผู้ส่งโดย. หากผู้รับยืนยันการชำระเงิน การทำธุรกรรมจะสำเร็จ ดังนั้น บล็อกเชนที่เข้าร่วมทั้งสองรายการจำเป็นต้องมีฟังก์ชัน "แฮชล็อค" และ "ล็อคเวลา"

แม้ว่าการแลกเปลี่ยนอะตอมมิก HTLC จะเป็นความก้าวหน้าครั้งสำคัญในด้านเทคโนโลยีการแลกเปลี่ยนแบบกระจายอำนาจ แต่ก็มีปัญหาดังต่อไปนี้ ธุรกรรม atomic swap และข้อมูลที่เกี่ยวข้องนั้นดำเนินการแบบออนไลน์ ส่งผลให้ความเป็นส่วนตัวของผู้ใช้รั่วไหล กล่าวอีกนัยหนึ่ง ทุกครั้งที่มีการแลกเปลี่ยน แฮชเดียวกันจะปรากฏบนบล็อกเชนทั้งสอง โดยคั่นด้วยบล็อกเพียงไม่กี่บล็อก ซึ่งหมายความว่าผู้สังเกตการณ์สามารถเชื่อมโยงสกุลเงินที่เข้าร่วมในการแลกเปลี่ยนได้ เช่น ค้นหาค่าแฮชเดียวกันในบล็อกที่อยู่ใกล้กัน (ตามการประทับเวลา) เมื่อติดตามสกุลเงินข้ามเครือข่าย การระบุแหล่งที่มาเป็นเรื่องง่าย แม้ว่าการวิเคราะห์นี้จะไม่เปิดเผยข้อมูลระบุตัวตนที่เกี่ยวข้องใดๆ แต่บุคคลที่สามสามารถอนุมานตัวตนของผู้แสดงที่เกี่ยวข้องได้อย่างง่ายดาย

การแลกเปลี่ยนอะตอมแบบข้ามสายโซ่ตามลายเซ็นของอะแดปเตอร์: การแลกเปลี่ยนประเภทที่สองที่นำเสนอโดย BasicSwap เรียกว่าการแลกเปลี่ยนอะตอมมิกแบบ "ลายเซ็นอะแดปเตอร์" อ้างอิงจากบทความที่ตีพิมพ์โดยนักพัฒนา Monero Joël Gugger ในปี 2020 ในหัวข้อ “ Bitcoin–Monero Cross-chain Atomic Swap }"กระดาษ. เอกสารนี้สามารถกล่าวได้ว่าเป็นการนำเอกสาร One-Time Verifiable Encrypted Signatures, AKA Adapter Signatures ของ Lloyd Fournier มาใช้ในปี 2019 ลายเซ็นอะแดปเตอร์เป็นลายเซ็นเพิ่มเติมที่รวมกับลายเซ็นเริ่มต้นเพื่อเปิดเผยข้อมูลลับ ช่วยให้ทั้งสองฝ่ายสามารถเปิดเผยข้อมูลทั้งสองส่วนพร้อมกัน และเป็นองค์ประกอบสำคัญของโปรโตคอลแบบไร้สคริปต์ที่ทำให้คู่การแลกเปลี่ยนอะตอมมิกของ Monero เป็นไปได้

เมื่อเปรียบเทียบกับ HTLC atomic swaps การแลกเปลี่ยนอะตอมมิกตามลายเซ็นของอะแดปเตอร์มีข้อดี 3 ประการ: ประการแรก รูปแบบการแลกเปลี่ยนลายเซ็นของอะแดปเตอร์จะแทนที่สคริปต์ออนไลน์ที่การแลกเปลี่ยน "แฮชลับ" อาศัย รวมถึงการล็อคเวลาและการล็อคแฮช กล่าวอีกนัยหนึ่ง ข้อมูลลับและแฮชที่เป็นความลับในการแลกเปลี่ยน HTLC ไม่มีการติดต่อโดยตรงในการแลกเปลี่ยนลายเซ็นของอะแดปเตอร์ ดังนั้นจึงเรียกว่า "สคริปต์ไร้สคริปต์" ในชุมชนการวิจัย Bitcoin นอกจากนี้ เนื่องจากไม่มีสคริปต์ดังกล่าวเข้ามาเกี่ยวข้อง พื้นที่บนเชนจึงลดลง ทำให้การสลับอะตอมมิกตามลายเซ็นของอะแดปเตอร์มีน้ำหนักเบาและราคาถูกกว่า สุดท้ายนี้ HTLC กำหนดให้แต่ละเชนใช้ค่าแฮชเดียวกัน และธุรกรรมที่เกี่ยวข้องกับการแลกเปลี่ยนอะตอมมิกที่ลงนามด้วยอะแดปเตอร์ไม่สามารถเชื่อมโยงได้ จึงบรรลุการคุ้มครองความเป็นส่วนตัว

บทความนี้จะแนะนำหลักการของลายเซ็นอะแดปเตอร์ Schnorr/ECDSA และการแลกเปลี่ยนอะตอมมิกแบบข้ามสายโซ่เป็นอันดับแรก จากนั้น จะวิเคราะห์ปัญหาด้านความปลอดภัยของตัวเลขสุ่มในลายเซ็นของอะแดปเตอร์ และปัญหาความแตกต่างของระบบและความแตกต่างของอัลกอริทึมในสถานการณ์แบบข้ามสายโซ่ และให้แนวทางแก้ไข สุดท้ายนี้ ลายเซ็นของอะแดปเตอร์จะถูกขยายและนำไปใช้เพื่อให้เกิดการดูแลสินทรัพย์ดิจิทัลแบบไม่โต้ตอบ

2. ลายเซ็นอะแดปเตอร์และการแลกเปลี่ยนอะตอมแบบข้ามสายโซ่

2.1 ลายเซ็นอะแดปเตอร์ Schnorr และการแลกเปลี่ยนอะตอมมิก

2.2 ลายเซ็นอะแดปเตอร์ ECDSA และการแลกเปลี่ยนอะตอมมิก

2.2.1 การพิสูจน์ความรู้เป็นศูนย์ zk{v |.

3. ปัญหาด้านความปลอดภัยและแนวทางแก้ไข

3.1 ปัญหาและวิธีแก้ปัญหาจำนวนสุ่ม

3.1.1 ปัญหาการรั่วไหลของเลขสุ่ม

ลายเซ็นล่วงหน้าที่ลงนามโดยอะแดปเตอร์ Schnorr/ECDSA ทั้งหมดกำหนดให้เป็นตัวเลขสุ่ม $r$ Œ = r ᐧ G นอกจากนี้ การพิสูจน์ความรู้เป็นศูนย์จะมอบตัวเลขสุ่ม $v$ ไปยัง $Ṽ=v ᐧ G, V=v ᐧ Y$ หากตัวเลขสุ่มรั่วไหล รหัสส่วนตัวก็จะรั่วไหล

โดยเฉพาะในโปรโตคอล Schnorr หากตัวเลขสุ่ม $r$ รั่วไหล ก็สามารถคำนวณได้ตามสมการ

$ŝ = r + c x.$

คำนวณคีย์ส่วนตัว $x$

ในทำนองเดียวกัน ในโปรโตคอล ECDSA หากตัวเลขสุ่ม $r$ รั่วไหล ก็คำนวณได้ตามสมการ

$ŝ = r^{-1 }(แฮช(m)+R_x x).$

คำนวณคีย์ส่วนตัวเพื่อรับ $x$

ในที่สุด ในโปรโตคอลการพิสูจน์ความรู้เป็นศูนย์ หากตัวเลขสุ่ม $v$ รั่วไหล ก็สามารถกำหนดได้ตามสมการ

$z := v + c r.$

คำนวณตัวเลขสุ่ม $r$ และคำนวณคีย์ส่วนตัว $x$ เพิ่มเติมตามตัวเลขสุ่ม $r$ ดังนั้นจึงต้องลบเลขสุ่มทันทีหลังใช้งาน

3.1.2 ปัญหาการใช้ตัวเลขสุ่มซ้ำ

สำหรับธุรกรรมข้ามสายโซ่สองรายการใดๆ หากโปรโตคอลลายเซ็นของอะแดปเตอร์ใช้หมายเลขสุ่มเดียวกัน รหัสส่วนตัวจะรั่วไหล โดยเฉพาะอย่างยิ่ง ในโปรโตคอล Schnorr หากใช้ตัวเลขสุ่ม $r$ เดียวกัน จะไม่ทราบเพียง $r$ และ $x$ ในระบบสมการต่อไปนี้

$ŝ_ 1 =r + c_ 1 x, $

$ ŝ_ 2 = r + c_ 2 x

ดังนั้น ระบบสมการจึงสามารถแก้ได้เพื่อให้ได้คีย์ส่วนตัว $x$

ในทำนองเดียวกัน ในโปรโตคอลลายเซ็นอะแด็ปเตอร์ ECDSA หากใช้ตัวเลขสุ่ม $r$ เดียวกัน จะไม่ทราบเฉพาะ $r$ และ $x$ ในระบบสมการต่อไปนี้

$ ŝ_ 1 = r^{-1 }(แฮช(m_ 1)+R_x x),$

$ ŝ_ 2 = r^{-1 }(แฮช(m_ 2)+R_x x).$

ดังนั้น ระบบสมการจึงสามารถแก้ได้เพื่อให้ได้คีย์ส่วนตัว $x$

สุดท้ายนี้ ในโปรโตคอลพิสูจน์ความรู้เป็นศูนย์ ถ้าใช้ตัวเลขสุ่ม $v$ เดียวกัน จะไม่ทราบเพียง $v$ และ $r$ เท่านั้นในระบบสมการต่อไปนี้

$z_ 1 = v+c_ 1 r, $

$ z_ 2 = v+c_ 2 ร

ดังนั้น ระบบสมการจึงสามารถแก้ได้เพื่อให้ได้ตัวเลขสุ่ม $r$ และระบบสมการสามารถแก้เพิ่มเติมเพื่อให้ได้คีย์ส่วนตัว $x$

โดยการเปรียบเทียบ หากผู้ใช้ที่แตกต่างกันใช้หมายเลขสุ่มเดียวกัน รหัสส่วนตัวก็จะรั่วไหลเช่นกัน กล่าวอีกนัยหนึ่ง ผู้ใช้สองคนที่ใช้ตัวเลขสุ่มเดียวกันสามารถแก้ระบบสมการและรับรหัสส่วนตัวของกันและกันได้ ดังนั้น RFC 6979 จึงควรใช้เพื่อจัดการกับการนำตัวเลขสุ่มกลับมาใช้ใหม่

3.1.3 วิธีแก้ปัญหา: RFC 6979

RFC 6979 ระบุวิธีการสร้างลายเซ็นดิจิทัลที่กำหนดโดยใช้ DSA และ ECDSA เพื่อแก้ไขปัญหาด้านความปลอดภัยที่เกี่ยวข้องกับการสร้างค่าสุ่ม k ลายเซ็น DSA และ ECDSA แบบดั้งเดิมอาศัยตัวเลขสุ่ม k ที่สร้างขึ้นแบบสุ่มสำหรับการดำเนินการลงนามแต่ละครั้ง หากหมายเลขสุ่มนี้ถูกนำมาใช้ซ้ำหรือสร้างขึ้นอย่างไม่เหมาะสม ความปลอดภัยของคีย์ส่วนตัวอาจถูกบุกรุกได้ RFC 6979 ขจัดความจำเป็นในการสร้างตัวเลขสุ่มโดยรับ $k$ จากคีย์ส่วนตัวและข้อความที่จะลงนามตามที่กำหนด สิ่งนี้ทำให้แน่ใจได้ว่าเมื่อมีการเซ็นข้อความเดียวกันด้วยคีย์ส่วนตัวเดียวกัน ลายเซ็นจะเหมือนกันเสมอ ช่วยเพิ่มความสามารถในการทำซ้ำและคาดเดาได้ โดยเฉพาะอย่างยิ่ง $k$ ที่กำหนดถูกสร้างขึ้นโดย HMAC กระบวนการนี้เกี่ยวข้องกับการแฮชคีย์ส่วนตัว ข้อความ และตัวนับด้วยฟังก์ชันแฮช (เช่น SHA 256)

$k = SHA 256(sk, msg, counter).$

ในสมการข้างต้น เพื่อความง่ายในการแสดงออก ค่าแฮชจะถูกคำนวณเฉพาะคีย์ส่วนตัว sk, ข้อความ msg และตัวนับตัวนับเท่านั้น ที่จริงแล้ว กระบวนการคำนวณใน RFC 6979 เกี่ยวข้องกับการคำนวณแฮชที่มากกว่า สมการนี้ทำให้แน่ใจได้ว่า k จะไม่ซ้ำกันสำหรับแต่ละข้อความ ในขณะที่สามารถทำซ้ำได้สำหรับอินพุตเดียวกัน และลดความเสี่ยงของการเปิดเผยคีย์ส่วนตัวที่เกี่ยวข้องกับตัวสร้างตัวเลขสุ่มที่อ่อนแอหรือเสียหาย ดังนั้น RFC 6979 จึงจัดเตรียมเฟรมเวิร์กที่มีประสิทธิภาพสำหรับลายเซ็นดิจิทัลที่กำหนดได้โดยใช้ DSA และ ECDSA จัดการปัญหาด้านความปลอดภัยที่สำคัญที่เกี่ยวข้องกับการสร้างตัวเลขสุ่ม และปรับปรุงความน่าเชื่อถือและความสามารถในการคาดการณ์ของลายเซ็นดิจิทัล ทำให้เป็นมาตรฐานอันมีค่าสำหรับแอปพลิเคชันที่ต้องการความปลอดภัยสูงและปฏิบัติตามข้อกำหนดการปฏิบัติงานที่เข้มงวด ลายเซ็น Schnorr/ECDSA มีข้อบกพร่องด้านตัวเลขสุ่ม และจำเป็นต้องป้องกันโดยใช้ RFC 6979 ดังนั้น การเซ็นชื่ออะแดปเตอร์ที่ใช้ Schnorr/ECDSA ยังมีปัญหาเหล่านี้ และจำเป็นต้องใช้ข้อกำหนด RFC 6979 เพื่อแก้ไขปัญหาเหล่านี้

3.2 ปัญหาและแนวทางแก้ไขสถานการณ์ข้ามสายโซ่

3.2.1 UTXO และระบบแบบจำลองบัญชีปัญหาและแนวทางแก้ไขที่แตกต่างกัน

ดังที่แสดงในรูปที่ 1 Bitcoin ใช้โมเดล UTXO เพื่อใช้ลายเซ็น ECDSA ดั้งเดิมโดยอิงตามเส้นโค้ง Secp 256 k 1 Bitlayer เป็น EVM ที่เข้ากันได้กับเครือข่าย Bitcoin L2 ใช้เส้นโค้ง Secp 256 k 1 และรองรับลายเซ็น ECDSA ดั้งเดิม ลายเซ็นอะแดปเตอร์ใช้ตรรกะที่จำเป็นสำหรับการแลกเปลี่ยน BTC ในขณะที่การแลกเปลี่ยน Bitlayer นั้นขับเคลื่อนโดยพลังของสัญญาอัจฉริยะ Ethereum

การสลับอะตอมมิกแบบข้ามสายโซ่ตามลายเซ็นของอะแดปเตอร์ หรืออย่างน้อยรูปแบบลายเซ็นของอะแดปเตอร์แบบกึ่งไร้สคริปต์ที่ออกแบบมาเพื่อทำงานกับเส้นโค้ง ECDSA นั้นเข้ากันไม่ได้กับ Ethereum เหตุผลก็คือ Ethereum เป็นรูปแบบบัญชี ไม่ใช่โมเดล UTXO โดยเฉพาะอย่างยิ่ง การแลกเปลี่ยนอะตอมมิกตามลายเซ็นของอะแดปเตอร์กำหนดให้ธุรกรรมการคืนเงินต้องลงนามล่วงหน้า อย่างไรก็ตาม ในระบบ Ethereum ธุรกรรมไม่สามารถลงนามล่วงหน้าได้โดยไม่รู้ตัว ดังนั้นฝ่ายหนึ่งฝ่ายสามารถส่งธุรกรรมระหว่างการเสร็จสิ้นการลงนามล่วงหน้าและการดำเนินการของธุรกรรม ซึ่งจะทำให้ธุรกรรมที่ลงนามล่วงหน้าเป็นโมฆะ (เนื่องจาก nonce ถูกใช้ไปแล้วและไม่สามารถนำมาใช้ซ้ำได้)

นอกจากนี้ จากมุมมองความเป็นส่วนตัว ซึ่งหมายความว่าการไม่เปิดเผยตัวตนของการแลกเปลี่ยน Bitlayer นั้นดีกว่า HTLC (สัญญาสามารถพบได้ทั้งสองด้านของการแลกเปลี่ยน) อย่างไรก็ตาม ความจำเป็นที่ฝ่ายหนึ่งฝ่ายใดจะต้องมีสัญญาสาธารณะทำให้การแลกเปลี่ยน Bitlayer แบบไม่เปิดเผยตัวตนน้อยกว่าลายเซ็นของอะแดปเตอร์ ในด้านหนึ่งที่ไม่มีสัญญา ธุรกรรม Swap จะดูเหมือนธุรกรรมอื่นๆ อย่างไรก็ตาม ในด้านสัญญา EVM ธุรกรรมดังกล่าวมีไว้สำหรับการแลกเปลี่ยนสินทรัพย์อย่างชัดเจน แม้ว่าฝ่ายหนึ่งจะมีสัญญาสาธารณะ แต่ก็เป็นไปไม่ได้ที่จะติดตามกลับไปยังเชนอื่น แม้จะใช้เครื่องมือวิเคราะห์ลูกโซ่ที่ซับซ้อนก็ตาม

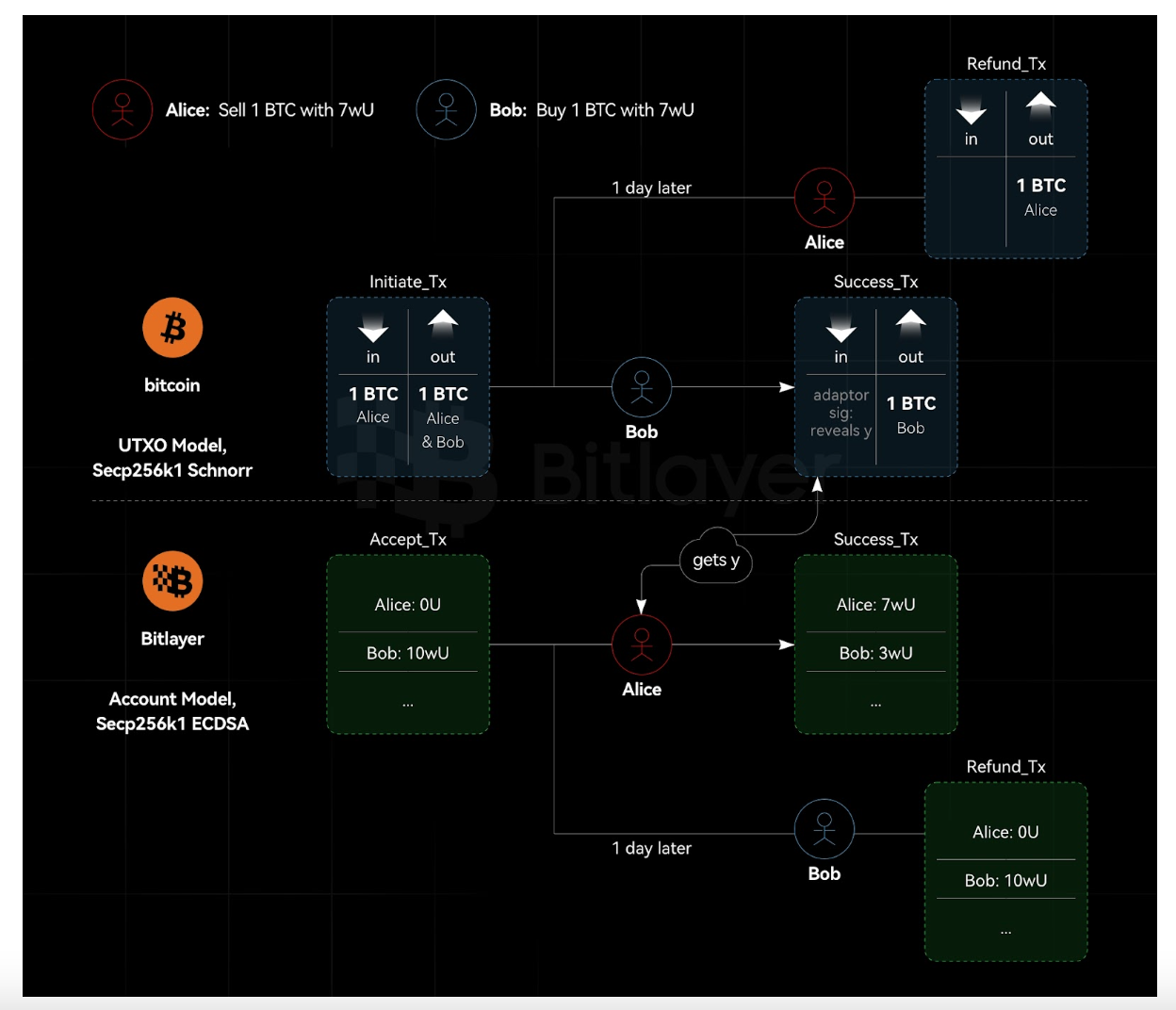
รูปที่ 1 UTXO และรูปแบบบัญชีระบบที่ต่างกันแบบ cross-chain atomic swap

ปัจจุบัน Bitlayer รองรับลายเซ็น ECDSA ดั้งเดิม และยังสามารถใช้การตรวจสอบลายเซ็น Schnorr ผ่านสัญญาอัจฉริยะได้อีกด้วย หากคุณใช้ธุรกรรม Bitlayer แบบเนทีฟ คุณจะไม่สามารถลงนามล่วงหน้าในธุรกรรมการคืนเงินใน Atomic Swap ได้ คุณต้องใช้ธุรกรรม Bitlayer Smart Contract เพื่อให้บรรลุ Atomic Swap อย่างไรก็ตาม กระบวนการนี้จะเสียสละความเป็นส่วนตัว กล่าวคือ ธุรกรรมที่เข้าร่วมใน Atomic Swap ในระบบ Bitlayer นั้นสามารถตรวจสอบย้อนกลับได้ แต่ธุรกรรมในระบบ BTC ไม่สามารถติดตามได้ แอปพลิเคชัน Dapp เช่น Tornado Cash สามารถออกแบบบนฝั่ง Bitlayer เพื่อให้บริการความเป็นส่วนตัวสำหรับการทำธุรกรรมทางฝั่ง Bitlayer ใน BTC และ Bitlayer atomic swaps

3.2.2 เส้นโค้งเดียวกัน อัลกอริธึมต่างกัน ความปลอดภัยของลายเซ็นอแด็ปเตอร์

ดังที่แสดงในรูปที่ 2 สมมติว่าทั้ง Bitcoin และ Bitlayer ใช้เส้นโค้ง Secp 256 k 1 แต่ Bitcoin ใช้ลายเซ็น Schnorr และ Bitlayer ใช้ ECDSA ในกรณีนี้ ลายเซ็นของอะแดปเตอร์ที่ใช้ Schnorr และ ECDSA มีความปลอดภัยที่พิสูจน์ได้ สมมติว่ามอบออราเคิลลายเซ็น ECDSA และ Schnorr แล้ว เครื่องจำลอง S สามารถสร้างขึ้นเพื่อทำลาย ECDSA จากนั้นให้เฉพาะออราเคิลลายเซ็น ECDSA เท่านั้น เครื่องจำลอง S สามารถสร้างขึ้นเพื่อหยุด ECDSA อย่างไรก็ตาม ECDSA มีความปลอดภัย ในทำนองเดียวกัน สมมติว่ามอบออราเคิลลายเซ็น ECDSA และ Schnorr แล้ว เครื่องจำลอง S สามารถสร้างขึ้นเพื่อทำลายลายเซ็น Schnorr จากนั้นให้เฉพาะออราเคิลลายเซ็น ECDSA เท่านั้น เครื่องจำลอง S สามารถสร้างขึ้นเพื่อทำลายลายเซ็น Schnorr อย่างไรก็ตาม ลายเซ็น Schnorr มีความปลอดภัย ดังนั้น ในสถานการณ์แบบข้ามสายโซ่ ลายเซ็นของอะแด็ปเตอร์จะใช้เส้นโค้งเดียวกัน แต่มีอัลกอริธึมลายเซ็นที่แตกต่างกัน ซึ่งปลอดภัย กล่าวอีกนัยหนึ่ง การลงนามอะแดปเตอร์อนุญาตให้ปลายด้านหนึ่งใช้ ECDSA และปลายอีกด้านหนึ่งใช้การเซ็นชื่อ Schnorr

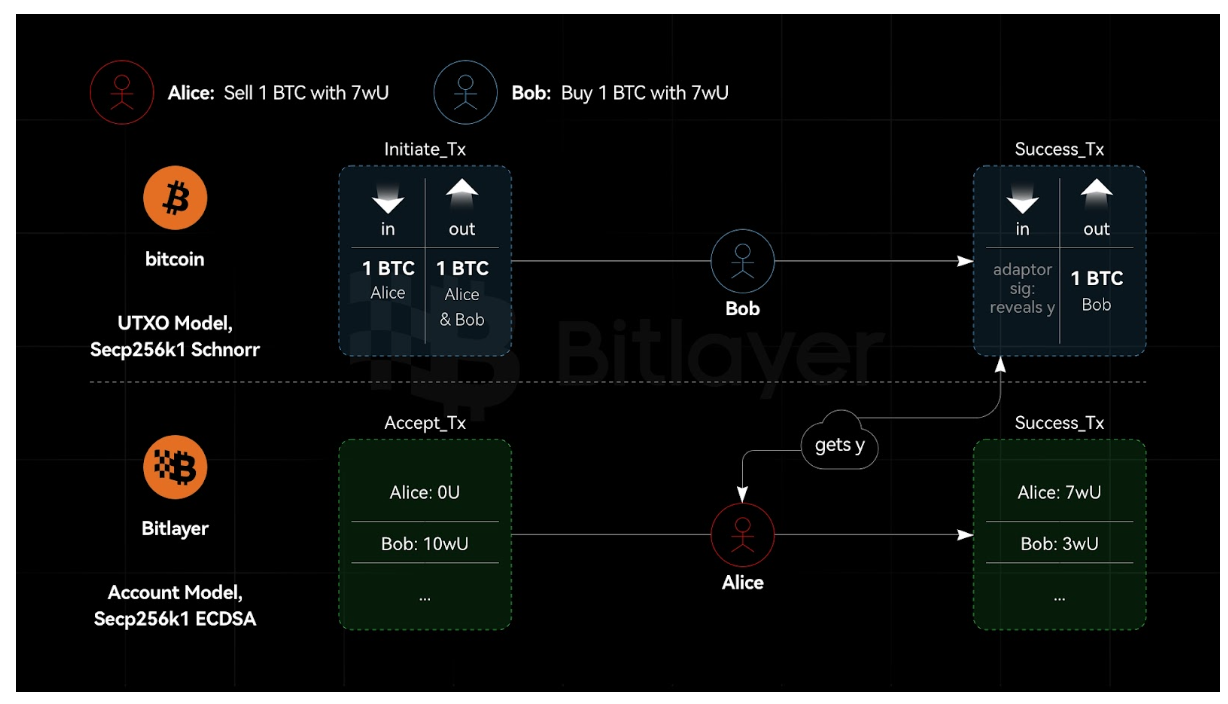
รูปที่ 2 เส้นโค้งเดียวกัน อัลกอริธึมต่างกัน ลายเซ็นของอแด็ปเตอร์

3.2.3 เส้นโค้งที่แตกต่างกัน ลายเซ็นของอะแดปเตอร์ไม่ปลอดภัย

สมมติว่า Bitcoin ใช้เส้นโค้ง Secp 256 k 1 และลายเซ็น ECDSA ในขณะที่ Bitlayer ใช้เส้นโค้ง ed 25519 และลายเซ็น Schnorr ในกรณีนี้ ไม่สามารถใช้ลายเซ็นอะแดปเตอร์ได้ เนื่องจากเส้นโค้งที่แตกต่างกัน ลำดับของกลุ่มเส้นโค้งวงรีจึงแตกต่างกัน กล่าวคือ ค่าสัมประสิทธิ์โมดูลจะแตกต่างกัน เมื่อ Bob ปรับ $y$ ให้เข้ากับลายเซ็น ECDSA ในระบบ Bitcoin เขาจะคำนวณ $s:= ŝ+y$ ในขณะนี้ สเปซค่าของ $y$ คือสเกลาร์สเปซของกลุ่มเส้นโค้งวงรี Secp 256 k 1 จากนั้น Alice จะต้องดำเนินการลายเซ็น Schnorr บนกลุ่มเส้นโค้งวงรี ed 25519 โดยใช้ $y$ อย่างไรก็ตาม โคแฟกเตอร์ของเส้นโค้ง ed 25519 คือ 8 และค่าสัมประสิทธิ์โมดูลไม่เท่ากับค่าสัมประสิทธิ์โมดูลของกลุ่มเส้นโค้งวงรี Secp 256 k 1 ดังนั้น การใช้ $y$ สำหรับลายเซ็น Schnorr บนเส้นโค้ง ed 25519 จึงไม่ปลอดภัย

4. การสมัครดูแลสินทรัพย์ดิจิทัล

มีผู้เข้าร่วมสามคนในการดูแลสินทรัพย์ดิจิทัล: ผู้ซื้อ Alice, ผู้ขาย Bob และผู้ดูแล การใช้ลายเซ็นอะแดปเตอร์ช่วยให้สามารถดูแลสินทรัพย์ดิจิทัลตามเกณฑ์แบบไม่โต้ตอบ และสร้างอินสแตนซ์ชุดย่อยของกลยุทธ์การใช้จ่ายตามเกณฑ์โดยไม่ต้องโต้ตอบ ชุดย่อยนี้ประกอบด้วยผู้เข้าร่วม 2 ประเภท: ผู้เข้าร่วมที่มีส่วนร่วมในการเตรียมใช้งานและผู้เข้าร่วมที่ไม่มีส่วนร่วมในการเตรียมใช้งาน ส่วนประเภทหลังเรียกว่าผู้ดูแล ผู้ดูแลไม่สามารถลงนามในธุรกรรมโดยพลการได้ และส่งเฉพาะความลับไปยังฝ่ายสนับสนุนฝ่ายใดฝ่ายหนึ่งเท่านั้น

ในแง่หนึ่ง ผู้ดูแลสามารถเลือกระหว่างธุรกรรมการชำระเงินคงที่เพียงไม่กี่รายการเท่านั้น และไม่สามารถลงนามในธุรกรรมใหม่กับฝ่ายใดฝ่ายหนึ่งได้ กลไกการเผยแพร่ที่เป็นความลับนี้จึงทำให้โฮสติ้งขีดจำกัดแบบไม่โต้ตอบมีความยืดหยุ่นน้อยกว่าลายเซ็น Schnorr ขีดจำกัด ในทางกลับกัน สามารถตั้งค่านโยบายการใช้จ่าย 2 ใน 3 ได้โดยใช้ลายเซ็น Schnorr ตามเกณฑ์ อย่างไรก็ตาม โปรโตคอลลายเซ็น Schnorr ตามเกณฑ์กำหนดให้มีบุคคลที่สามเพื่อเรียกใช้โปรโตคอลการสร้างคีย์แบบกระจายอำนาจ ดังนั้น โปรโตคอลเอสโครว์สินทรัพย์ตามลายเซ็นของอะแด็ปเตอร์จึงมีข้อดีของการไม่โต้ตอบ

4.1 การดูแลสินทรัพย์แบบไม่โต้ตอบตามลายเซ็นของอะแดปเตอร์

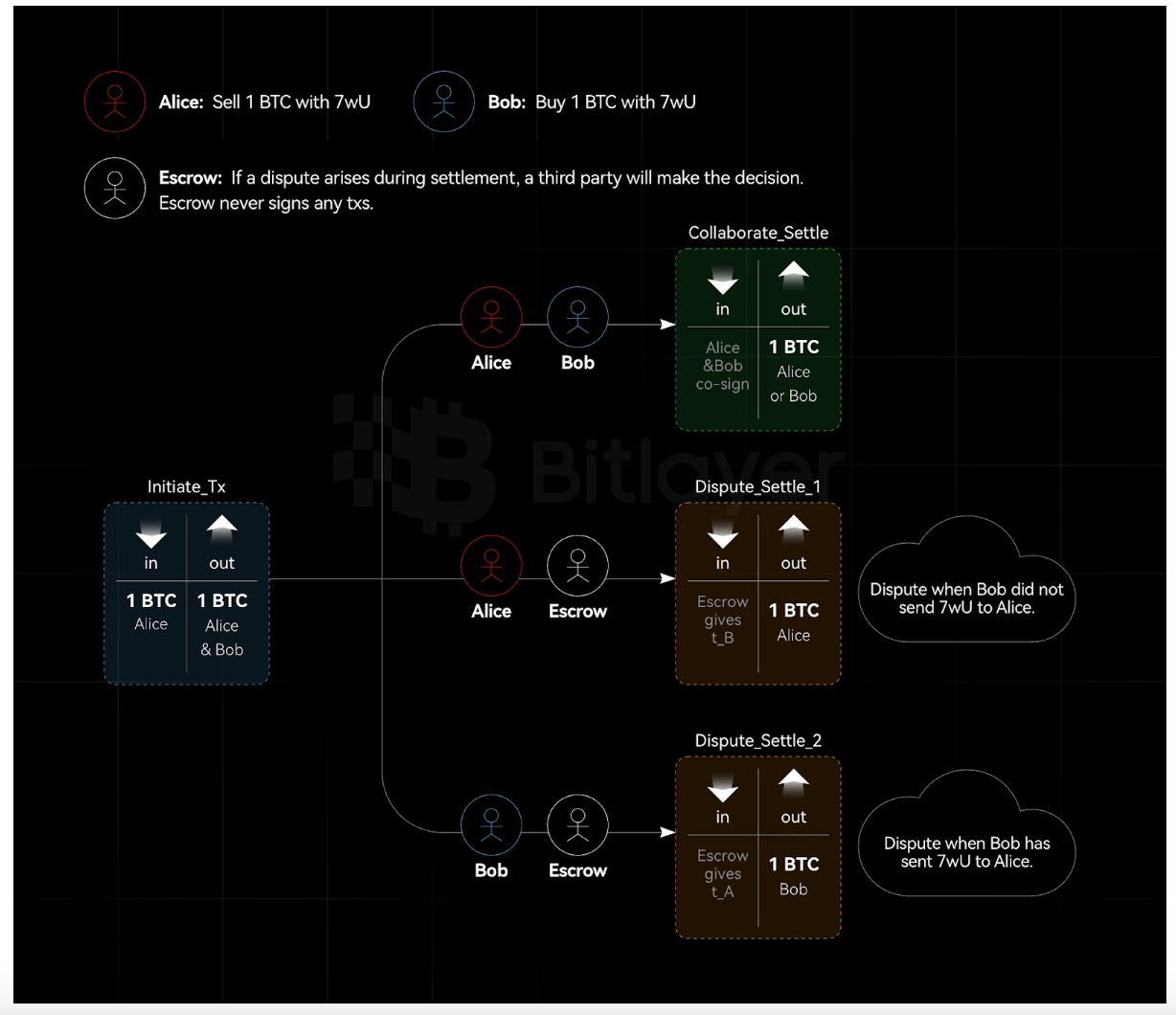
รูปที่ 3 การโฮสต์เนื้อหาแบบไม่โต้ตอบตามลายเซ็นของอะแดปเตอร์

ดังแสดงในรูปที่ 3 อลิซและบ็อบต้องการสร้างเอาท์พุตธุรกรรม 2 ใน 3 ด้วยกลยุทธ์ที่ซ่อนอยู่ซึ่งรวมถึงผู้ดูแลด้วย ขึ้นอยู่กับเงื่อนไข $c$ อลิซหรือบ็อบสามารถใช้เอาท์พุตธุรกรรมได้ หากมีข้อพิพาทระหว่าง Alice และ Bob ผู้ดูแล (คีย์สาธารณะ $E$, คีย์ส่วนตัว $e$) จะเป็นผู้ตัดสินใจว่า Alice หรือ Bob จะได้รับสินทรัพย์หรือไม่

• สร้างธุรกรรมการระดมทุนที่ไม่ได้ลงนามซึ่งส่ง BTC ไปยังเอาต์พุต MuSig 2 ใน 2 ระหว่าง Alice และ Bob

• Alice เลือกค่าสุ่ม $t_A$ และส่ง Schnorr pre-signature $(\hat{R__A,\hat{s__A)$ ของธุรกรรมที่มีอะแดปเตอร์เป็น $t_A ᐧ G$ ให้กับ Bob เอาต์พุตจะถูกส่งไปยัง Bob อลิซยังส่งข้อความไซเฟอร์ไปยัง Bob ซึ่งมี \textbf{verifiableการเข้ารหัส}$ ของความลับ $t_A$ และปรับคีย์สาธารณะเอสโครว์ $E$ เป็น $E_c = E + hash(E, c)G$ C = Enc (E_c, t_A)$. ในระหว่างกระบวนการนี้ หลังจากที่ Bob ได้รับลายเซ็นล่วงหน้าของ Alice แล้ว เขาก็เพิ่มลายเซ็นของตัวเอง ซึ่งไม่เป็นไปตาม 2 ใน 2 MuSig และดังนั้นจึงไม่สามารถใช้เงินทุนที่ได้ สามารถใช้เงินทุนได้เฉพาะในกรณีที่ Bob ทราบ $t_A$ (ซึ่งเอสโครว์เป็นผู้จัดหาให้) หรือหาก Alice ลงนามเพิ่มเติมในลายเซ็นฉบับเต็มและส่งให้กับ Bob

• ในทำนองเดียวกัน Bob ทำซ้ำขั้นตอน (2) โดยอิงตามความลับของอะแดปเตอร์ $t_B$ ในขณะนี้ ธุรกรรมที่ Bob ลงนามคือการส่งเงินทุนไปยัง Alice

• ทั้ง Alice และ Bob ตรวจสอบความถูกต้องของไซเฟอร์เท็กซ์ที่ได้รับ และยืนยันว่าไซเฟอร์เท็กซ์นั้นเป็นการเข้ารหัสความลับของ $E_c$ ดังนั้นจึงเป็นการลงนามและถ่ายทอดธุรกรรมการระดมทุน การเข้ารหัสที่ตรวจสอบได้ช่วยลดความจำเป็นในการให้ผู้ดูแลเข้าร่วมในขั้นตอนการตั้งค่า และไม่จำเป็นต้องมีสัญญาสาธารณะ $c$

• เมื่อมีข้อพิพาท Alice และ Bob สามารถส่งข้อความไซเฟอร์เท็กซ์และเงื่อนไข c ไปยังผู้ดูแลได้ และผู้ดูแลสามารถตัดสินสถานการณ์จริงและใช้คีย์ส่วนตัวที่ปรับแล้ว $e+hash(E, c)$ เพื่อถอดรหัสและส่ง $t_A /t_B $ ถึงบ๊อบ/อลิซ

หากไม่มีข้อโต้แย้ง Alice และ Bob สามารถใช้เอาต์พุต MuSig 2 ใน 2 ได้ตามต้องการ หากมีข้อพิพาท ฝ่ายใดฝ่ายหนึ่งสามารถติดต่อเอสโครว์และขอข้อมูลลับของอะแดปเตอร์ $t_A$ หรือ $t_B$ ดังนั้นฝ่ายใดฝ่ายหนึ่งสามารถกรอกลายเซ็นอะแดปเตอร์และเผยแพร่ธุรกรรมการชำระเงินได้โดยใช้ความช่วยเหลือจากฝ่ายเอสโครว์

4.2 การเข้ารหัสที่ตรวจสอบได้

รูปแบบการเข้ารหัสที่ตรวจสอบได้แบบคลาสสิกซึ่งอิงตามลอการิทึมแบบแยกส่วน ( Practical Verifiable Encryption and Decryption of Discrete Logarithms ) ไม่สามารถใช้ได้กับอะแดปเตอร์ Secp 256 k 1 เนื่องจากรองรับเฉพาะการตรวจสอบกลุ่มที่มีโครงสร้างพิเศษเท่านั้น

ปัจจุบัน มีวิธีที่น่าหวังสองวิธีในการเข้ารหัสที่ตรวจสอบได้โดยใช้ลอการิทึมแยก Secp 256 k 1 ได้แก่ Purify และ Juggling

เดิมที Purify ได้รับการเสนอให้สร้างโปรโตคอล MuSig ด้วย deterministic nonce (DN) ซึ่งกำหนดให้ผู้ลงนามแต่ละคนต้องใช้ความรู้เป็นศูนย์เพื่อพิสูจน์ว่า nonce ของพวกเขาเป็นผลมาจากการใช้ฟังก์ชัน pseudorandom (PRF) อย่างถูกต้องกับกุญแจสาธารณะและข้อความ Purify PRF ได้รับการนำไปใช้อย่างมีประสิทธิภาพในวงจรเลขคณิตของโปรโตคอลความรู้เป็นศูนย์ Bulletproofs สำหรับการสร้างแผนการเข้ารหัสที่ตรวจสอบได้บนลอการิทึมแยกเหนือ Secp 256 k 1 กล่าวอีกนัยหนึ่ง ให้ใช้ zkSnark สำหรับการเข้ารหัสที่ตรวจสอบได้

การเข้ารหัสการ เล่นกล ประกอบด้วยสี่ขั้นตอน: (1) แบ่งลอการิทึมแยก $x$ ออกเป็นหลาย ๆ ส่วน $x_k$ ที่มีความยาว $l$ โดยที่ $x = \sum _k 2 ^{(k-1)l} x_k$; ( 2) การเข้ารหัส ElGamal ของแฟรกเมนต์ $x_k ᐧ G$ โดยใช้คีย์สาธารณะ $Y$ $\{ D_k, E_k\} = \{ x_k ᐧ G + r_k ᐧ Y, r_k ᐧ G \}$ (3 ) สร้างการพิสูจน์ช่วง สำหรับแต่ละ $x_k ᐧ G$ โดยพิสูจน์ว่า $D_k$ เป็นความมุ่งมั่นของ Pedersen $x_k ᐧ G + r_k ᐧ Y$ และค่าของมันน้อยกว่า $ 2 ^l$; (4) ใช้โปรโตคอล sigma เพื่อพิสูจน์ว่า $ \{sum D_k, sum E_k\}$ เป็นการเข้ารหัสที่ถูกต้องของ $x_k ᐧ G$

ในกระบวนการถอดรหัส แต่ละ $x_k ᐧ G$ จะถูกถอดรหัสสำหรับ $\{D_k, E_k\}$ จากนั้น $x_k$ จะถูกค้นหาอย่างละเอียด (ช่วงค่าคือ $[ 0, 2 ^l)$)

การทำให้บริสุทธิ์จำเป็นต้องมีการดำเนินการ PRF ภายใน Bulletproofs ซึ่งค่อนข้างซับซ้อน ในขณะที่ Juggling นั้นง่ายกว่าในทางทฤษฎี นอกจากนี้ ความแตกต่างระหว่างขนาดการพิสูจน์ เวลาในการพิสูจน์ และเวลาการตรวจสอบยังมีน้อยมาก

5. สรุป

บทความนี้ให้คำอธิบายโดยละเอียดเกี่ยวกับหลักการของลายเซ็นอะแดปเตอร์ Schnorr/ECDSA และการแลกเปลี่ยนอะตอมมิกแบบข้ามสายโซ่ มีการวิเคราะห์เชิงลึกเกี่ยวกับปัญหาการรั่วไหลของตัวเลขสุ่มและการทำซ้ำในลายเซ็นของอแด็ปเตอร์ และเสนอให้ใช้ RFC 6979 เพื่อแก้ไขปัญหาเหล่านี้ นอกจากนี้ ในสถานการณ์สมมติแอปพลิเคชันแบบข้ามสายโซ่ มีการวิเคราะห์ในรายละเอียดว่าไม่เพียงแต่ควรพิจารณาความแตกต่างระหว่างโมเดล UTXO และรูปแบบบัญชีของบล็อกเชนเท่านั้น แต่ยังรวมถึงลายเซ็นของอะแดปเตอร์ที่สนับสนุนอัลกอริธึมที่แตกต่างกัน เส้นโค้งที่แตกต่างกัน และอื่นๆ ปัญหา. สุดท้ายนี้ ลายเซ็นของอแด็ปเตอร์จะถูกขยายและนำไปใช้เพื่อให้เกิดการดูแลสินทรัพย์ดิจิทัลแบบไม่โต้ตอบ และจะแนะนำการเข้ารหัสเบื้องต้นที่เกี่ยวข้อง - การเข้ารหัสที่ตรวจสอบได้ - จะถูกแนะนำโดยย่อ

การอ้างอิง

• Gugger J. Bitcoin-monero cross-chain atomic swap[J] Cryptology ePrint Archive, 2020.

• Fournier L. ลายเซ็นที่เข้ารหัสเพียงครั้งเดียวหรือที่เรียกว่าลายเซ็นอะแดปเตอร์[J] 2019, 2019

• https://crypto-in-action.github.io/ecdsa-blockchain-dangers/190816-secp256k1-ecdsa-dangers.pdf

• Pornin T. การใช้อัลกอริธึมลายเซ็นดิจิทัล (DSA) และอัลกอริธึมลายเซ็นดิจิทัลแบบวงรี (ECDSA) [R] 2013

• Komlo C, Goldberg I. FROST: ลายเซ็นเกณฑ์ Schnorr ที่ปรับให้เหมาะสมรอบแบบยืดหยุ่น [C]//พื้นที่ที่เลือกในการเข้ารหัส: การประชุมนานาชาติครั้งที่ 27, แฮลิแฟกซ์, โนวาสโกเทีย, แคนาดา (กิจกรรมเสมือนจริง), 21-23 ตุลาคม 2020, เอกสารที่เลือกแก้ไขฉบับปรับปรุง 27 . สำนักพิมพ์สปริงเกอร์อินเตอร์เนชั่นแนล, 2021: 34-65.

• https://github.com/BlockstreamResearch/scriptless-scripts/blob/master/md/NITE.md

• https://particl.news/the-dex-revolution-basicswap-and-private-ethereum-swaps/

• Camenisch J, Shoup V. การเข้ารหัสและการถอดรหัสลอการิทึมแบบไม่ต่อเนื่อง[C]//การประชุมวิทยาการเข้ารหัสลับนานาชาติประจำปี เบอร์ลิน, ไฮเดลเบิร์ก: Springer Berlin Heidelberg, 2003: 126-144

• Nick J, Ruffing T, Seurin Y และคณะ: Schnorr multi-signatures พร้อม nonces ที่ตรวจสอบได้[C]//การประชุม ACM SIGSAC Conference on Computer and Communications Security ปี 2020: 1717-1731

• Shlomovits O, Leiba O. Jugglingswap: การแลกเปลี่ยนข้ามสายโซ่แบบไร้สคริปต์ [J] arXiv พิมพ์ล่วงหน้า arXiv: 2007.14423, 2020