ชื่อต้นฉบับ: "สินค้าแห้ง | ลายเซ็นของ Schnorr สามารถปรับปรุง Bitcoin ได้อย่างไร" ผู้เขียน Stepan

ในขณะที่อ่านเอกสาร MuSig โดย Blockstream ฉันเอาแต่จินตนาการว่าสิ่งนี้มีความหมายต่อฉันอย่างไรในฐานะผู้ใช้ Bitcoin ฉันพบว่าคุณลักษณะบางอย่างของลายเซ็นของ Schnorr นั้นยอดเยี่ยมและสะดวกมาก และคุณลักษณะบางอย่างก็ค่อนข้างน่ารำคาญ ในบทความนี้ฉันหวังว่าจะแบ่งปันความคิดของฉันกับคุณ แต่ก่อนอื่น เรามาสรุปสั้นๆ ก่อน

อัลกอริทึมลายเซ็นโค้งวงรี

ระบบการเป็นเจ้าของ Bitcoin ปัจจุบันใช้ ECDSA (Elliptic Curve Signature Algorithm) เมื่อเซ็นข้อความ m เราจะแฮชข้อความก่อนเพื่อให้ได้ค่าแฮช เช่น z = hash(m) เราต้องการหมายเลขสุ่ม (หรืออย่างน้อยก็ดูเหมือนสุ่ม) k ในที่นี้ เราไม่ต้องการเชื่อถือตัวสร้างตัวเลขสุ่ม (มีข้อผิดพลาดและข้อบกพร่องที่เกี่ยวข้องกับตัวสร้างตัวเลขสุ่มต่ำกว่ามาตรฐานมากเกินไป) ดังนั้นโดยทั่วไปเราจะใช้ RFC6979 ตามค่าลับที่เราทราบ และเราต้องการลงชื่อข้อความ คำนวณ กำหนด k.

การใช้คีย์ส่วนตัว pk เราสามารถสร้างลายเซ็นสำหรับข้อความ m ซึ่งประกอบด้วยตัวเลขสองตัว: r (พิกัด x ของจุดสุ่ม R = k * G) และ s = (z + r*pk)/k

คำอธิบายภาพ

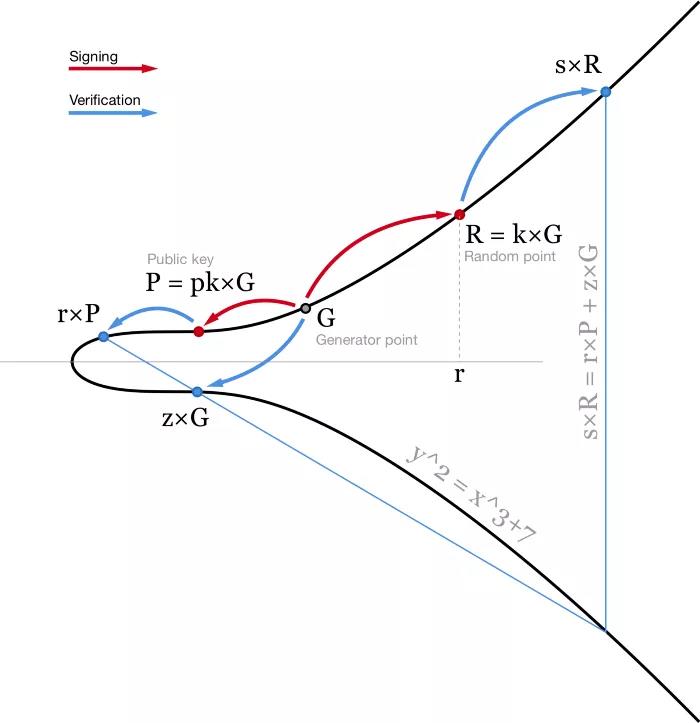
- ไดอะแกรมอัลกอริทึม ECDSA เพื่อจุดประสงค์ในการอธิบาย เส้นโค้งวงรีทำงานบนฟิลด์ของจำนวนจริง −

อัลกอริทึมนี้ใช้กันทั่วไปและใช้งานง่ายมาก แต่ยังมีช่องว่างสำหรับการปรับปรุง ประการแรก การตรวจสอบลายเซ็นเกี่ยวข้องกับการหาร (1/s) และการคูณสองจุด และการดำเนินการเหล่านี้ต้องใช้การคำนวณอย่างมาก ในเครือข่าย Bitcoin ทุกโหนดต้องตรวจสอบทุกธุรกรรม ดังนั้นเมื่อคุณส่งธุรกรรมในเครือข่าย โหนดนับพันในเครือข่ายทั้งหมดต้องตรวจสอบลายเซ็นของคุณ ดังนั้นแม้ว่าขั้นตอนการเซ็นชื่อจะมีราคาแพงขึ้น แต่ก็ยังมีประโยชน์มากในการทำให้การตรวจสอบลายเซ็นง่ายขึ้น

ลายเซ็น Schnorr

ลายเซ็น Schnorr

คำอธิบายภาพ

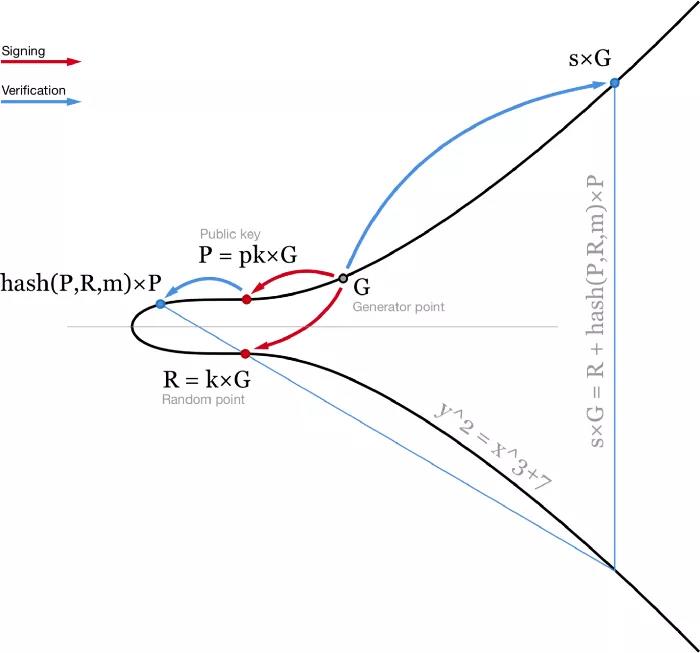
- ลายเซ็น Schnorr แบบกราฟิกและการตรวจสอบ -

สมการนี้เป็นเชิงเส้น ดังนั้นสมการหลายสมการจึงสามารถเพิ่มและลบได้ในขณะที่เครื่องหมายความเท่าเทียมกันยังคงอยู่ สิ่งนี้นำเราไปสู่คุณสมบัติที่ดีหลายประการของลายเซ็น Schnorr

1. การตรวจสอบเป็นชุด

เมื่อตรวจสอบความถูกต้องของบล็อกบนบล็อกเชน เราจำเป็นต้องตรวจสอบว่าลายเซ็นของธุรกรรมทั้งหมดในบล็อกนั้นถูกต้อง หากหนึ่งในนั้นไม่ถูกต้อง ไม่สำคัญว่าอันไหน - เราต้องปฏิเสธบล็อกทั้งหมด

แต่ละลายเซ็นของ ECDSA จะต้องได้รับการตรวจสอบโดยเฉพาะ หมายความว่าหากบล็อกหนึ่งมีลายเซ็น 1,000 รายการ เราจำเป็นต้องคำนวณการหาร 1,000 และการคูณ 2,000 จุด รวมเป็นการดำเนินการหนักประมาณ 3,000 ครั้ง

แต่ด้วยลายเซ็น Schnorr เราสามารถรวมสมการการตรวจสอบลายเซ็นทั้งหมดและบันทึกการคำนวณบางส่วนได้ ในบล็อกธุรกรรม 1,000 รายการ เราสามารถตรวจสอบได้:

(s1+s2+…+s1000) × G=(R1+…+R1000)+(hash(P1,R1,m1)×P1+ hash(P2,R2,m2)×P2+…+hash(P1000,R1000,m1000)×P1000)

คำอธิบายภาพ

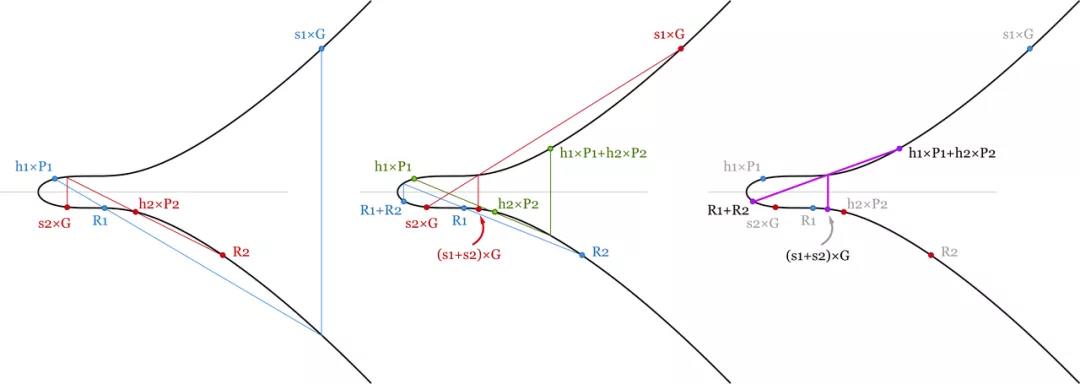
- การตรวจสอบแบทช์ของสองลายเซ็น เนื่องจากสมการการตรวจสอบเป็นแบบบวกเชิงเส้น ตราบใดที่ลายเซ็นทั้งหมดถูกต้อง ผลรวมของสมการเหล่านี้จะต้องถูกสร้างขึ้นด้วย เราประหยัดการคำนวณบางอย่างเนื่องจากการบวกสเกลาร์และจุดนั้นง่ายกว่าการคูณจุดมาก -

2. การสร้างคีย์

เราต้องการรักษาบิตคอยน์ของเราให้ปลอดภัย ดังนั้นเราอาจต้องการควบคุมมันด้วยคีย์ส่วนตัวที่แตกต่างกันอย่างน้อยสองคีย์ หนึ่งใช้กับแล็ปท็อปหรือโทรศัพท์มือถือ (กระเป๋าเงินออนไลน์, กระเป๋าสตางค์ร้อน) และอีกใบเก็บไว้ในกระเป๋าสตางค์ฮาร์ดแวร์/กระเป๋าสตางค์เย็น แม้ว่าหนึ่งในนั้นจะรั่วไหล เรายังคงควบคุมบิตคอยน์ของเรา

ปัจจุบัน วิธีการใช้กระเป๋าเงินดังกล่าวคือการใช้สคริปต์หลายลายเซ็นแบบ 2-2 นั่นคือ การทำธุรกรรมต้องมีสองลายเซ็นอิสระ

ด้วยลายเซ็น Schnorr เราสามารถใช้คีย์คู่หนึ่ง (pk1,pk2) และสร้างลายเซ็นร่วมกันโดยใช้คีย์สาธารณะที่ใช้ร่วมกัน P = P1 + P2 = pk1 * G + pk2 * G เมื่อสร้างลายเซ็น เราจำเป็นต้องสร้างตัวเลขสุ่ม (k1, k2) บนอุปกรณ์ทั้งสอง และสร้างจุดสุ่มสองจุด Ri = ki * G และเพิ่มแฮช (P, R1 + R2, m ) คุณจะได้รับ s1 และ s2 (เพราะ si = ki + hash(P, R, m)* pki ) สุดท้าย เพิ่มทั้งหมดเพื่อให้ได้ลายเซ็น (R, s) = (R1+R2, s1+s2) ซึ่งเป็นลายเซ็นที่ใช้ร่วมกันของเรา ซึ่งสามารถตรวจสอบได้ด้วยคีย์สาธารณะที่ใช้ร่วมกัน ไม่มีใครสามารถบอกได้ว่าเป็นลายเซ็นรวมหรือไม่ ดูเหมือนว่าลายเซ็นของ Schnorr ทั่วไป

อย่างไรก็ตาม มีปัญหาสามประการเกี่ยวกับแนวทางนี้

ปัญหาแรกอยู่ที่ UI ในการเริ่มต้นธุรกรรม เราจำเป็นต้องเริ่มต้นการโต้ตอบหลายรอบบนอุปกรณ์สองเครื่อง - สำหรับการคำนวณค่า R ทั่วไป และสำหรับการเซ็นชื่อ ในกรณีของคีย์ส่วนตัวสองคีย์ เราต้องไปที่กระเป๋าเงินเย็นเพียงครั้งเดียว: เราสามารถเตรียมธุรกรรมเพื่อลงนามในกระเป๋าเงินร้อน เลือก k1 และสร้าง R1 = k1 * G จากนั้นใส่ธุรกรรมที่จะลงนามพร้อมกัน ด้วยข้อมูลเหล่านี้ผ่านในกระเป๋าเงินเย็นและลงนาม เนื่องจากมี R1 อยู่แล้ว การทำธุรกรรมลายเซ็นจึงสามารถทำได้เพียงรอบเดียวในกระเป๋าเงินเย็น จากกระเป๋าเงินเย็นเราได้รับ R2 และ s2 และส่งกลับไปที่กระเป๋าเงินร้อน กระเป๋าเงินร้อนใช้ธุรกรรมลายเซ็น (k1, R1) ที่กล่าวมาข้างต้น และผลรวมของลายเซ็นทั้งสองสามารถเผยแพร่ธุรกรรมไปยังโลกภายนอกได้

ประสบการณ์นี้ไม่ต่างจากที่เราทำได้ในตอนนี้ และทุกครั้งที่คุณเพิ่มรหัสส่วนตัวเพิ่มเติม ปัญหาก็จะยิ่งซับซ้อนมากขึ้น สมมติว่าคุณมีความมั่งคั่งที่ควบคุมร่วมกันโดยคีย์ส่วนตัว 10 อัน และคีย์ส่วนตัว 10 อันถูกเก็บไว้ในส่วนต่าง ๆ ของโลก การส่งธุรกรรมในเวลานี้เป็นเรื่องยากสำหรับคุณ! ในอัลกอริทึม ECDSA ปัจจุบัน คุณต้องไปที่อุปกรณ์แต่ละเครื่องเพียงครั้งเดียว แต่ถ้าคุณใช้การรวมคีย์ของ Schnorr คุณต้องไปที่สองครั้งเพื่อรับ Ri และลงชื่อทั้งหมด ในกรณีนี้ แทนที่จะใช้การรวม การเซ็นชื่อด้วยคีย์ส่วนตัวทีละรายการอาจดีกว่า - เพื่อให้ต้องมีการโต้ตอบเพียงรอบเดียว

หลังจากบทความจบลง ฉันได้รับคำติชมจาก Manu Drijvers: ในรูปแบบหลายลายเซ็นที่ปลอดภัยซึ่งพิสูจน์ได้ คุณต้องโต้ตอบ 3 รอบ:

• เลือกตัวเลขสุ่ม ki และจุดสุ่มที่สอดคล้องกัน Ri = ki \G จากนั้นบอกค่าแฮชของ Ri ของอุปกรณ์แต่ละเครื่อง ti=hash(Ri) จากนั้นอุปกรณ์แต่ละเครื่องจะมั่นใจได้ว่าคุณไม่ทราบความคิดในการเปลี่ยนตัวเลขสุ่มของผู้อื่น*

• เข้าสู่ระบบ

• เข้าสู่ระบบ

ปัญหาที่สองคือการโจมตีคีย์ Rogue ที่รู้จัก กระดาษอธิบายได้ดีมากดังนั้นฉันจะไม่ลงรายละเอียด อาจหมายความว่าหากอุปกรณ์เครื่องใดเครื่องหนึ่งของคุณถูกแฮ็ก (เช่น hot wallet ของคุณถูกแย่งชิง) และแสร้งทำเป็นว่ารหัสสาธารณะของคุณคือ (P1 - P2) คุณสามารถควบคุมรหัสส่วนตัวที่ใช้ร่วมกันของคีย์ส่วนตัวทั้งสองได้เฉพาะกับรหัสส่วนตัวเท่านั้น คีย์ pk1 กองทุน วิธีแก้ปัญหาง่ายๆ คือต้องใช้รหัสส่วนตัวเพื่อลงนามรหัสสาธารณะที่เกี่ยวข้องเมื่อตั้งค่าอุปกรณ์

มีปัญหาสำคัญประการที่สาม คุณไม่สามารถลงชื่อด้วย deterministic k หากคุณใช้ deterministic k แฮ็กเกอร์สามารถรับรหัสส่วนตัวของคุณด้วยการโจมตีง่ายๆ เพียงครั้งเดียว นี่คือการโจมตี: แฮ็กเกอร์บางคนเจาะเข้าไปในแล็ปท็อปของคุณและเข้าควบคุมหนึ่งในคีย์ส่วนตัวทั้งหมด (เช่น pk1) เรารู้สึกว่าเงินยังคงปลอดภัย เนื่องจากการใช้ bitcoin ของเราต้องมีลายเซ็นรวมของ pk1 และ pk2 ดังนั้นเราจึงเริ่มต้นธุรกรรมตามปกติ เตรียมธุรกรรมที่จะลงนามและ R1 ส่งไปยังกระเป๋าเงินฮาร์ดแวร์ของเรา และหลังจากที่กระเป๋าเงินฮาร์ดแวร์ลงนาม ส่ง (R2, s2) กลับไปที่กระเป๋าเงินร้อน... wallet เกิดข้อผิดพลาด ไม่สามารถลงนามและออกอากาศให้เสร็จสมบูรณ์ได้ เราจึงลองอีกครั้ง แต่คราวนี้คอมพิวเตอร์ที่ถูกแฮ็กใช้ตัวเลขสุ่มอื่น - R1' เราลงนามธุรกรรมเดียวกันในกระเป๋าเงินฮาร์ดแวร์ของเรา และส่ง (R2, s2') กลับไปยังคอมพิวเตอร์ที่ถูกแฮ็ก ครั้งนี้ไม่มีอีกแล้ว - bitcoins ของเราหมดแล้ว

ในการโจมตีนี้ แฮ็กเกอร์ได้รับลายเซ็นที่ถูกต้องสองรายการของธุรกรรมเดียวกัน: (R1, s1, R2, s2) และ (R1', s1', R2, s2') R2 นี้เหมือนกัน แต่ R = R1 + R2 และ R' = R1' + R2 ต่างกัน ซึ่งหมายความว่าแฮ็กเกอร์สามารถคำนวณคีย์ส่วนตัวที่สองของเรา: s2-s2'=(hash(P,R1+R2,m)-hash(P,R1'+R2,m))⋅pk2 หรือ pk2 =(s2-s2 ')/(แฮช(P,R1+R2,m)-แฮช(P,R1'+R2,m)). ฉันพบว่าสิ่งนี้เป็นส่วนที่ไม่สะดวกที่สุดในการรวมคีย์ - เราต้องใช้ตัวสร้างตัวเลขสุ่มที่ดีทุกครั้งเพื่อรวมอย่างปลอดภัย

3. Musig

MuSig แก้ไขปัญหาอย่างหนึ่ง - การโจมตีด้วยคีย์อันธพาลจะไม่ทำงานอีกต่อไป เป้าหมายในที่นี้คือการรวมลายเซ็นและคีย์สาธารณะจากหลายฝ่าย/การตั้งค่าหลายรายการ โดยที่คุณไม่ต้องพิสูจน์ว่าคุณมีคีย์ส่วนตัวที่สอดคล้องกับคีย์สาธารณะเหล่านั้น

ลายเซ็นรวมสอดคล้องกับคีย์สาธารณะรวม แต่ใน MuSig แทนที่จะรวมพับลิกคีย์ของผู้ลงนามร่วมทั้งหมดโดยตรง เราจะคูณด้วยพารามิเตอร์บางตัว เพื่อให้พับลิกคีย์รวม P = hash(L,P1)×P1 + ... + hash(L,Pn ) × พน. ที่นี่ L = hash(P1,...,Pn) - หมายเลขสาธารณะนี้ขึ้นอยู่กับคีย์สาธารณะทั้งหมด คุณสมบัติไม่เชิงเส้นของ L ป้องกันผู้โจมตีจากการสร้างรหัสสาธารณะพิเศษเพื่อเริ่มการโจมตี แม้ว่าผู้โจมตีจะรู้ว่าแฮช(L,Patk)×Patk ของเขาควรเป็นอย่างไร แต่เขาก็ไม่สามารถอนุมาน Patk จากมันได้—เช่นเดียวกับที่คุณต้องการอนุมานคีย์ส่วนตัวจากคีย์สาธารณะ

กระบวนการอื่นๆ ของการสร้างลายเซ็นนั้นคล้ายคลึงกันมากกับที่อธิบายไว้ข้างต้น เมื่อสร้างลายเซ็น ผู้ลงนามร่วมแต่ละคนจะเลือกหมายเลขสุ่ม ki และแบ่งปัน Ri = ki * G กับผู้อื่น จากนั้นพวกเขารวมคะแนนสุ่มทั้งหมดเพื่อรับ R=R1+…+Rn แล้วสร้างลายเซ็น si = ki + hash(P,R,m) ⋅ hash(L,Pi) ⋅ pki ดังนั้น ลายเซ็นรวมคือ (R, s)=(R1+…+Rn, s1+…+sn) และวิธีตรวจสอบลายเซ็นก็เหมือนเดิม: s×G = R + hash(P,R,m )×ป.

4. Merkle tree หลายลายเซ็น

นอกจากนี้ คุณอาจสังเกตเห็นว่า MuSig และการรวมคีย์กำหนดให้ *ผู้ลงนามทุกคนลงนามในธุรกรรม* แต่ถ้าคุณต้องการทำสคริปต์แบบหลายลายเซ็น 2-3 รายการล่ะ เราสามารถใช้การรวมลายเซ็น ณ จุดนี้ได้ไหม หรือเราต้องใช้ OP_CHECKMULTISIG ตามปกติและเซ็นแยกกัน (หมายเหตุผู้แปล: OP_CHECKMULTISIG เป็นรหัสการดำเนินการสำหรับ Bitcoin เพื่อตรวจสอบสคริปต์หลายลายเซ็นโค้งวงรี)

ให้ฉันเริ่มต้นด้วยคำตอบ ใช่ แต่ข้อตกลงจะแตกต่างกันเล็กน้อย เราสามารถพัฒนา opcode ที่คล้ายกับ OP_CHECKMULTISIG ได้ ยกเว้นว่าจะตรวจสอบว่าลายเซ็นรวมสอดคล้องกับองค์ประกอบบนแผนผัง Merkle ของคีย์สาธารณะหรือไม่

ตัวอย่างเช่น หากเราต้องการใช้คีย์สาธารณะ P1, P2 และ P3 เพื่อสร้างสคริปต์หลายลายเซ็น 2-3 รายการ เราจำเป็นต้องใช้คีย์สาธารณะเหล่านี้ทั้งหมด (P1, P2), (P2, P3), (P1 , P3) เพื่อสร้าง Merkle tree และเผยแพร่รากของ Merkle tree ในสคริปต์การล็อก

ข้อความ

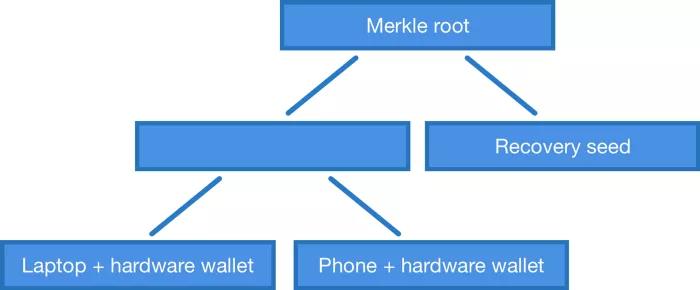
แต่ด้วยแผนผังคีย์สาธารณะของ Merkle เราไม่จำเป็นต้องจำกัดสคริปต์หลายลายเซ็น เราสามารถสร้างต้นไม้โดยใช้คีย์สาธารณะร่วมกัน ตัวอย่างเช่น หากเรามีแล็ปท็อป โทรศัพท์ กระเป๋าเงินฮาร์ดแวร์ และตัวช่วยจำ เราสามารถสร้าง Merkle tree ที่ช่วยให้เราใช้แล็ปท็อป + กระเป๋าเงินฮาร์ดแวร์ โทรศัพท์ + กระเป๋าเงินฮาร์ดแวร์ หรือจำคำแยกต่างหากเพื่อใช้ Bitcoin . นี่คือสิ่งที่ OP_CHECKMULTISIG ปัจจุบันไม่สามารถทำได้ เว้นแต่คุณจะใช้การควบคุมโฟลว์สไตล์ "IF - Else" เพื่อสร้างสคริปต์ที่ซับซ้อนมากขึ้น

สรุปแล้ว

ลายเซ็นของ Schnorr นั้นยอดเยี่ยม พวกเขาช่วยแก้ปัญหาค่าใช้จ่ายในการคำนวณบางอย่างในการตรวจสอบบล็อก และยังทำให้เรารวบรวมคีย์ได้อีกด้วย แบบหลังค่อนข้างไม่สะดวกในการใช้งาน แต่เราไม่ได้บังคับให้คนอื่นใช้ - เรายังสามารถใช้แบบแผนหลายลายเซ็นปกติได้อยู่ดี โดยใช้ลายเซ็นเดี่ยวแบบไม่รวม

ฉันแทบรอไม่ไหวที่จะใช้ลายเซ็น Schnorr หวังว่าโปรโตคอล Bitcoin จะรวมเข้าด้วยกันในไม่ช้า

(เกิน)

(เกิน)