この記事の著者: p0n1@安比实验
libsnark は現在、zk-SNARKs 回路を実装するための最も重要なフレームワークであり、多くのプライベート トランザクションやプライバシー コンピューティング関連のプロジェクトで広く使用されており、その中で Zcash が最も有名です。 Zcash は、Sapling バージョンがアップグレードされるまで、libsnark を使用して回路を実装していました (後に bellman に置き換えられました)。 libsnark は、zk-SNARKs テクノロジーの最初の大規模アプリケーションをサポートおよび促進し、最新の理論とゼロ知識証明テクノロジーの工学的実装の間のギャップを埋めていると言っても過言ではありません。
この一連の記事を通じて、すべての開発者が短期間で libsnark を使い始め、libsnark の基本概念を段階的に理解し、zk-SNARKs 回路の開発方法を学び、証明の生成と検証を完了できることを願っています。そして最後にゼロ知識証明を実際のビジネスに適用します。
1. zk-SNARKs と libsnark の背景の紹介
ゼロ知識証明は、現時点で最も有望で想像力に富んだ暗号ブラックテクノロジーかもしれません。そして、zk-SNARKsとはゼロ知識証明スキームの一種の略称で、正式名称はZero-Knowledge Succinct Non-interactive Arguments of Knowledgeです。この名前には、そのほぼすべての技術的特徴が含まれています。つまり、命題の正しさは、他の情報を明らかにすることなく証明でき、最終的に生成される証明は簡潔 (Succinct) です。これは、最終的に生成される証明が十分に小さいことを意味します。計算量とは関係なく、定数です。平たく言えば、理論的には、プライバシーを一切公開することなく他の人に何かを証明することができ、内容を証明するために必要な計算量に関係なく、生成される証明のサイズは小さく、検証コストは非常に低くなります。あまりにもうますぎる話ですね。
zk-SNARK は、プライバシー保護、ブロックチェーンの拡張、検証可能なコンピューティングなど、多くのシナリオに適用できます。この記事では、zk-SNARKS とゼロ知識証明の理論的な詳細については紹介しません。詳しくない学生やさらに詳しく知りたい学生は、他の記事や論文を読んでください。
Vitalik の zk-SNARK に関する有名な 3 つのブログ投稿などです。
https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627
https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6
または、Xiang Cheng @HUST が書いたものを読んでください「ゼロ知識証明の Zk-SNARK を簡単に言うと」と東澤は書いた。「ゼロ知識証明についての話 II: 短い無対話証明 (SNARK)」。
もちろんAmbi Labにも注目してくださいそしてそして「ゼロから学ぶzk-SNARK」シリーズ、および Ambi Labs からのメンテナンス「ゼロ知識証明学習リソースの概要」詳細については、を参照してください。
この記事の主人公である libsnark は、SCIPR Lab によって開発および保守されている、zk-SNARKs アプリケーションを開発するための C++ コード ライブラリです。 libsnark エンジニアリングの実装の背後にある理論的基礎は、近年 (特に 2013 年以降) のゼロ知識証明、特に zk-SNARK の方向における一連の重要な論文です。最も有名なもののいくつかは次のとおりです。
[GGPR13] Quadratic span programs and succinct NIZKs without PCPs , Rosario Gennaro, Craig Gentry, Bryan Parno, Mariana Raykova, EUROCRYPT 2013
[PGHR13] Pinocchio: Nearly Practical Verifiable Computation , Bryan Parno, Craig Gentry, Jon Howell, Mariana Raykova, IEEE Symposium on Security and Privacy (Oakland) 2013
[BCGTV13] SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge , Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin, Eran Tromer, Madars Virza, CRYPTO 2013
[BCIOP13] Succinct non-interactive arguments via linear interactive Proofs , Nir Bitansky, Alessandro Chiesa, Yuval Ishai, Rafail Ostrovsky, Omer Paneth, Theory of Cryptography Conference 2013
[BCTV14a] Succinct non-interactive zero knowledge for a von Neumann architecture , Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza, USENIX Security 2014
[BCTV14b] Scalable succinct non-interactive arguments via cycles of elliptic curves , Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza, CRYPTO 2014
[Groth16] On the Size of Pairing-based Non-interactive Arguments , Jens Groth, EUROCRYPT 2016
libsnark の開発者は、上記の論文の多くの共著者である Eran Tromer など、この分野のトップの学者や研究専門家でもあります。
強固な理論的基盤とエンジニアリング能力により、libsnark の作成者は複雑さを単純化し、下図に示す高度な理論と複雑な式を 1 つずつ実現し、開発者の利便性を考慮して高度なエンジニアリングで簡潔なインターフェイスを抽象化することができます。並外れた理論研究を大規模な応用に拡張した先駆者たちに敬意を表します。

次の図は、MIT の libsnark コード寄稿の最初の作成者である Madars Virza から抜粋した libsnark のモジュール概要です。博士論文。
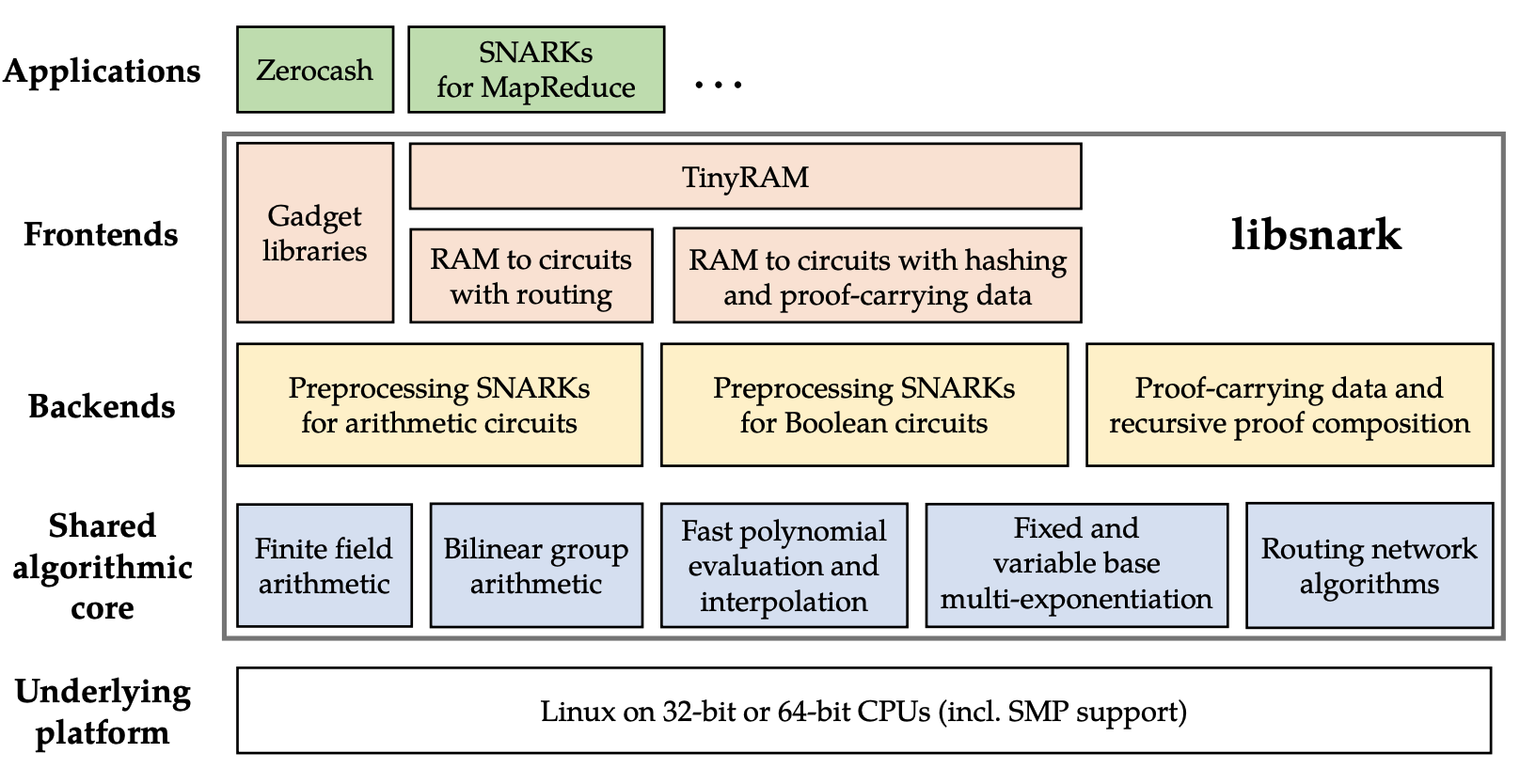
)
libsnark フレームワークは、複数の一般的な証明システムの実装を提供します。その中で、BCTV14a と Groth16 がよく使用されます。
で:
で:
zk_proof_systems/ppzksnark/r1cs_ppzksnark は BCTV14a に対応します
zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark は Groth16 に対応します
これら 2 つのプロトコルの実装の詳細を調べたい場合は、これら 2 つのディレクトリから直接開始できます。 ppzksnark は、zkSNARK の前処理を指します。ここでの pp/前処理とは、実際には、私たちがよく言う信頼できるセットアップのことを指します。つまり、証明が生成され検証される前に、生成アルゴリズムを通じて関連する公開パラメーター (証明キーと検証キー) を作成する必要があります。この事前生成されたパラメータを「共通参照文字列」(共通参照文字列)、または単に「共通参照文字列」とも呼びます。CRS。
2. 基本原則と手順
libsnark ライブラリを使用して zk-SNARKs アプリケーションを開発する手順は、原則として次の 4 つの手順に簡単に要約できます。
証明すべき命題をR1CS(Rank One Constraint System)として表現する
生成アルゴリズムを使用して、この命題の公開パラメーターを生成します (G)
証明アルゴリズムを使用して R1CS 充足可能性の証明を生成する (P)
検証アルゴリズム (V) を使用して証明を検証する
この記事この記事。
C(x, out) という関数があり、秘密 x が x^3 + x + 5 == out を満たすかどうかを判定し、満たす場合は true を返します。
function C(x, out) {
return ( x^3 + x + 5 == out );
}
最初のステップでは、関数 C(x, out) を libsnark で表現する必要があります。ここでは割愛しますので、詳しい処理は後ほど紹介します。
2 番目のステップは、次のジェネレーター関数 (G) に対応し、ラムダがランダムに生成されます。これは、信頼できるセットアップ プロセス中に生成されることがよくあります。"toxic waste"。人々はそれを「有毒廃棄物」と呼びたがります。なぜなら、それは適切に処分しなければならない(例えば、破棄しなければならず、誰もそれについて知ることができない)、そうしないと証明プロトコルのセキュリティに影響を与えるからです。
lambda <- random()
(pk, vk) = G(C, lambda)
最後に、証明鍵 (pk) と検証鍵 (vk) が生成されます。
3 番目のステップは、Prove 関数 (P) を使用して証明を生成することに対応します。ここで証明したいのは、証明者は秘密の値 x を知っており、その計算結果が方程式を満たすことができるということです。したがって、x、out、および pk を入力として P に渡し、最終的に証明を生成します。
proof = P(pk, out, x)
4 番目のステップは、Verify 関数 (V) を使用して証明を検証し、証明を渡し、out と vk を G に渡し、秘密を明かさずに方程式を満たす秘密の値が存在することを証明することです。
V(vk, out, proof) ?= true
開発者の主な作業負荷は、libsnark のインターフェイス規則に従って手動で命題を記述する C++ 回路コードを記述し、そのコードから R1CS 制約を構築する必要がある最初のステップに集中します。全体の処理は下図の演算→演算回路→R1CSにも相当します。

3. zk-SNARKsアプリケーション開発環境の構築
ハンズオン リンクに入り、すぐに libsnark を開始して、例を実行してみましょう。
まず、この記事に対応する libsnark の最小利用可能なサンプル コード ライブラリ libsnark_abc をダウンロードします。
git clone https://github.com/sec-bit/libsnark_abc.git
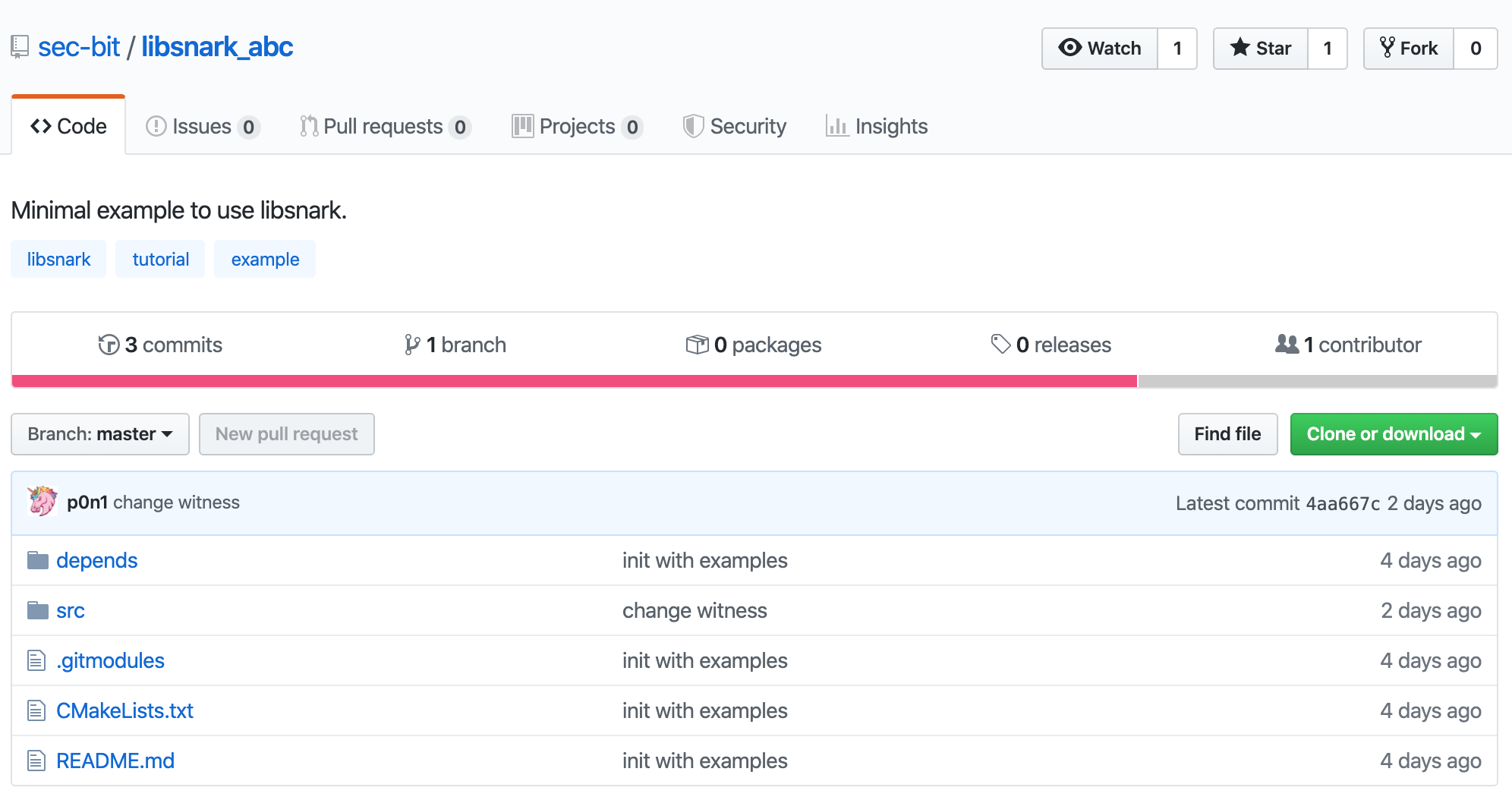
git サブモジュール経由で libsnark コードをプルします。
cd libsnark_abc
git submodule update --init --recursive
参照ライブラリプロジェクトのドキュメント関連する依存関係のインストールを完了します。 Ubuntu 16.04 LTS を例に挙げると、次のコンポーネントをインストールする必要があります。
sudo apt-get install build-essential cmake git libgmp3-dev libprocps4-dev python-markdown libboost-all-dev libssl-dev
ビルドフォルダーを初期化します。
mkdir build && cd build && cmake ..
この手順では macOS システムで問題が発生する可能性があります。を参照してください。この問題対処する。または、次のコマンドを使用してみてください。
mkdir build && cd build && CPPFLAGS=-I/usr/local/opt/openssl/include LDFLAGS=-L/usr/local/opt/openssl/lib PKG_CONFIG_PATH=/usr/local/opt/openssl/lib/pkgconfig cmake -DWITH_PROCPS=OFF -DWITH_SUPERCOP=OFF ..
成功した後も、ビルド ディレクトリでコンパイルされます。
make
コンパイルが成功すると、build/src ディレクトリに 3 つのバイナリ ファイルが表示されます。
main
range
test
この時点で、サンプル プロジェクトのコンパイルが完了しました。サンプルコードを実行してみてください。
./src/main
最後に、次のログが表示され、すべてが正常であることが示されます。 zkSNARK アプリケーション開発環境を正常に所有し、最初の zk-SNARK デモを正常に実行しました。
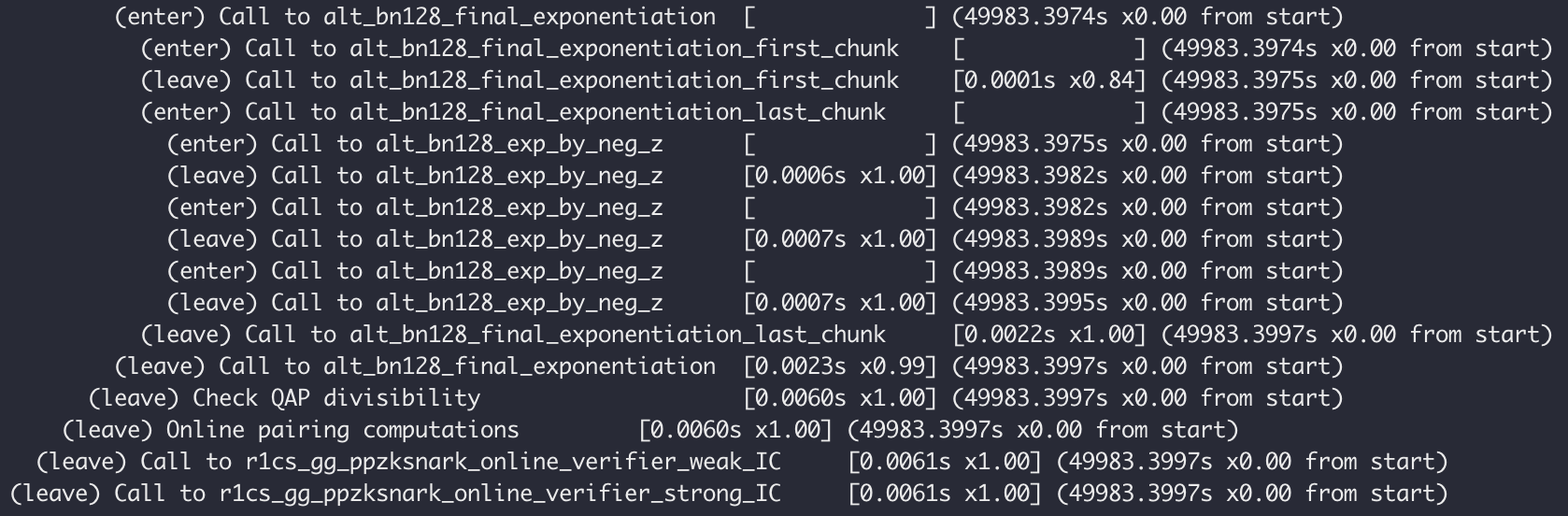
4. サンプルコードを理解する
一緒にコードを詳しく見てみましょう。サンプル プロジェクトには 3 つのコードが含まれています (記事の最後の付録も参照)。
まず src/main.cpp を見てみましょう。この例は Howard Wu の記事から引用しています。libsnark_tutorial、彼は libsnark の作者の 1 人でもあります。この記事の libsnark_abc のプロジェクト構造は彼の libsnark_tutorial に従って構築されており、「公式推奨スタイル」に属しますので、安心して食べてください😆。
コードは数十行しかありませんが、そのうちの run_r1cs_gg_ppzksnark() が主要部分です。実際に動作する実質的なコードは次の 5 行だけであることが簡単にわかります。
r1cs_gg_ppzksnark_keypair
r1cs_gg_ppzksnark_processed_verification_key
r1cs_gg_ppzksnark_proof
const bool ans = r1cs_gg_ppzksnark_verifier_strong_IC
const bool ans2 = r1cs_gg_ppzksnark_online_verifier_strong_IC
「長い」関数名だけから各ステップが何をしているのかはわかりますが、回路の構築方法の詳細はわかりません。実際、ここでは組み込みの r1cs_example を呼び出しているだけで、実装の詳細は隠されています。
そこで、より直観的な例を通して回路の詳細を学びましょう。 src/test.cpp を調べてください。この例は、Christian Lundkvist の資料を基にしています。libsnark-tutorial。
コードの先頭で参照されるヘッダー ファイルは次の 3 つだけです。
#include
#include
#include
前述したように、r1cs_gg_ppzksnark は Groth16 スキームに対応します。ここで gg が追加されるのは、r1cs_ppzksnark (つまり、BCTV14a スキーム) を区別するためです。これは、Generic Group Model (一般的なグループ モデル) を意味します。 Groth16 のセキュリティ証明は、より優れたパフォーマンスと短い証明を得るために、より強力なセキュリティ前提を引き換えるジェネリック グループ モデルに依存しています。
最初のヘッダー ファイルは、default_r1cs_gg_ppzksnark_pp タイプを導入するもので、2 つ目は証明に関連するさまざまなインターフェイスを導入するものです。 pb_variable は、回路関連の変数を定義するために使用されます。
次に、使用する有限フィールドを定義し、曲線パラメータを初期化するために、何らかの初期化が必要です。これはあらゆる準備に相当します。
typedef libff::Fr
default_r1cs_gg_ppzksnark_pp::init_public_params();
次に「証明すべき命題」とは何かを明確にする必要がある。ここで、前の例を使用して、秘密 x が方程式 x^3 + x + 5 == out を満たすことを証明することもできます。これは実際には Vitalik のブログ投稿です"Quadratic Arithmetic Programs: from Zero to Hero"で使用される例。以下の変更について初めて知る場合は、このブログ投稿を読んでみてください。
中間変数 sym_1、y、sym_2 を導入することにより、x^3 + x + 5 = out はいくつかの 2 次方程式に平坦化され、単純な乗算または加算のみを含むいくつかの式が算術回路の乗算ゲートと加算に対応します。 。対応する回路を紙に簡単に描くことができます。
x * x = sym_1
sym_1 * x = y
y + x = sym_2
sym_2 + 5 = out
通常、ここでの記事では、上記の方程式を R1CS の形式に整理し、特定の対応するベクトルを段階的に推定する方法を紹介します。これは、Gate を R1CS に変換する方法を理解するのに役立ちますが、この記事の中心的な目的ではありません。したがって、ここでは百の言葉が省略されています。
命題に関連付けられた変数は以下で定義されます。最初に作成されるプロトボードは、libsnark の重要な概念です。名前が示すとおり、これは回路を迅速に構築するために使用されるプロトタイプ ボードまたはブレッドボードです。zk-SNARKs 回路では、すべての変数、コンポーネント、および制約。次のコードは、外部入力と中間変数を必要とするすべての変数を定義します。
// Create protoboard
protoboard
// Define variables
pb_variable
pb_variable
pb_variable
pb_variable
pb_variable
次に、各変数をプロトボードに接続します。これは、各コンポーネントを「ブレッドボード」に挿入するのと同じです。 assign() 関数の 2 番目の文字列型変数は、DEBUG 中のコメントにのみ使用され、DEBUG 中にログを表示するのに便利です。
out.allocate(pb, "out");
x.allocate(pb, "x");
sym_1.allocate(pb, "sym_1");
y.allocate(pb, "y");
sym_2.allocate(pb, "sym_2");
pb.set_input_sizes(1);
ここでの pb への最初の接続は out 変数であることに注意してください。 zk-SNARK にはパブリック入力とプライベート監視の概念があり、それぞれ libsnark の主変数と補助変数に対応することがわかっています。では、コード内でどのように区別すればよいのでしょうか? set_input_sizes(n) を使用して、プロトボードに接続されているパブリック/プライマリ変数の数 n を宣言する必要があります。ここで n = 1 は、pb に接続されている最初の n = 1 個の変数がパブリックであり、残りがプライベートであることを示します。
これまでのところ、すべての変数がプロトボードに正常に接続されています。次に決定すべきことは、これらの変数間の制約関係です。これもわかりやすいのですが、同様の部品をブレッドボードに挿入した後、回路要件に応じてそれらの関係を決定し、接続してはんだ付けする必要があります。次のようにプロトボードの add_r1cs_constraint() 関数を呼び出して、a * b = c の形式の r1cs_constraint を pb に追加します。つまり、r1cs_constraint
// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint
// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint
// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint
// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint
ここまでで、変数間の制約も追加され、命題の回路が構築されました。前述の「4 つのステップ」の 2 番目のステップに入りましょう。生成アルゴリズム (G) を使用して、命題、つまり信頼できるセットアップの公開パラメーター (pk および vk) を生成します。生成された証明キーと検証キーは、それぞれ keypair.pk と keypair.vk を通じて取得できます。
const r1cs_constraint_system
const r1cs_gg_ppzksnark_keypair
3 番目のステップに進み、証明書を生成します。まず、一般の意見と証人として具体的な値を提供します。 x = 3、out = 35 が元の方程式の解であることを理解するのは難しくありません。次に、x、out、および各中間変数に順番に値を割り当てます。
pb.val(out) = 35;
pb.val(x) = 3;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;
次に、パブリック入力と証人の値を証明のために証明者関数に渡します。これには、それぞれ pb.primary_input() と pb.auxiliary_input() を通じてアクセスできます。生成されたプルーフはプルーフ変数とともに保存されます。
const r1cs_gg_ppzksnark_proof
最後に、verifier 関数を使用して証明を検証します。 Verified = true の場合、証明の検証は成功です。
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC
ログ出力から、検証結果は true、R1CS 制約の数は 4、パブリック入力とプライベート入力の数はそれぞれ 1 と 4 であることがわかります。ログ出力は期待どおりです。
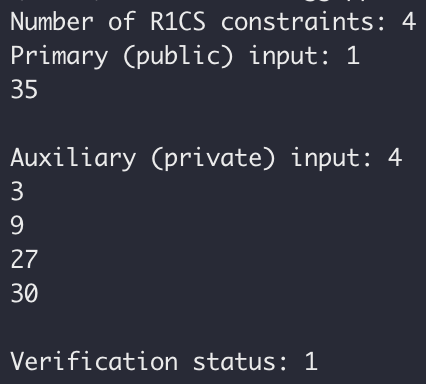
実際のアプリケーションでは、信頼できるセットアップ、証明、検証がさまざまな役割によって実行され、最終的な効果として、証明者は検証者に短い証明と公開入力を提供し、検証者は命題が真であるかどうかを自ら検証できるようになります。前の例では、証明者が秘密 x を知っていることを検証できるため、方程式の具体的な解 x を知らなくても x^3 + x + 5 = out を確立できます。
わずか数十行のコードで、学術界における zk-SNARK の最新の研究結果を簡単に操作できます。
5. もう一度実践してみる
上記の例を通じて、libsnark ライブラリを使用して zk-SNARKs 回路を開発するための重要な手順をすべて見てきました。
次に、新しい例でそれを統合しましょう。秘密の数値のサイズを明らかにせずに、数値が 60 未満であることを証明します。
通常のプログラムでは 1 つの演算子で実行できるこのことを、libsnark ではどのように表現すればよいでしょうか?
zk-SNARKs 回路開発の主な作業負荷と難しさは、命題内のすべての制約をコードで「正確に」記述する方法です。記述が「正確」でなくなると、制約が見逃されるか間違って記述され、最終的な回路が証明したい内容は元の命題から遠く離れてしまいます。前のセクションの例には単純な乗算と加算のみが含まれており、これは r1cs_constraint の最も基本的な形式と一致しているため、制約の表現は比較的簡単です。さらに、ほとんどすべての制約はあまり直観的ではなく、初心者にとって制約の詳細を正確に記述することは困難です。
幸いなことに、libsnark はすでに多くの基本的な回路ウィジェットを実装しています。すぐに使用できるガジェットが gadgetlib1 および gadgetlib2 で提供されています。中でも gadgetlib1 がよく使われており、sha256、マークルツリー、ペアリングなどの回路実装を含むハッシュ計算がまとめられています。
DangDangDang、gadgetlib1/gadgets/basic_gadgets.hpp の比較ガジェットはまさに必要なものです。
comparison_gadget(protoboard
const size_t n,
const pb_linear_combination
const pb_linear_combination
const pb_variable
const pb_variable
const std::string &annotation_prefix="")
ガジェットは多くのパラメータを渡す必要があります。n は桁数を示し、A と B は比較される 2 つの数値で、less とless_or_eq は 2 つの数値間の関係が「より小さい」か「より小さい」かをマークするために使用されます。以上」。ガジェット実装の原理は、A と B の比較を 2^n + B - A ビット単位の表現に変換するだけです。特定の実装では、他の多くの基本的なガジェットも使用されており、それらは、comparison_gadget を介して渡すことができます。
ここでは、次の変数を作成し、x と max を pb に接続し、max 値を値の上限を表す 60 に設定する必要があります。
protoboard
pb_variable
pb_variable
x.allocate(pb, "x");
max.allocate(pb, "max");
pb.val(max)= 60;
Compare_gadget を使用して cmp を作成し、前のパラメータを入力して、ガジェットに付属するgenerate_r1cs_constraints() メソッドを呼び出します。同時に、less * 1 = 1 を要求する別の制約を追加します。つまり、less が true でなければなりません。
comparison_gadget
cmp.generate_r1cs_constraints();
pb.add_r1cs_constraint(r1cs_constraint
証人 (秘密の値 x) を入力し、x = 18 とします。ここでも、comparison_gadget のgenerate_r1cs_witness メソッドを呼び出す必要があります。
// Add witness values
pb.val(x) = 18; // secret
cmp.generate_r1cs_witness();
残りは前の例と一致しています。つまり、秘密の数のサイズを明らかにすることなく、数値が 60 未満であることを証明できます。同様に、値の最大値と最小値を制限する「範囲証明」が実装されています。
強力な基本ライブラリの助けを借りて、短いコードで証明要件を達成しました。
6. What's NEXT?
これを読んだ後は、誰もが libsnark および zk-SNARKs 回路開発の使用方法について予備的に理解したと思います。
libsnark は比較的簡単に使用でき、実際の焦点は zk-SNARKs 回路開発にあることがわかったかもしれません。前述したように、コードは証明すべき命題に含まれるすべての制約を「正確に」記述するために使用する必要があり、制約が「欠落」したり、「書き間違え」たりすると、証明の内容が本来の意図とは大きく異なり、証明が無意味になってしまいます。 。
実際のビジネス ロジックを zk-SNARKs 回路コードに正しく効率的に変換する方法は、まさに開発者が継続的に研究し実践する必要があるものです。
幸いなことに、すでに libsnark 試験場があり、簡単にコードを変更して追加して試すことができます。
どんなに複雑な回路実装であっても、より単純な「回路部品」を一つ一つ組み合わせて実装することで回路を構成します。したがって、libsnark に付属する基本ライブラリは、その使用方法を学ぶだけでなく、その実装原理を学ぶためにも非常に重要な学習教材です。
また、HarryR のような他のプロジェクトの回路実装を読むことで、ZKP を実際のビジネスに適用する方法を理解することもできます。ethsnarks-miximusそしてループリングさんのprotocol3-circuits。これらのプロジェクトから、大規模な回路を設計および開発する方法や、回路のパフォーマンスに関連するさまざまな設計最適化の詳細を学ぶことができ、同時に回路の制約の規模についてより深く理解することができます。
また、Ambi Labの「ゼロ知識証明 コーディングで学ぶ libsnarkシリーズ」の続報にも引き続きご注目ください。次回はzk-SNARKとスマートコントラクトの組み合わせに挑戦していきます。回路モジュール開発、より複雑な libsnark 実装ケース、回路開発プロセス中に踏みやすい落とし穴についてはさらに説明します。
7. 付録
main.cpp
最初の例 main.cpp は、libsnark の公式サンプルのサンプル コードを呼び出します。この例を通して、libsnark の基本的な使用プロセスと主な機能を理解することができます。
#include
#include
#include
#include
using namespace libsnark;
/**
* The code below provides an example of all stages of running a R1CS GG-ppzkSNARK.
*
* Of course, in a real-life scenario, we would have three distinct entities,
* mangled into one in the demonstration below. The three entities are as follows.
* (1) The "generator", which runs the ppzkSNARK generator on input a given
* constraint system CS to create a proving and a verification key for CS.
* (2) The "prover", which runs the ppzkSNARK prover on input the proving key,
* a primary input for CS, and an auxiliary input for CS.
* (3) The "verifier", which runs the ppzkSNARK verifier on input the verification key,
* a primary input for CS, and a proof.
*/
template
bool run_r1cs_gg_ppzksnark(const r1cs_example
{
libff::print_header("R1CS GG-ppzkSNARK Generator");
r1cs_gg_ppzksnark_keypair
printf("\n"); libff::print_indent(); libff::print_mem("after generator");
libff::print_header("Preprocess verification key");
r1cs_gg_ppzksnark_processed_verification_key
libff::print_header("R1CS GG-ppzkSNARK Prover");
r1cs_gg_ppzksnark_proof
printf("\n"); libff::print_indent(); libff::print_mem("after prover");
libff::print_header("R1CS GG-ppzkSNARK Verifier");
const bool ans = r1cs_gg_ppzksnark_verifier_strong_IC
printf("\n"); libff::print_indent(); libff::print_mem("after verifier");
printf("* The verification result is: %s\n", (ans ? "PASS" : "FAIL"));
libff::print_header("R1CS GG-ppzkSNARK Online Verifier");
const bool ans2 = r1cs_gg_ppzksnark_online_verifier_strong_IC
assert(ans == ans2);
return ans;
}
template
void test_r1cs_gg_ppzksnark(size_t num_constraints, size_t input_size)
{
r1cs_example
const bool bit = run_r1cs_gg_ppzksnark
assert(bit);
}
int main () {
default_r1cs_gg_ppzksnark_pp::init_public_params();
test_r1cs_gg_ppzksnark
return 0;
}
test.cpp
2 番目の例 test.cpp。この例では、libsnark を使用して最も単純な回路を構築する方法を示します。
#include
#include
#include
using namespace libsnark;
using namespace std;
int main () {
typedef libff::Fr
// Initialize the curve parameters
default_r1cs_gg_ppzksnark_pp::init_public_params();
// Create protoboard
protoboard
// Define variables
pb_variable
pb_variable
pb_variable
pb_variable
pb_variable
// Allocate variables to protoboard
// The strings (like "x") are only for debugging purposes
out.allocate(pb, "out");
x.allocate(pb, "x");
sym_1.allocate(pb, "sym_1");
y.allocate(pb, "y");
sym_2.allocate(pb, "sym_2");
// This sets up the protoboard variables
// so that the first one (out) represents the public
// input and the rest is private input
pb.set_input_sizes(1);
// Add R1CS constraints to protoboard
// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint
// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint
// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint
// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint
const r1cs_constraint_system
// generate keypair
const r1cs_gg_ppzksnark_keypair
// Add public input and witness values
pb.val(out) = 35;
pb.val(x) = 3;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;
// generate proof
const r1cs_gg_ppzksnark_proof
// verify
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC
cout << "Number of R1CS constraints: " << constraint_system.num_constraints() << endl;
cout << "Primary (public) input: " << pb.primary_input() << endl;
cout << "Auxiliary (private) input: " << pb.auxiliary_input() << endl;
cout << "Verification status: " << verified << endl;
}
range.cpp
3 番目の例 range.cpp。この例では、libsnark に付属する比較ガジェットを使用して、値の範囲の証明を実現します。
#include
#include
#include
#include
using namespace libsnark;
using namespace std;
int main () {
typedef libff::Fr
// Initialize the curve parameters
default_r1cs_gg_ppzksnark_pp::init_public_params();
// Create protoboard
protoboard
pb_variable
pb_variable
x.allocate(pb, "x");
max.allocate(pb, "max");
pb.val(max)= 60;
comparison_gadget
cmp.generate_r1cs_constraints();
pb.add_r1cs_constraint(r1cs_constraint
const r1cs_constraint_system
// generate keypair
const r1cs_gg_ppzksnark_keypair
// Add witness values
pb.val(x) = 18; // secret
cmp.generate_r1cs_witness();
// generate proof
const r1cs_gg_ppzksnark_proof
// verify
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC
cout << "Number of R1CS constraints: " << constraint_system.num_constraints() << endl;
cout << "Primary (public) input: " << pb.primary_input() << endl;
cout << "Auxiliary (private) input: " << pb.auxiliary_input() << endl;
cout << "Verification status: " << verified << endl;
}



