はじめに：システムアーキテクチャから再現性保証まで

従来のブロックチェーンシステムでは、プルーフ・オブ・ワークはセキュリティ確保のために主にハッシュ演算のランダム性に依存しています。しかし、Gonka PoW 2.0はより複雑な課題に直面しています。それは、大規模な言語モデルに基づく計算において予測不可能な結果を保証すると同時に、誠実なノードであれば誰でも同じ計算プロセスを再現・検証できることを保証することです。この記事では、MLNodeが綿密に設計されたシードメカニズムと決定論的アルゴリズムを通じて、この目標をどのように達成しているかを詳しく解説します。

具体的な技術的実装を詳しく検討する前に、まず PoW 2.0 システム アーキテクチャの全体的な設計と、その中で再現性が果たす重要な役割を理解する必要があります。

1. PoW 2.0 システムアーキテクチャの概要

1.1 階層化アーキテクチャ設計

Gonka PoW 2.0 は、ブロックチェーン レベルから計算実行レベルまでの再現性を確保するために階層化アーキテクチャを採用しています。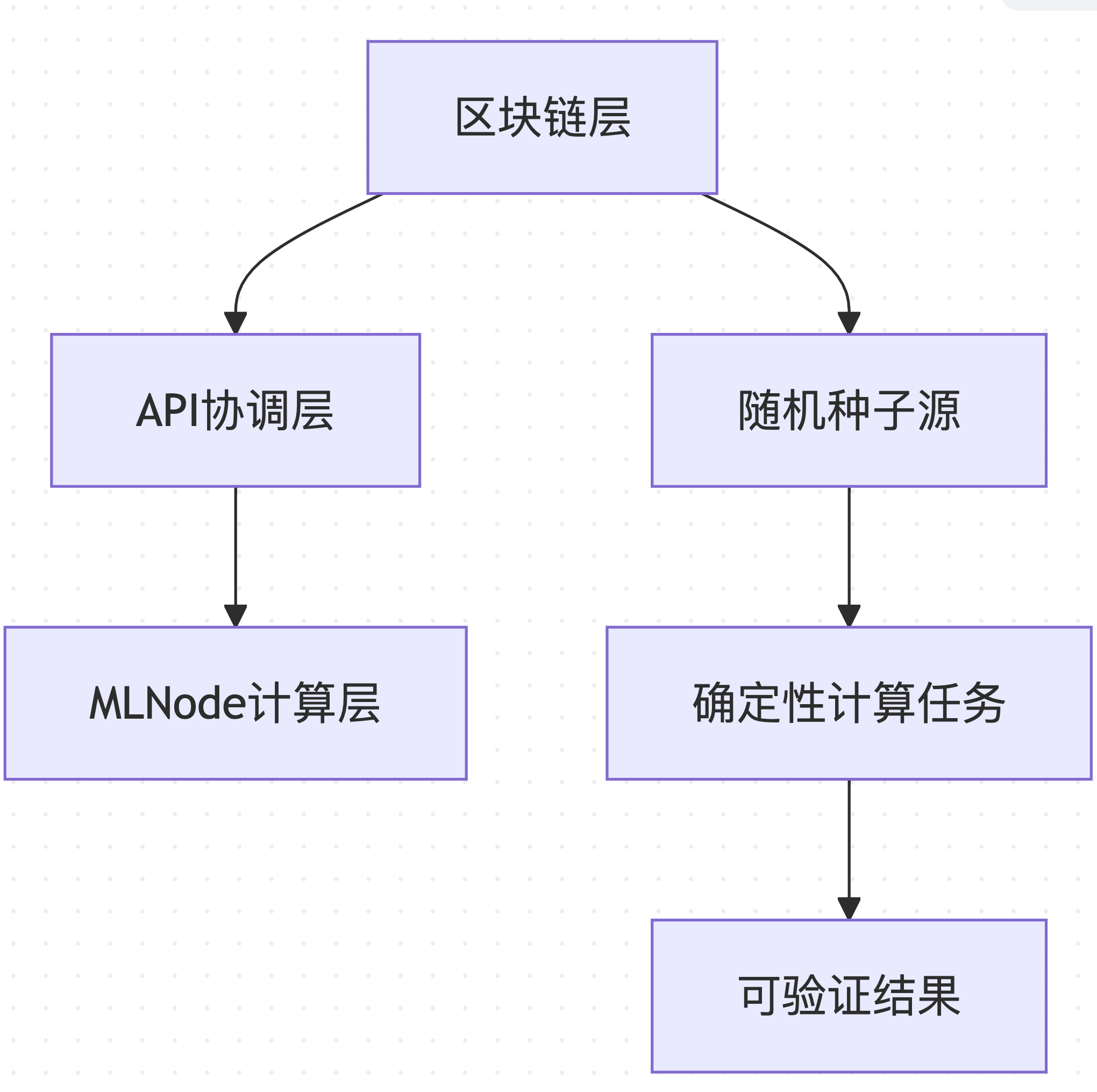

データソース: decentralized-api/internal/poc と mlnode/packages/pow のアーキテクチャ設計に基づく

この階層化設計により、全体的な一貫性と検証可能性を維持しながら、システムのさまざまなコンポーネントを個別に最適化できます。

1.2 再現性の中核目標

PoW 2.0 システムの再現性設計は、次の主要な目標を達成します。

1.計算の公平性：すべてのノードが同じ計算課題に直面することを保証する

2.結果検証: 正直なノードであれば誰でも計算結果を再現して検証できる

3.不正行為防止保証：事前計算と結果の改ざんを計算的に不可能にする

4.ネットワーク同期：分散環境における状態の一貫性の確保

これらの目標は、PoW 2.0 の再現可能な設計の基礎を形成し、システムのセキュリティと公平性を保証します。

2. シードシステム：多段階ランダム性の統合管理

システムアーキテクチャを理解した後、再現性を実現するための鍵となる技術であるシードシステムについて深く掘り下げる必要があります。このシステムは、多層的なランダム性管理を通じて、計算の一貫性と予測不可能性を保証します。

2.1 シードの種類と具体的なターゲット

Gonka PoW 2.0 は、それぞれ特定の計算目標に対応する 4 つの異なるタイプのシードを設計します。

ネットワークレベルのシード

データソース: decentralized-api/internal/poc/random_seed.go#L90-L111

目標: 各エポックでネットワーク全体に統一されたランダム性ベースを提供し、すべてのノードが同じグローバル ランダム性ソースを使用するようにします。

ネットワーク レベルのシードは、システム全体のランダム性の基盤であり、ネットワーク内のすべてのノードがブロックチェーン トランザクションを通じて同じランダム性の基盤を使用することを保証します。

タスクレベルのシード

データソース: mlnode/packages/pow/src/pow/random.py#L9-L21

目標: SHA-256 ハッシュを複数回実行してエントロピー空間を拡張し、あらゆる計算タスクに対応する高品質の乱数ジェネレーターを生成します。

タスク レベルのシードは、エントロピー空間を拡張することで、特定のコンピューティング タスクごとに高品質のランダム性を提供します。

ノードレベルのシード

データソース: シード文字列構築パターン `f"{hash_str}_{public_key}_nonce{nonce}"`

目標: 衝突や重複を防ぐために、異なるノードと異なる nonce 値が完全に異なる計算パスを生成するようにします。

ノードレベルのシードは、ノードの公開キーと nonce 値を組み合わせることで、各ノードの計算パスが一意であることを保証します。

ターゲットベクターシード

データソース: mlnode/packages/pow/src/pow/random.py#L165-L177

目標: ネットワーク全体の統一されたターゲット ベクトルを生成し、すべてのノードが同じ高次元球面位置に向けて最適化されます。

ターゲット ベクトル シードは、ネットワーク内のすべてのノードが同じ目標に向かって計算することを保証し、これが結果の一貫性を検証するための鍵となります。

2.2 種子ライフサイクル管理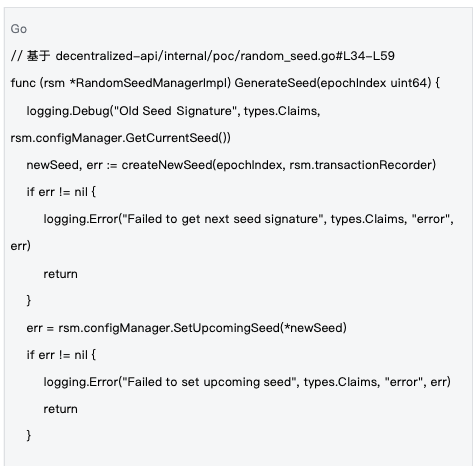

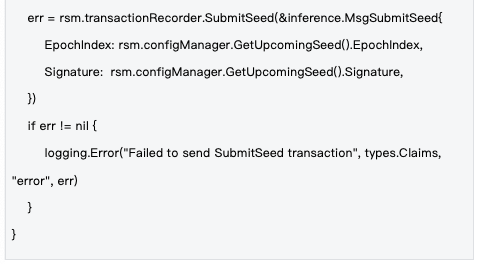
管理メカニズム：シードはエポックレベルで管理されます。各エポックの開始時に新しいシードが生成され、ブロックチェーントランザクションを通じてネットワーク全体に同期されます。これにより、すべてのノードが同じ乱数ベースを使用することが保証されます。

シードのライフサイクル管理は、ランダム性の適時性と一貫性を確保し、システムの安全な運用にとって重要な保証となります。

3. LLMコンポーネントのシード駆動型生成メカニズム

シードシステムを明確に理解できたので、次はこれらのシードをLLMコンポーネントの生成にどのように適用するかを検討する必要があります。これが再現性を実現するための鍵となります。

3.1 モデルの重みのランダム初期化

モデルの重みをランダムに初期化する必要があるのはなぜですか?

従来のディープラーニングでは、モデルの重みは通常、事前学習によって取得されます。しかし、PoW 2.0では、以下の点を確実にするために、

1.計算タスクの予測不可能性: 固定された重みのため、同じ入力では予測可能な出力が生成されない

2. ASIC耐性：専用ハードウェアは固定重量に最適化できない

3.公平な競争: すべてのノードは同じランダム初期化ルールを使用する

データソース: mlnode/packages/pow/src/pow/random.py#L71-L88

モデルの重みをランダムに初期化することは、計算の予測不可能性および公平性を確保するための重要なステップです。

重み初期化の決定論的プロセス

データソース: mlnode/packages/pow/src/pow/compute/model_init.py#L120-L125

主な特徴:

• ブロックハッシュをランダムシードとして使用し、すべてのノードが同じ重みを生成するようにします。

• 重みの初期化には正規分布N(0, 0.02²)を使用する

• メモリ最適化のためにさまざまなデータ型（float16など）をサポート

この決定論的なプロセスにより、異なるノードが同じ条件下でまったく同じモデルの重みを生成することが保証されます。

3.2 入力ベクトル生成メカニズム

なぜランダム入力ベクトルが必要なのでしょうか?

従来の PoW では固定データ (トランザクション リストなど) を入力として使用しますが、PoW 2.0 では次のことを保証するために、ノンスごとに異なる入力ベクトルを生成する必要があります。

1.探索空間の連続性：異なるナンスは異なる計算パスに対応する

2.予測不可能な結果: 入力の小さな変化が出力に大きな違いをもたらす

3.検証の効率性：検証者は同じ入力を素早く再現できる

データソース: mlnode/packages/pow/src/pow/random.py#L129-L155

ランダムな入力ベクトルを生成することで、計算の多様性と予測不可能性を確保します。

入力生成の数学的基礎

データソース: mlnode/packages/pow/src/pow/random.py#L28-L40

技術的特徴:

• 各ノンスは一意のシード文字列に対応する

• 標準正規分布を使用して埋め込みベクトルを生成する

• 効率を向上するためにバッチ生成をサポート

この数学的な基礎により、入力ベクトルの品質と一貫性が保証されます。

3.3 出力順列生成

なぜ順列を出力する必要があるのでしょうか?

LLMの出力層では、語彙は通常大規模です（例：32K～100Kトークン）。計算量を増加させ、標的を絞った最適化を防ぐため、システムは出力ベクトルをランダムに並べ替えます。

データソース: mlnode/packages/pow/src/pow/random.py#L158-L167

出力の順列により計算の複雑さが増し、システムのセキュリティが向上します。

アレンジメントの適用メカニズム

データソース: mlnode/packages/pow/src/pow/compute/compute.py の処理ロジックに基づく

設計目標:

• 計算課題の複雑さを増す

• 特定の語彙位置の最適化を防止

• 検証をサポートするために決定論を維持する

このアプリケーション メカニズムにより、取り決めの有効性と一貫性が保証されます。

4. 目標ベクトルと球面間の距離の計算

LLM コンポーネントの生成メカニズムを理解した後、PoW 2.0 の核となる計算上の課題、つまりターゲット ベクトルと球の間の距離の計算をさらに検討する必要があります。

4.1 ターゲットベクトルとは何ですか?

ターゲット ベクトルは、PoW 2.0 の計算課題の「中心」です。すべてのノードは、モデル出力をこの事前に決定された高次元ベクトルにできるだけ近づけようとします。

ターゲットベクトルの数学的性質

データソース: mlnode/packages/pow/src/pow/random.py#L43-L56

主な特徴:

• ベクトルは高次元単位球面上にある（||target|| = 1）

• 球面上の均一な分布を保証するためにマルサリア法を使用する

• すべての次元が選択される確率は等しい

ターゲット ベクトルの数学的特性により、計算課題における公平性と一貫性が保証されます。

4.2 なぜ球上で結果を比較するのか?

数学的優位性

1.正規化の利点：球面上のすべてのベクトルは単位長さを持ち、ベクトルの大きさの影響を排除します。

2.幾何学的直観：球面上のユークリッド距離は角距離に直接対応する

3.数値安定性: 大きな数値範囲によって引き起こされる計算の不安定性を回避します

高次元幾何学の特殊な性質

高次元空間（4096次元語彙空間など）では、球面分布は直感に反する特性を持ちます。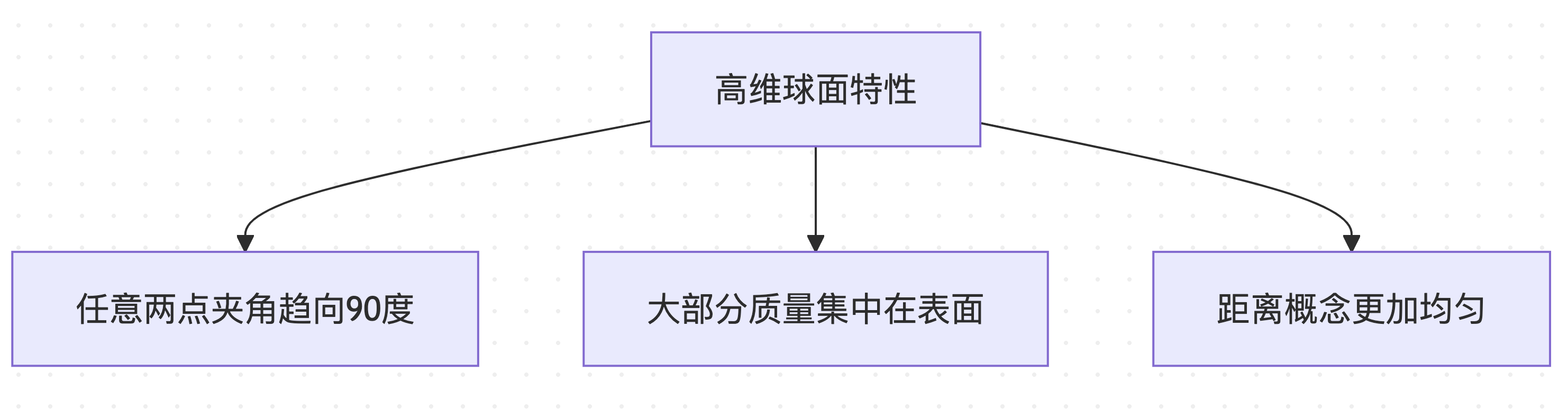

これらの特殊な特性により、球面距離の計算は計算上困難な理想的な測定基準となります。

4.3 r_target推定とPoCステージの初期化

r_targetの概念と計算

r_targetは、計算結果が「成功」となるための距離の閾値を定義する重要な難易度パラメータです。r_targetより小さい距離の結果は、有効な作業証明とみなされます。

データソース: decentralized-api/mlnodeclient/poc.go#L12-L14

Gonka PoW 2.0では、r_targetのデフォルト値は1.4013564660458173に設定されています。この値は、計算難易度とネットワーク効率のバランスをとることを目的として、広範な実験と統計分析を通じて決定されました。システムには動的な調整メカニズムが存在します。しかし、ほとんどの場合、このデフォルト値に近い値になります。

PoCフェーズでのr_targetの初期化

各 PoC (計算証明) フェーズの開始時に、システムは次のことを行う必要があります。

1.ネットワークの計算能力を評価する: 過去のデータに基づいて現在のネットワークの総計算能力を推定する

2.難易度パラメータを調整する: 安定したブロック時間を維持するために適切な `r_target` 値を設定する

3.ネットワーク全体のパラメータを同期する: すべてのノードが同じ `r_target` 値を使用していることを確認する

技術的な実装：

• r_target値はブロックチェーンの状態を通じてすべてのノードに同期されます

• 各PoCステージでは異なるr_target値が使用される可能性がある

• 適応調整アルゴリズムは、前のステージの成功率に基づいて難易度を調整します

この初期化メカニズムにより、ネットワークの安定した動作と公平性が保証されます。

5. 再現性のエンジニアリング保証

コアアルゴリズムを理解した後は、エンジニアリング実装において再現性を確保する方法に焦点を当てる必要があります。これが、実際の導入においてシステムの安定した運用を確保するための鍵となります。

5.1 決定論的コンピューティング環境

データソース: mlnode/packages/pow/src/pow/compute/model_init.py の環境設定に基づく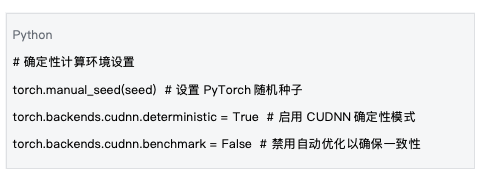

決定論的なコンピューティング環境の確立は、再現性を保証するための基礎となります。

5.2 数値精度管理

数値精度管理により、異なるハードウェア プラットフォーム上での計算結果の一貫性が保証されます。

5.3 クロスプラットフォームの互換性

システム設計では、さまざまなハードウェア プラットフォームの互換性が考慮されています。

- CPU vs GPU : CPUとGPUの両方で同じ計算結果を生成することをサポートします

-異なるGPUモデル:標準化された数値精度を通じて一貫性を確保

-オペレーティングシステムの違い: 標準の数学ライブラリとアルゴリズムを使用する

クロスプラットフォームの互換性により、さまざまな展開環境でのシステムの安定した動作が保証されます。

6. システムのパフォーマンスとスケーラビリティ

再現性を保証することに基づいて、システムは優れたパフォーマンスとスケーラビリティも備えている必要があり、これがネットワークの効率的な運用を保証する鍵となります。

6.1 並列化戦略

データソース: mlnode/packages/pow/src/pow/compute/model_init.py#L26-L53

並列化戦略は、最新のハードウェアの計算能力を最大限に活用します。

6.2 メモリの最適化

システムはさまざまな戦略を通じてメモリの使用を最適化します。

-バッチ最適化: GPU の使用率を最大化するためにバッチ サイズを自動的に調整します

-精度の選択: メモリ使用量を削減するためにfloat16を使用する

-勾配管理:推論モードでの勾配計算を無効にする

メモリの最適化により、リソースが制限された環境での効率的なシステム操作が保証されます。

要約: 再現可能な設計の工学的価値

PoW 2.0 の再現可能な設計を詳細に分析した後、その技術的成果とエンジニアリングの価値をまとめることができます。

コア技術の成果

1.マルチレベルシード管理：ネットワークレベルからタスクレベルまでの完全なシードシステムにより、コンピューティングにおける決定論と予測不可能性のバランスを確保します。

2. LLMコンポーネントの体系的ランダム化：モデルの重み、入力ベクトル、出力順列の統一ランダム化フレームワーク

3.高次元幾何学の工学的応用：球面幾何学的特性を用いた公平なコンピューティング課題の設計

4.クロスプラットフォームの再現性:標準化されたアルゴリズムと精密制御により、異なるハードウェアプラットフォーム間での一貫性を確保

これらの技術的成果が組み合わさって、PoW 2.0 の再現可能な設計の中核を形成します。

システム設計の革新的な価値

Gonka PoW 2.0は、ブロックチェーンのセキュリティを維持しながら、計算リソースを無意味なハッシュ演算から価値あるAI計算へと移行することに成功しています。再現可能な設計は、システムの公平性とセキュリティを確保するだけでなく、将来の「意味のあるマイニング」モデルのための実用的な技術的パラダイムを提供します。

技術的な影響:

• 分散AIコンピューティングのための検証可能な実行フレームワークを提供します

• 複雑なAIタスクとブロックチェーンのコンセンサスの互換性を実証

• 新しいタイプのプルーフ・オブ・ワークの設計基準を確立

Gonka PoW 2.0は、慎重に設計されたシードシステムと決定論的アルゴリズムを通じて、従来の「廃棄物ベースのセキュリティ」から「価値ベースのセキュリティ」への根本的な転換を実現し、ブロックチェーン技術の持続可能な発展への新しい道を切り開きます。

注: この記事はGonkaプロジェクトの実際のコード実装に基づいています。すべてのコード例と技術説明は、プロジェクトの公式コードリポジトリから提供されています。

Gonka.aiについて

Gonkaは、効率的なAIコンピューティングパワーを提供するために設計された分散型ネットワークです。その設計目標は、グローバルなGPUコンピューティングパワーを最大限に活用し、有意義なAIワークロードを完了することです。中央集権的なゲートキーパーを排除することで、Gonkaは開発者や研究者にコンピューティングリソースへのパーミッションレスなアクセスを提供し、参加者全員にネイティブGNKトークンを報酬として提供します。

Gonkaは、米国のAI開発会社Product Science Inc.によってインキュベートされました。Web 2業界のベテランであり、Snap Inc.の元コアプロダクトディレクターであるLibermans兄弟によって設立された同社は、2023年にOpenAIの投資家であるCoatue Management、Solanaの投資家であるSlow Ventures、K5、Insight、Benchmark Partnersなどの投資家から1,800万ドルの資金調達に成功しました。プロジェクトの初期段階からの貢献者には、6 Blocks、Hard Yaka、Gcore、Bitfuryなど、Web 2-Web 3分野の著名なリーダー企業が含まれています。

公式サイト| Github | X | Discord |ホワイトペーパー|経済モデル|ユーザーマニュアル