序文

序文

イーサリアム仮想マシンは、イーサリアム ブロックチェーン上に構築されたコード動作環境です。コントラクト コードは外部から完全に隔離され、EVM 内で実行できます。その主な機能は、イーサリアム システム内でスマート コントラクトを処理することです。イーサリアムがチューリング完成である理由は、開発者が Solidity 言語を使用して EVM 上で実行されるアプリケーションを作成でき、すべての計算可能な問題を計算できるためです。しかし、チューリングの完全性だけでは十分ではなく、EVM を ZK 証明システムにカプセル化しようとする人もいますが、問題は、カプセル化する際に多くの冗長性が生じることです。 Fox が発明した「スモール テーブル モード」zkEVM は、ネイティブの Solidity Ethereum 開発者が zkEVM にシームレスに移行できることを保証するだけでなく、EVM を ZK プルーフ システムにカプセル化するための余分なコストも大幅に削減します。

EVM は 2015 年の開始以来、壮大な ZK 変革を遂げています。この大きな変革には 2 つの主な方向性があります。

最初の方向は、いわゆる zkVM トラックです。このトラック プロジェクトは、アプリケーションのパフォーマンスを最適に改善することに特化しており、イーサリアム仮想マシンとの互換性は主な考慮事項ではありません。ここには 2 つのサブ方向性があります。1 つは独自の DSL (ドメイン固有言語) を作成することです。たとえば、StarkWare はカイロ言語の普及に取り組んでいますが、これは普及が容易ではありません。 2 つ目は、目標が既存の比較的成熟した言語と互換性があることです。たとえば、RISC Zero は zkVM を C++/Rust と互換性を持たせることに取り組んでいます。このトラックの難しさは、命令セット ISA の導入により、最終出力の制約がより複雑になっていることです。

2 番目の方向は、いわゆる zkEVM トラックです。このトラック プロジェクトは、EVM バイトコードの互換性、つまり、バイトコード レベルの EVM コードと、何よりも ZkEVM を通じて対応するゼロ知識証明を生成することに特化しています。 zkEVM への移行は無料で可能になります。このトラックのプレイヤーには主に Polygon zkEVM、Scroll、Taiko、Fox が含まれます。このトラックの難点は、EVM の冗長コストと互換性があることであり、ZK プルーフ システムでのカプセル化には適していません。長い思考と議論の末、Fox は最終的に、第 1 世代 zkEVM の膨大な冗長性を根本的に削減する鍵である「スモール テーブル モード」zkEVM を発見しました。

データ回路と証明回路は、証明を生成するための zkEVM の 2 つのコア要素です。一方、zkEVM では、証明者はトランザクションによってもたらされた状態転送が正しいことを証明するためにトランザクションに含まれるすべてのデータを必要としますが、EVM 内のデータは大きく複雑です。したがって、証明に必要なデータをどのように整理して整理するかは、効率的なzkEVMを構築するために慎重に検討する必要がある問題です。一方で、一連の回路制約を通じて計算実行の妥当性と正しさをどのように効率的に証明（または検証）するかが、zkEVM のセキュリティを確保するための基礎となります。

画像の説明

図 1: 大規模テーブルと小規模テーブル向けの 2 世代の zkEVM ソリューション

たとえば、スタック内の要素の各変更をまとめたり、スタック回路の証明を特別に作成したり、純粋な算術演算のための算術回路のセットを作成したりするなどです。このようにして、各回路が考慮する必要がある状況は比較的単純になります。これら機能の異なる回路はzkEVMごとに名称が異なり、直接回路と呼ぶ人もいれば、（サブ）ステートマシンと呼ぶ人もいますが、考え方の本質は同じです。

これを行う意味をより明確に説明するために、加算演算 (スタックの上位 2 つの要素を取り出し、それらの合計をスタックの先頭に戻す) を証明したいと仮定して、例を挙げてみましょう。

元のスタックが [ 1, 3, 5, 4, 2 ] であると仮定します。

次に、分類して分割しない場合、上記の操作の後、スタックが [ 1, 3, 5, 6 ] になることを証明する必要があります。

分類が分割されている場合は、次のことを個別に証明するだけで済みます。

スタック回路:

C 1 : [ 1, 3, 5, 4, 2 ] が 2 と 4 をポップして [ 1, 3, 5 ] になることを証明します。

C 2 : [ 1, 3, 5 ] は、push(6) 後に [ 1, 3, 5, 6 ] になることを証明します。

演算回路：

C 3 ：a= 2, b= 4,c= 6 、 a+b=c であることを証明する

画像の説明

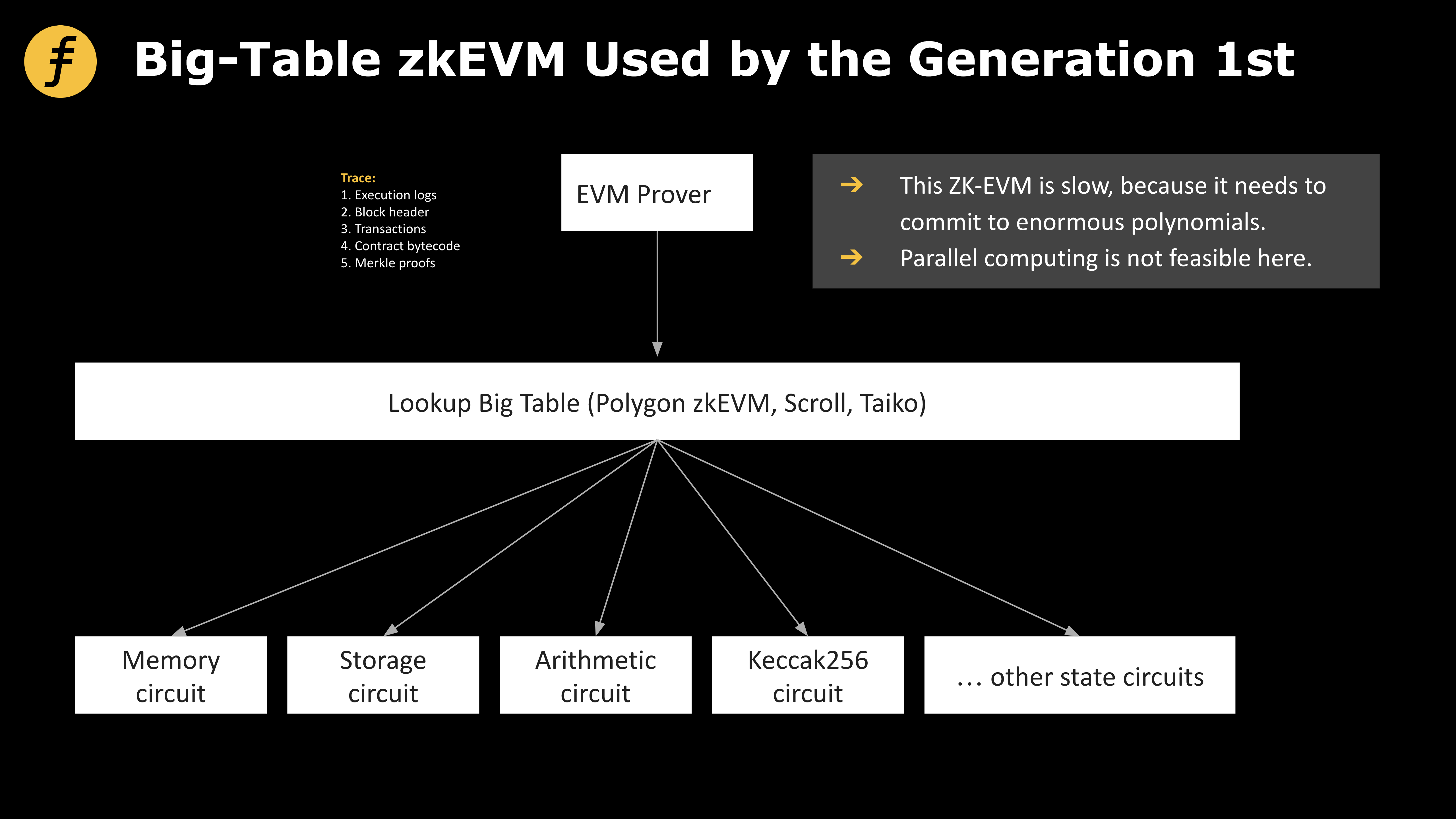
図 2: 第 1 世代の zkEVM で採用された大規模テーブル モデル

分類が分かれば、それぞれの部分の状況が比較的単純になるため、証明の難易度は大幅に下がります。

しかし、分類と分割は、異なるタイプの回路のデータの一貫性の問題という他の問題も引き起こす可能性があります。たとえば、上記の例では、実際には次の 2 つのことを証明する必要があります。

C 4 : 「C 1 でポップされた数字」 = 「C 3 の a と b」

C 5 : 「C 2 のプッシュ数」 = 「C 3 の c」

この問題を解決するために、最初の質問、つまりトランザクションに関係するデータをどのように整理するかに戻り、次にこのトピックについて説明します。

直感的な方法は次のとおりです。トレースを通じて、すべてのトランザクションに含まれる各ステップを逆アセンブルし、関係するデータを把握し、トレースに含まれていないデータの部分を取得するリクエストをノードに送信します。次のように大きなテーブル T に配置されます。

「第一段階の操作」 「第一段階の操作に関係するデータ」

「第 2 段階の操作」 「第 2 段階の操作に関係するデータ」

...「n 番目のオペレーション」「n 番目のオペレーションに関係するデータ」

したがって、上記の例では、次のような行が記録されます。

「ステップ k: 加算」 「a= 2、b= 4、c= 6」

そして、上記の C 4 は次のように証明できます。

C 4(a): C 1 によってポップされた数値は、大きなテーブル T の k 番目のステップと一致します。

C 4(a): C 3 の a と b は、大きなテーブル T のステップ k と一致します。

画像の説明

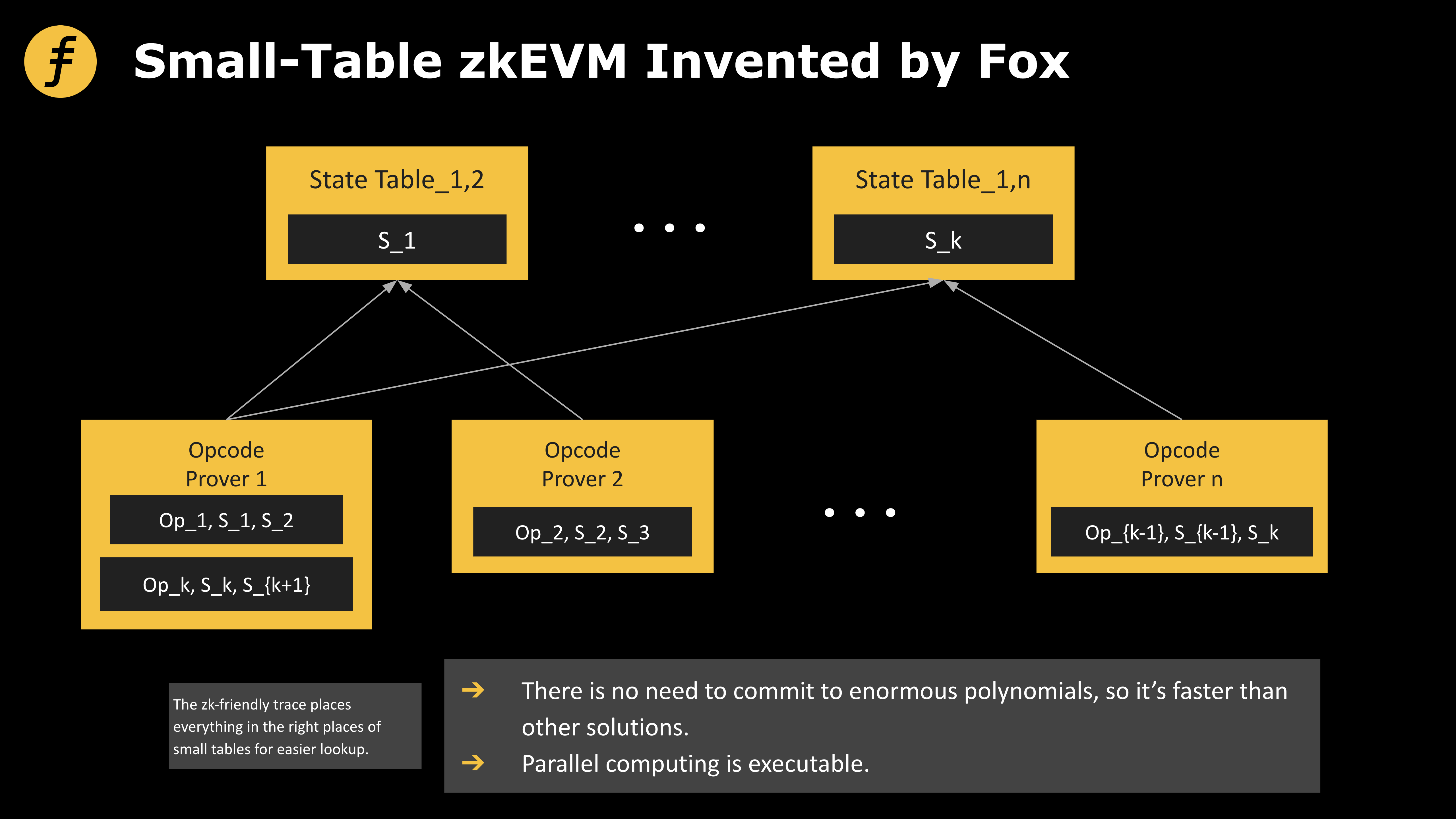
図 3: Fox が考案した「スモール テーブル モード」zkEVM

次の一連のテーブル構造を検討します。

フォームタ:

「タイプaの最初の操作」 「タイプaの最初の操作に関係するデータ」

「タイプ a の 2 番目の操作」 「タイプ a の 2 番目の操作に関係するデータ」

...「タイプ a の m 回目の操作」「タイプ a の m 回目の操作に含まれるデータ」

フォームTb:

「タイプ b の最初の操作」 「タイプ b の最初の操作に関係するデータ」

「タイプ b の 2 回目の操作」 「タイプ b の 2 回目の操作に関係するデータ」

...「タイプ b の m 回目の操作」「タイプ b の n 回目の操作に含まれるデータ」

…このように複数の小テーブルを構築すると、必要なデータの操作内容に応じて対応する小テーブルを直接参照できるため、効率が大幅に向上するというメリットがあります。

簡単な例 (一度に 1 つの要素しか検索できないと仮定します) は、[a, b, c, d, e, f, g, h] に a ～ h の 8 文字が存在することを証明したい場合、次のようになります。サイズ 8 のテーブルに対して 8 回のルックアップを実行する必要がありますが、テーブルを [a, b, c, d] と [e, f, g, h] に分割する場合、必要なのは 4 回のルックアップを実行するだけで十分です。それぞれテーブル！

結論は

結論は

Fox が発明した「スモール テーブル モード」zkEVM は、ネイティブの Solidity Ethereum 開発者が無料で zkEVM に移行できることを保証するだけでなく、EVM を ZK プルーフ システムにカプセル化するための余分なコストも大幅に削減します。これはzkEVMの構造における大きな変更であり、イーサリアムの拡張計画に大きな影響を与えるでしょう。