ゼロ知識証明におけるサムチェックプロトコルを理解するための 1 つの記事
原文著者:Fox Tech CEO Kang Shuiyue、Fox Tech主任研究員Meng Xuanji
原文著者:Fox Tech CEO Kang Shuiyue、Fox Tech主任研究員Meng Xuanji
ビットコイン、ブロックチェーン、スマートコントラクトなどの概念の普及に伴い、Web3分野の活発な発展に注目する人が増えています。テクノロジーの観点から見ると、多くの開発者は、基盤となるブロックチェーンをサポートする暗号プロトコルにも注目しています。中でもゼロ知識証明プロトコルは独自の特徴を発揮し、プライバシー保護の実現やレイヤー2の性能拡張を実現するzkrollupプロジェクトにおいて重要な役割を果たしています。
ゼロ知識証明は、アルゴリズムのクラスの総称であり、研究者はこれまでに、Plonk、Groth 16、zkStark、Virgo、Orion、Foaks などを含む多くのプロトコルを発明してきました。異なるプロトコルは異なるコンピューティングシナリオに適しており、複雑さと効率も異なります。たとえば、Foaks には線形証明時間と短い証明長という利点があります。
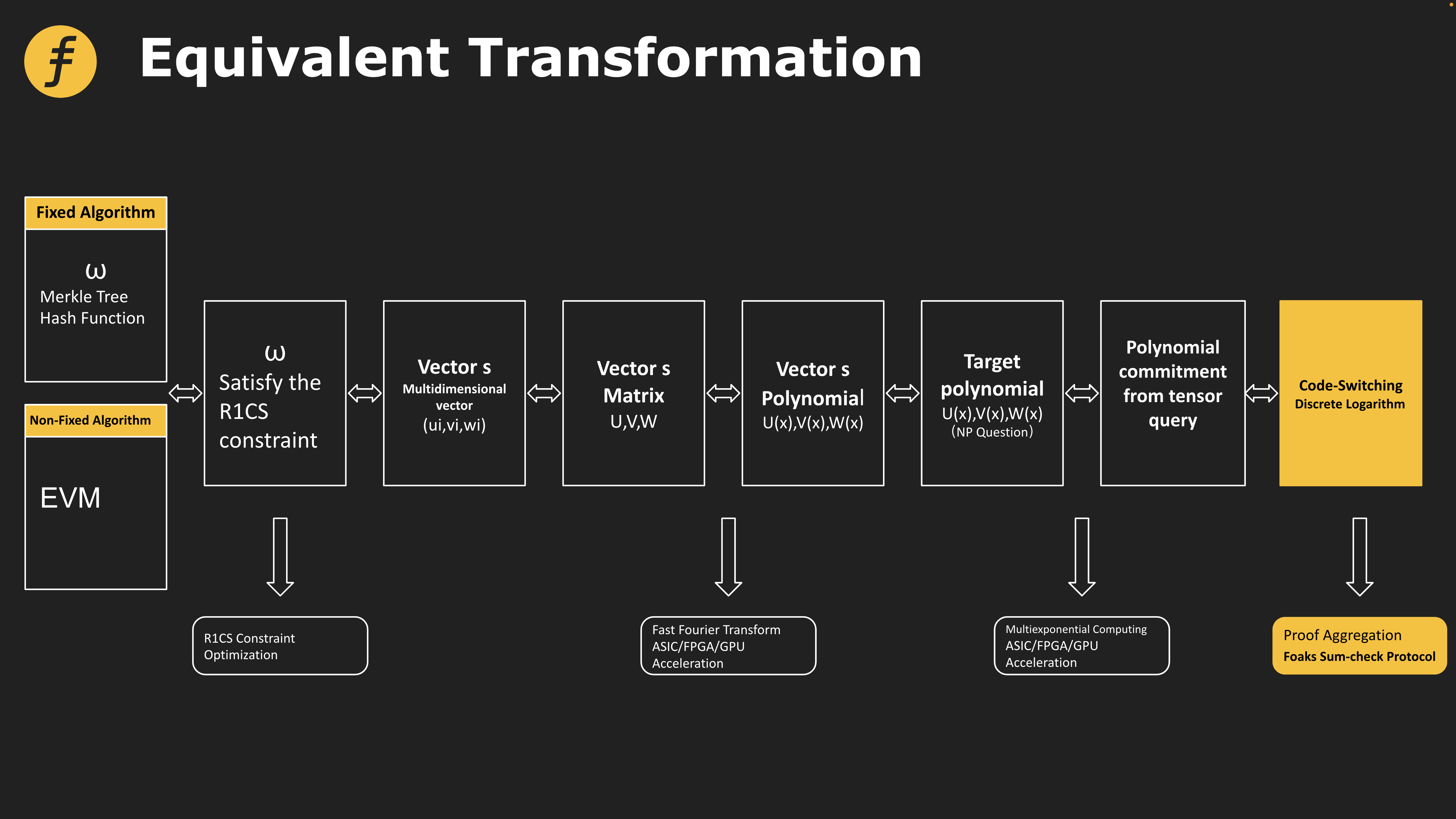
このプロトコルは、Fox Tech が採用している Foaks 証明システムでも重要な役割を果たしています。具体的には、オペコードの正しさを証明するには、まず演算回路に変換し、次に行列に変換し、最後に多項式を生成し、証明システムのアルゴリズムを多項式に適用し、最後に演算コードを圧縮する必要があります。証明の一部 このうち、証明者(Prover)と検証者(Verifier)との間の対話的な処理も、ある和を計算する処理、すなわちサムチェックプロトコルの処理に変換される。
最初のレベルのタイトル
Sum-check Protocol
副題
1. プロトコルの目的
このプロトコルの目標は非常にシンプルで理解しやすいものです。
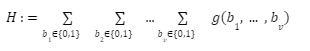
zkRollup で検討した「計算委託」シナリオと同様に、アプリケーションでは上記式の計算量が非常に多くなりますので、この式の計算を証明者 (Prover) に引き渡し、証明者が計算を行うことを考えています。計算結果が正しいことを証明するために検証者(Verifier)に報告します。
副題
2. プロトコルの前提条件
まず第一に、このプロトコルにおける検証者の機能を明確にする必要があります。検証者は関数 g を計算できるオラクル (Oracle) を持っていると仮定します。つまり、検証者が何らかの入力 r 1, ... , rv を決定した後、g(r 1, ... , rv) を計算するのは簡単です。しかし、完全な結果 H を計算するのは困難です。
2 番目の点は、プロトコルの目標に関して、実際、サムチェック プロトコルは任意のセット B に対して bBmg(b) を計算できますが、一般性を失うことなく、B={0, 1} と仮定します。
副題
3. プロトコルプロセス
この契約には合計 v ラウンドが含まれます。 g の 1 つの変数が各ラウンドで処理されます。
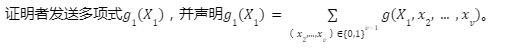
ラウンド1:
証明者が正直であれば、H=g 1(0)+g 1(1)が成立するはずである。検証者が検証し、合格した場合、乱数 r 1 が選択されて認証者に送信されます。プロトコルの前提に従って、証明者は上記の検証を完了できることに注意してください。
degi(p) を使用して、多変量多項式 p の i 番目の変数の次数を示します。 g 1(X 1) の次数は deg 1(g) であるため、g 1 は deg 1(g)+1 領域要素で表すことができることがわかります。
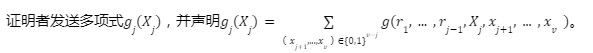
ラウンド j (j>1):
ラウンドv:
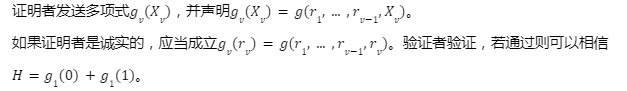
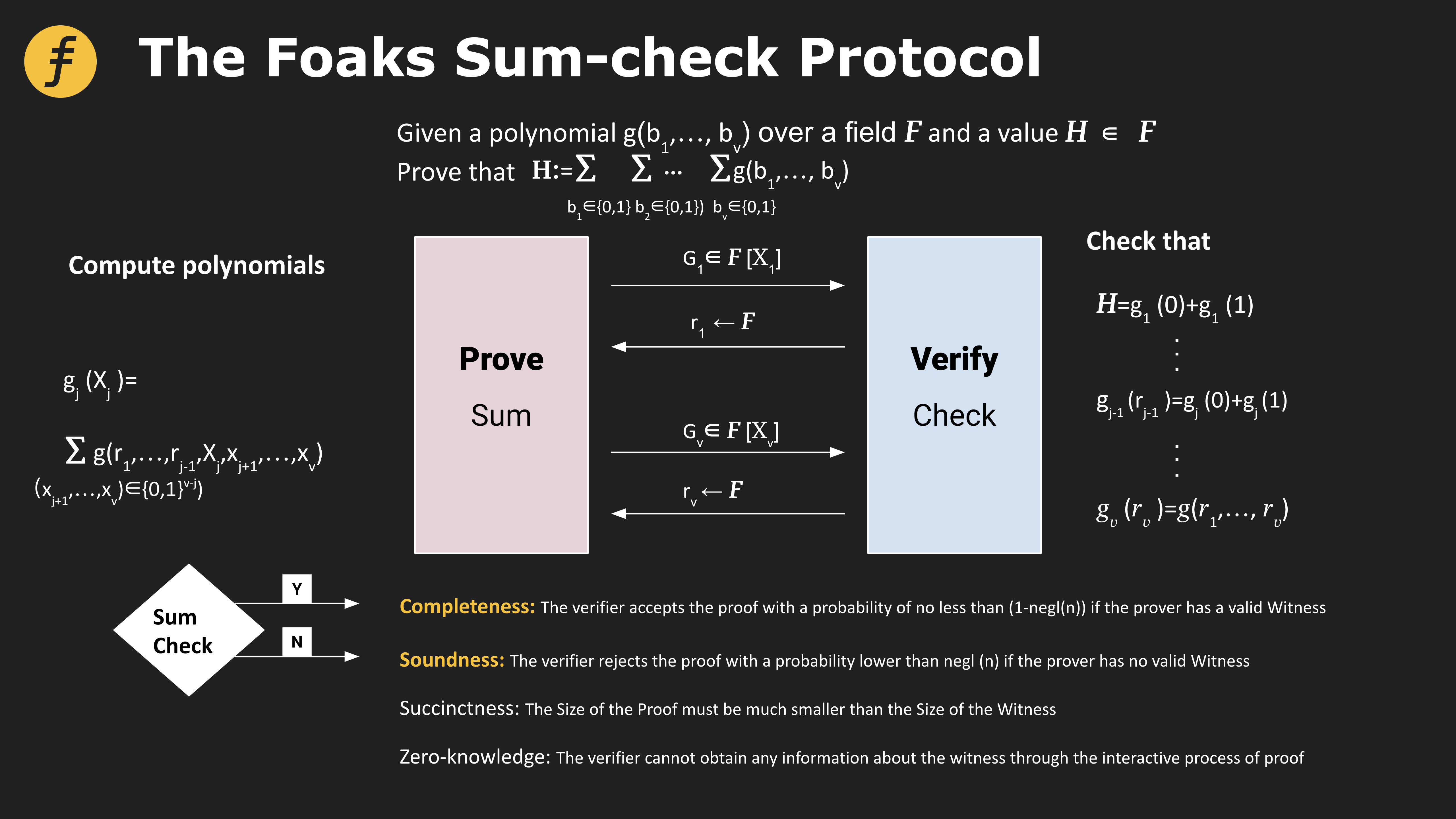
画像の説明
図 2: Foaks Sum-check プロトコル
完全性: 証明者に有効な証人がいる場合、検証者は (1-negl(n)) 以上の確率で証明を受け入れます。
健全性: 証明者に有効な証人がいない場合、検証者は negl(n) よりも低い確率で証明を拒否します。
簡潔さ: 証拠のサイズは証人のサイズよりもはるかに小さくなければなりません。
# ここで、negl(n) は無視できる関数です
副題
4. プロトコルの複雑さ
次の表は、複雑さの結果の詳細を示しています。ここで、 T は、オラクル (Oracle) にアクセスする、つまり g を 1 回評価するのに必要なオーバーヘッドを表します。

図 3: サムチェック プロトコルの複雑さ
最初のレベルのタイトル
サムチェックプロトコルの適用
多くのゼロ知識証明アルゴリズムの中で、サムチェックプロトコルは重要な役割を果たしています。多くの問題の証明は、元の問題をサムチェック形式に変換し、その後の手順を完了することにかかっています。
たとえば、サムチェック プロトコルを使用して、無向グラフ内の三角形の数をカウントできます。
まず、隣接行列 A を使用して無向グラフ G を表します。E をそのエッジ セットとし、Ai, j= 1(i, j)E、つまり、点 i、j の間にエッジがある場合、とします。その場合、Ai、j = 1、それ以外の場合は 0。点 i、j、k について、三角形を形成する 3 点の条件は Ai, j= 1, Ai, k= 1, Aj, k= 1 です。

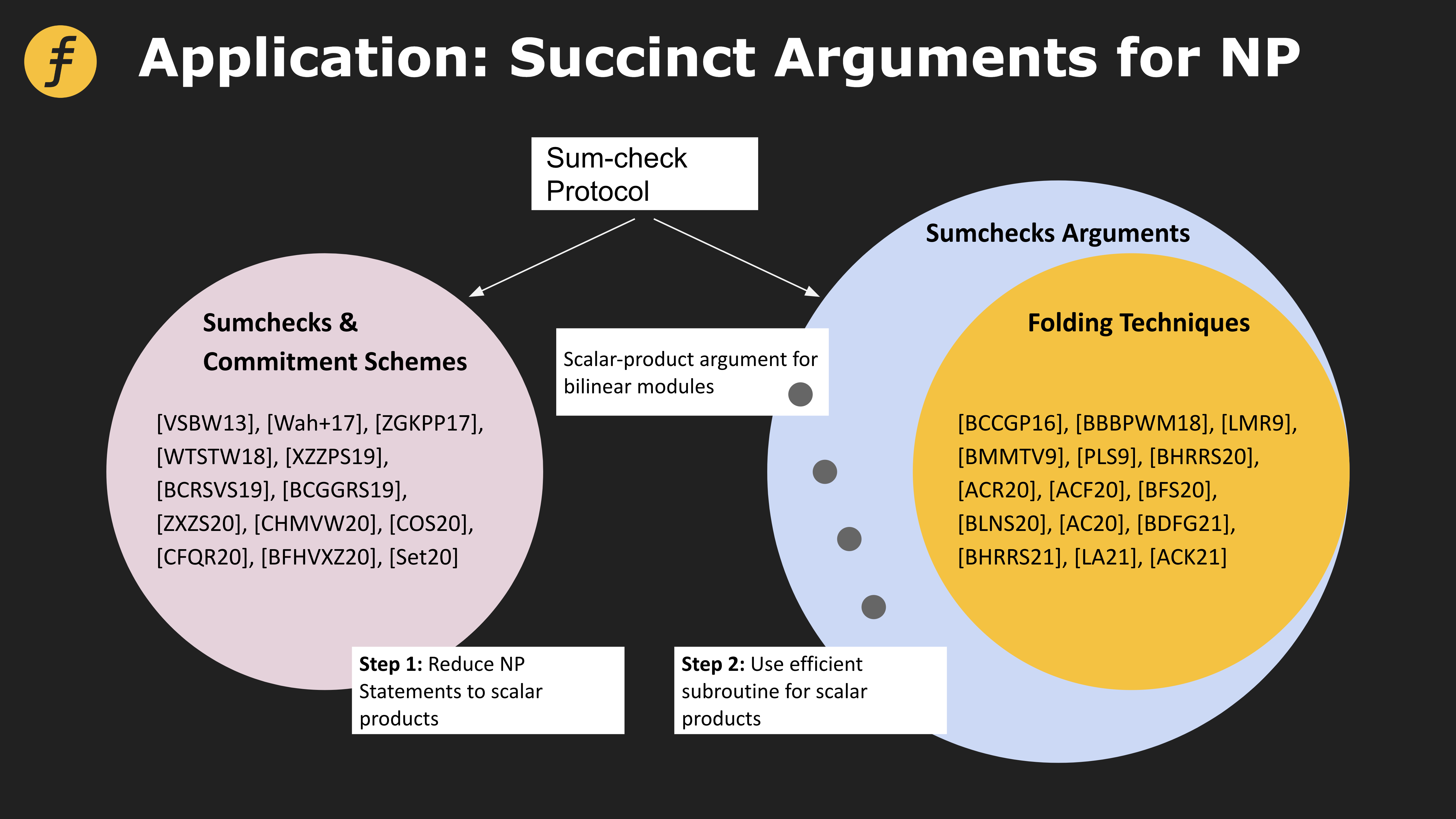
さらに、多くの証明システムでは、サムチェック プロトコルが構築の基礎となるロジックとして使用されます。以下の図は、サムチェックに基づくさまざまな変換に基づくさまざまな証明システムを示しています。

図 4: 4 種類の証明システムにおける Sum-check プロトコルの適用
最初のレベルのタイトル
エピローグ
エピローグ
最初のレベルのタイトル
参考文献
[LFKN 92 ] Carsten Lund, Lance Fortnow, Howard Karloff, and Noam Nisan. Algebraic methods for interactive proof systems. J. ACM, 39: 859 – 868, October 1992.
https://people.cs.georgetown.edu/jthaler/sumcheck.pdf
参考文献https://blog.csdn.net/mutourend/article/details/111610754



