DAOrayaki: 偽の zkSNARK プルーフの作成

DAOrayaki

特邀专栏作者

2021-12-28 12:05

この記事は約2559文字で、全文を読むには約4分かかります

zkSNARK は、ゼロ知識証明を作成する方法です。具体的には、ゼロ知識証明を作成するための簡潔で非対話型の方法です。

DAOrayaki DAOリサーチボーナスプール:

ファンディングアドレス: DAOrayaki.eth

DAOrayaki DAOリサーチボーナスプール:

ファンディングアドレス: DAOrayaki.eth

投票経過: DAO委員会2/0可決

研究タイプ: ブロックチェーンゼロ知識証明

zkSNARK は、ゼロ知識証明を作成する方法です。具体的には、ゼロ知識証明を作成するための簡潔で非対話型の方法です。

原作者: コビ・グルカン

zkSNARK は、ゼロ知識証明を作成する方法です。具体的には、ゼロ知識証明を作成するための簡潔で非対話型の方法です。

https://z.cash/technology/zksnarks/

zkSNARKsとは具体的には次のことを指します

1. Zcash での zkSNARK の構築方法 - Zcash チームの提供。

https://qed-it.com/trustless-computing-on-private-data/

2. プライベートデータのトラストレスコンピューティング - QED-it の主任暗号学者である Daniel Benarroch 氏と Aviv Zohar 氏

教授のブログ投稿。

https://qed-it.com/2017/07/04/zkp-in-action/

3. 証拠、ブロックチェーン。 ZKPinAction - ZKP と数独用の ZKP の作成方法を説明するセッション

https://qed-it.com/2017-12-20-the-incredible-machine/

ビデオ。

https://qed-it.com/2017/07/11/the-hunting-of-the-snark/

4. 信じられないほどのマシン - QED-it の主任研究員である Aviv Zohar 教授による、信じられないほどの設定を説明するブログ投稿。

5. Hunting SNARK - ZKP を実験するための一連の謎。

QED-it では、zkSNARK やその他のツールを使用して、企業向けのゼロ知識ブロックチェーンを作成します。

おそらく、zkSNARK の実稼働環境で最もよく知られているのは ZCash です。ZCash は、リンクできないトランザクションと金額が隠された暗号通貨です。 ZCash および zkSNARK を利用する他のいくつかの製品は、Pinnochio と呼ばれる構造に基づいていますが、より具体的には BCTV14a です。ご想像のとおり、これは素晴らしいテクノロジーです。この構造には、信頼できるセットアップという明らかな欠点があります。"信頼できる設定"セットアップは、CRS (Common Reference String)、または証明書キーと検証キーのペアとして広く知られているものを生成するプロセスです。これら

鍵"証明者と検証者は、それぞれ特定の問題 (または制約システム) の証明を生成および検証するために使用されます。"このプロセス中に、いくつかのランダムな要素がサンプリングされますが、秘密にしておく必要があります。なぜなら、検証者がこれを知っていれば、証明プロセスで問題に対する実際の解決策を使用せずに、正常に検証された証明を作成できるからです。言い換えれば、証拠を改ざんし、健全性を損なうことです。このランダム性は次のようにも知られています。

。単一のエンティティを信頼しないことで、この懸念を回避する方法があります。公共回線の場合、これらの方法には通常、複数の参加者がランダム性を提供するマルチパーティ計算が含まれますが、ランダム性は後で破棄されます。興味深いことに、参加者の 1 人が正直であり、そのランダム性が破壊されている限り、プロセス全体は安全です。

1. "The Ceremony "ポッドキャスト

https://www.wnycstudios.org/podcasts/radiolab/articles/ceremony

MPC を使用した信頼できるセットアップの注目すべき例としては、ZCash があります。

https://z.cash.foundation/blog/powers-of-tau/

ポッドキャスト"Tau"2.タウの力

ここでこれがポップアップ表示されることに気づくかもしれません

...タウの秘密は非常に重要です。タウが証明者に知られると、証明を偽造するのは簡単になります。

証明書を作成する

BCTV14a で提案されている構造を簡単に見てみましょう。"これは数学の問題なので、この記事に関連する詳細を抜粋してみましょう。"1. タウは、セットアップ中にランダムに描画される有限フィールド内の点であり、

有毒廃棄物"a*b=c "その一部。"a*b-c=0"。

2. 証明中、検証者は制約システムの解とパブリックおよびプライベート入力からいくつかの多項式 - A(z)、B(z)、および C(z) を計算します。基本的に、これらの多項式は次のことを表します。"フォームの制約、または同等の制約"H(z)--H(Tau)。

3. 検証者は、H(z)=(A(z)B(z)-C(z))/Z(z) も計算します。ここで、Z(z) は、制約システムをゼロに表す点における公開多項式です。 A、B、および C は検証者の入力を考慮するため、分子も同じ点でゼロに設定されている場合にのみ H を計算できることに注意してください。これは、検証者が A*BC =0 をもたらす問題の解を実際に知っていることを証明します。。ここで重要な部分が始まります - 検証者はタウを知らなくても計算できます

インデックス内で

なぜこれを行うのでしょうか?なぜなら、証明者はランダムな点 Tau で評価することにより、方程式 H=(A*BC)/Z がすべての Z に対して成り立つことを示す確率が高いからです。同じ問題を別の観点から見ると、タウを知らなければ、証明者は、その時点でまったく同じ値を生み出す多項式を高い確率で生成することができません。

技術的にこれをどのように行うのでしょうか?セットアップ手順の一部で、pk_Hi として与えられる、指数に隠されたタウの関連するすべての累乗を含む要素が生成されるという事実があります。 H の係数があれば、これらを組み合わせて H(Tau) を作成できます。

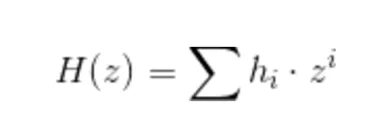
すなわち

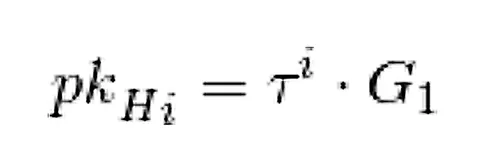
検証者によって計算された H(z)

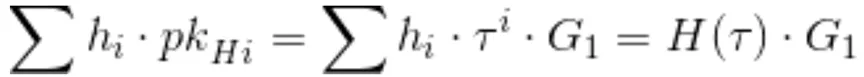
構成証明から取得されたキー、セットアップ中に計算されたキー

H(タウ) の「指数内」評価

証明を受け取った後、検証者は、関係 H=(A*BC)/Z を満たす H の係数を実際に提供したかどうかを指数で再度チェックできます。これは、検証者が実際に解を知っている場合にのみ実行できます。

偽造された証明書

ここで仮説を立ててみましょう。タウが知られている場合はどうなるでしょうか?何らかの理由でセットアップ中に公開され、悪意のあるバリデータに知られた場合。

明らかに、証拠を偽造するのは非常に簡単です。 H=(A*BC)/Z の等価性チェックは特定の点タウで行われるため、タウについての既知の情報を使用して、完全に満たす多項式を作成できます。つまり、常に (A(Tau)*B(Tau)-C(Tau))/Z(Tau) を返す定数多項式 H(z) を作成します。

検査官の検査が通るかどうかは誰にもわかりません。難しそうです...

全くない。 Howard Wu の libsnarktutorial に基づいたこの概念実証コードをぜひチェックして、コードに加えられた変更を自分の目で確認してください。

1. C言語ですがビット分解の回路を組むプログラムです。

3. ベリファイアはディスクから Tau をロードし、間違った入力で証明します。検証者は Tau を認識しているため、入力に関係なく定数多項式を生成します。