Introduction: From system architecture to reproducibility assurance

In traditional blockchain systems, proof-of-work relies primarily on the randomness of hashing operations to ensure security. Gonka PoW 2.0, however, faces a more complex challenge: how to ensure unpredictable results for computations based on large language models while ensuring that any honest node can reproduce and verify the same computational process. This article will delve into how MLNode achieves this goal through a carefully designed seeding mechanism and deterministic algorithm.

Before delving into the specific technical implementation, we need to first understand the overall design of the PoW 2.0 system architecture and the key role that reproducibility plays in it.

1. Overview of PoW 2.0 System Architecture

1.1 Layered Architecture Design

Gonka PoW 2.0 adopts a layered architecture to ensure reproducibility from the blockchain level to the computational execution level: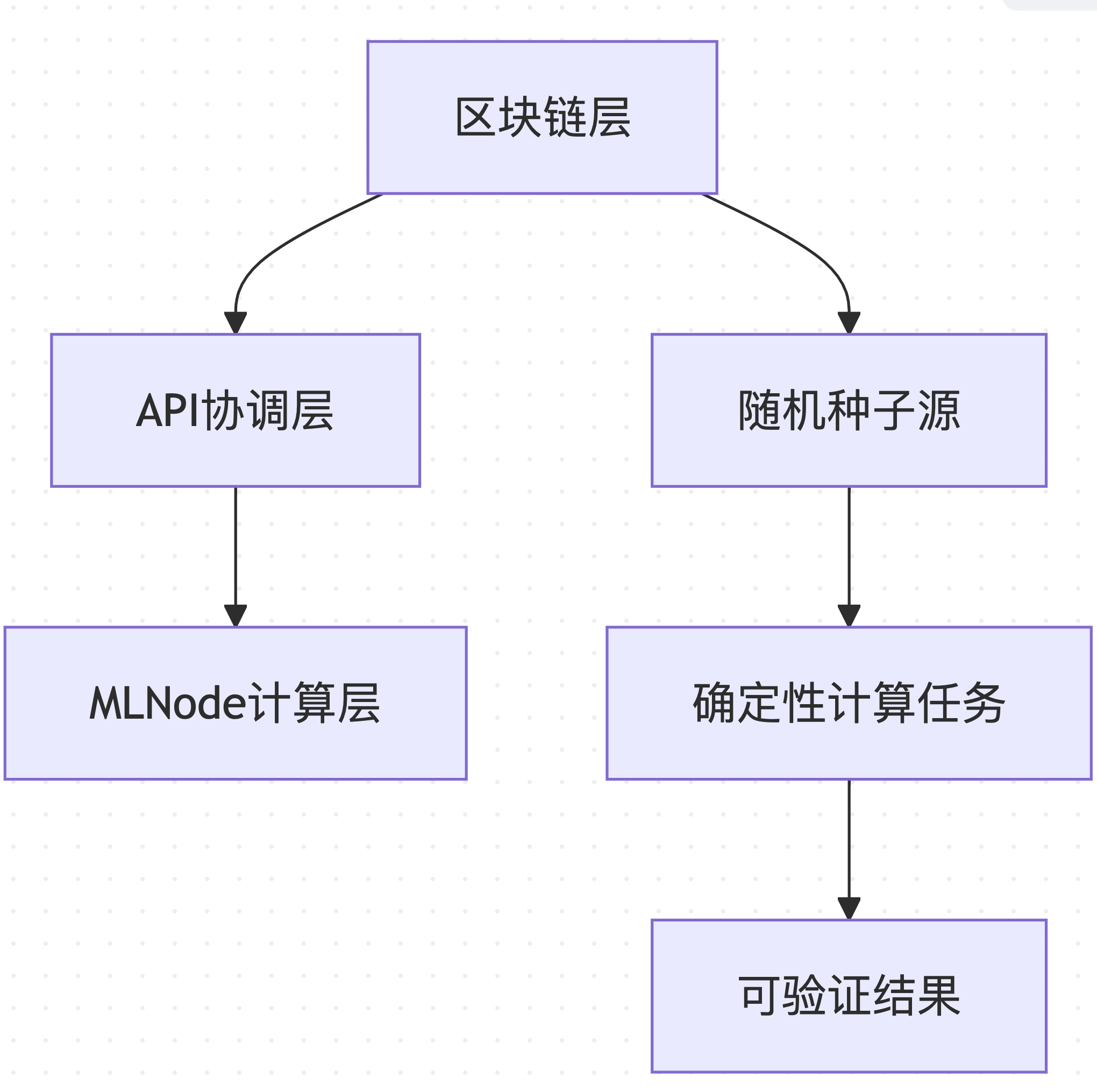

Data source : Based on the architecture design of decentralized-api/internal/poc and mlnode/packages/pow

This layered design allows different components of the system to be optimized independently while maintaining overall consistency and verifiability.

1.2 The core goal of reproducibility

The reproducibility design of PoW 2.0 systems serves the following core goals:

1. Computational fairness : ensuring that all nodes face the same computational challenges

2. Result Verification : Any honest node can reproduce and verify the calculation results

3. Anti-cheating guarantee : making pre-calculation and result falsification computationally infeasible

4. Network synchronization : ensuring state consistency in a distributed environment

Together, these goals form the basis of PoW 2.0’s reproducible design, ensuring the security and fairness of the system.

2. Seed system: unified management of multi-level randomness

After understanding the system architecture, we need to delve into the key technology for achieving reproducibility: the seed system. This system ensures consistency and unpredictability of computations through multi-level randomness management.

2.1 Seed Type and Specific Target

Gonka PoW 2.0 designs four different types of seeds, each serving a specific computational goal:

Network-Level Seeds

Data source : decentralized-api/internal/poc/random_seed.go#L90-L111

Goal : Provide a unified randomness base for the entire network at every epoch, ensuring that all nodes use the same global randomness source.

The network-level seed is the foundation of randomness for the entire system, ensuring that all nodes in the network use the same randomness foundation through blockchain transactions.

Task-Level Seeds

Data source : mlnode/packages/pow/src/pow/random.py#L9-L21

Goal : To produce a high-quality random number generator for every computational task by expanding the entropy space through multiple rounds of SHA-256 hashing.

Task-level seeds provide high-quality randomness for each specific computing task by expanding the entropy space.

Node-Level Seeds

Data source : Seed string construction pattern `f"{hash_str}_{public_key}_nonce{nonce}"`

Goal : Ensure that different nodes and different nonce values produce completely different computation paths to prevent collisions and duplications.

Node-level seeds ensure that the computation path of each node is unique by combining the node public key and the nonce value.

Target Vector Seeds

Data source : mlnode/packages/pow/src/pow/random.py#L165-L177

Goal : Generate a unified target vector for the entire network, where all nodes are optimized towards the same high-dimensional spherical position.

The target vector seed ensures that all nodes in the network calculate towards the same goal, which is the key to verifying the consistency of the results.

2.2 Seed life cycle management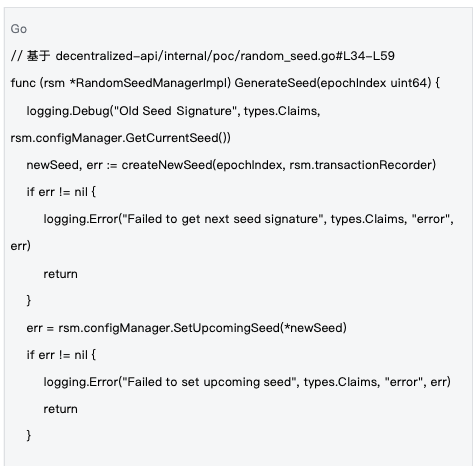

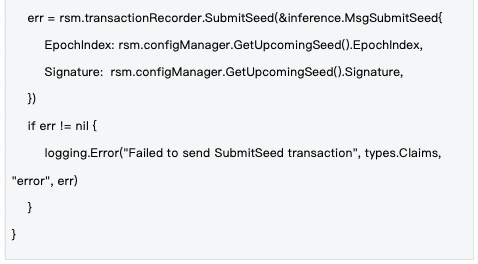
Management mechanism : Seeds are managed at the epoch level. A new seed is generated at the beginning of each epoch and synchronized to the entire network through blockchain transactions to ensure that all nodes use the same randomness base.

The lifecycle management of seeds ensures the timeliness and consistency of randomness, and is an important guarantee for the safe operation of the system.

3. Seed-driven generation mechanism of LLM components

Now that we have a clear understanding of the seed system, we need to explore how to apply these seeds to the generation of LLM components. This is the key to achieving reproducibility.

3.1 Random Initialization of Model Weights

Why do we need to randomly initialize model weights?

In traditional deep learning, model weights are usually obtained through pre-training. However, in PoW 2.0, in order to ensure:

1. Unpredictability of computational tasks : The same input will not produce predictable outputs due to fixed weights

2. ASIC resistance : specialized hardware cannot be optimized for fixed weights

3. Fair competition : All nodes use the same random initialization rules

Data source : mlnode/packages/pow/src/pow/random.py#L71-L88

Randomly initializing model weights is a key step to ensure computational unpredictability and fairness.

Deterministic process for weight initialization

Data source : mlnode/packages/pow/src/pow/compute/model_init.py#L120-L125

Key Features :

• Use block hash as random seed to ensure all nodes generate the same weight

• Use normal distribution N(0, 0.02²) for weight initialization

• Support different data types (such as float16) for memory optimization

This deterministic process ensures that different nodes generate exactly the same model weights under the same conditions.

3.2 Input Vector Generation Mechanism

Why do we need a random input vector?

Traditional PoW uses fixed data (such as a transaction list) as input, but PoW 2.0 needs to generate a different input vector for each nonce to ensure:

1. Continuity of search space : different nonce corresponds to different calculation paths

2. Unpredictable results : small changes in input lead to large differences in output

3. Efficiency of verification : Verifiers can quickly reproduce the same input

Data source : mlnode/packages/pow/src/pow/random.py#L129-L155

The generation of random input vectors ensures the diversity and unpredictability of the computation.

Mathematical basis for input generation

Data source : mlnode/packages/pow/src/pow/random.py#L28-L40

Technical features :

• Each nonce corresponds to a unique seed string

• Generate embedding vectors using standard normal distribution

• Support batch generation to improve efficiency

This mathematical foundation ensures the quality and consistency of the input vectors.

3.3 Output Permutations Generation

Why do we need to output the permutation?

In the output layer of LLM, the vocabulary is usually large (e.g., 32K-100K tokens). To increase computational complexity and prevent targeted optimization, the system randomly permutes the output vectors:

Data source : mlnode/packages/pow/src/pow/random.py#L158-L167

Output permutation increases the complexity of calculation and improves the security of the system.

Application mechanism of arrangement

Data source : Based on the processing logic in mlnode/packages/pow/src/pow/compute/compute.py

Design goals :

• Increase the complexity of the computational challenge

• Prevent optimization of specific vocabulary positions

• Maintaining determinism to support verification

This application mechanism ensures the validity and consistency of the arrangement.

4. Calculation of distance between target vector and sphere

After understanding the generation mechanism of LLM components, we need to further explore the core computational challenge in PoW 2.0 - calculating the distance between the target vector and the sphere.

4.1 What is a target vector?

The target vector is the "bull's eye" of the PoW 2.0 computational challenge - all nodes try to make their model output as close as possible to this predetermined high-dimensional vector.

Mathematical properties of the target vector

Data source : mlnode/packages/pow/src/pow/random.py#L43-L56

Key Features :

• The vector lies on the high-dimensional unit sphere (||target|| = 1)

• Use Marsaglia's method to ensure uniform distribution over the sphere

• All dimensions have equal probability of being selected

The mathematical properties of the target vector ensure fairness and consistency in the computational challenge.

4.2 Why compare results on the sphere?

Mathematical advantage

1. Normalization advantage : All vectors on the sphere have unit length, eliminating the influence of vector magnitude

2. Geometric intuition : Euclidean distance on the sphere directly corresponds to angular distance

3. Numerical stability : avoids computational instability caused by large numerical ranges

Special properties of high-dimensional geometry

In high-dimensional spaces (such as 4096-dimensional vocabulary space), spherical distributions have counterintuitive properties: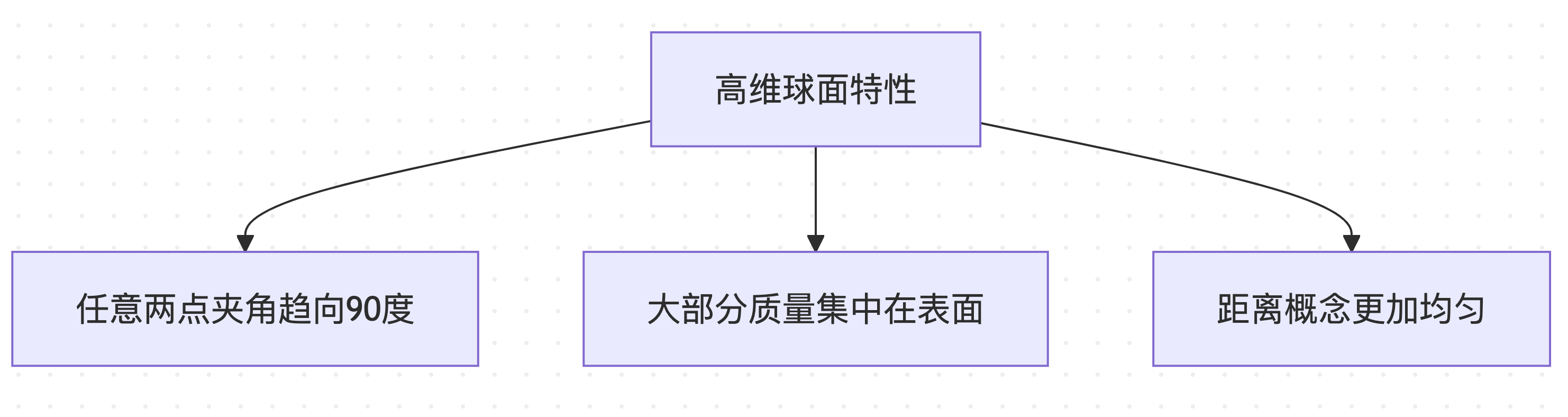

These special properties make spherical distance calculation an ideal computationally challenging metric.

4.3 r_target estimation and PoC stage initialization

The concept and calculation of r_target

r_target is a key difficulty parameter that defines the distance threshold for a "successful" computation result. Results with a distance less than r_target are considered valid proof of work.

Data source : decentralized-api/mlnodeclient/poc.go#L12-L14

In Gonka PoW 2.0, the default value of r_target is set to 1.4013564660458173. This value was determined through extensive experimentation and statistical analysis, aiming to balance computational difficulty and network efficiency. Although there is a dynamic adjustment mechanism in the system, it will be close to this default value in most cases.

r_target initialization in the PoC phase

At the beginning of each PoC (Proof of Computation) phase, the system needs to:

1. Evaluate network computing power : Estimate the total computing power of the current network based on historical data

2. Adjust the difficulty parameter : Set an appropriate `r_target` value to maintain a stable block time

3. Synchronize network-wide parameters : Ensure all nodes use the same `r_target` value

Technical implementation :

• r_target value is synchronized to all nodes through blockchain state

• Each PoC stage may use a different r_target value

• Adaptive adjustment algorithm adjusts difficulty based on the success rate of the previous stage

This initialization mechanism ensures the stable operation and fairness of the network.

5. Engineering assurance of reproducibility

After understanding the core algorithm, we need to focus on how to ensure reproducibility in engineering implementation. This is the key to ensuring the stable operation of the system in actual deployment.

5.1 Deterministic Computing Environment

Data source : Based on the environment settings of mlnode/packages/pow/src/pow/compute/model_init.py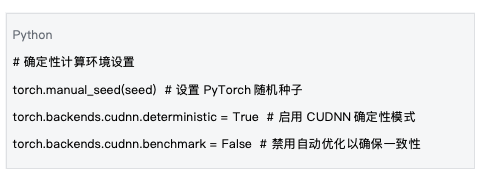

The establishment of a deterministic computing environment is the basis for ensuring reproducibility.

5.2 Numerical Precision Management

Numerical precision management ensures the consistency of calculation results on different hardware platforms.

5.3 Cross-platform compatibility

The system design takes into account the compatibility of different hardware platforms:

- CPU vs GPU : Supports generating the same computational results on both CPU and GPU

-Different GPU models : ensure consistency through standardized numerical precision

- Operating system differences : use standard math libraries and algorithms

Cross-platform compatibility ensures stable operation of the system in various deployment environments.

6. System performance and scalability

On the basis of ensuring reproducibility, the system also needs to have good performance and scalability, which is the key to ensure the efficient operation of the network.

6.1 Parallelization Strategy

Data source : mlnode/packages/pow/src/pow/compute/model_init.py#L26-L53

The parallelization strategy fully utilizes the computational power of modern hardware.

6.2 Memory Optimization

The system optimizes memory usage through various strategies:

- Batch optimization : Automatically adjust batch size to maximize GPU utilization

-Precision selection : Use float16 to reduce memory usage

- Gradient management : disable gradient calculation in inference mode

Memory optimization ensures efficient system operation in resource-constrained environments.

Summary: The engineering value of reproducible design

After an in-depth analysis of the reproducible design of PoW 2.0, we can summarize its technical achievements and engineering value.

Core technology achievements

1. Multi-level seed management : A complete seed system from network level to task level to ensure a balance between determinism and unpredictability in computing

2. Systematic randomization of LLM components : a unified randomization framework for model weights, input vectors, and output permutations

3. Engineering Applications of High-Dimensional Geometry : Designing Fair Computing Challenges Using Spherical Geometric Properties

4. Cross-platform reproducibility : Ensure consistency across different hardware platforms through standardized algorithms and precision control

Together, these technical achievements form the core of PoW 2.0’s reproducible design.

The innovative value of system design

While maintaining blockchain security, Gonka PoW 2.0 successfully shifts computing resources from meaningless hashing operations to valuable AI computations. Its reproducible design not only ensures system fairness and security but also provides a viable technical paradigm for future "meaningful mining" models.

Technical impact :

• Provides a verifiable execution framework for distributed AI computing

• Demonstrated compatibility of complex AI tasks with blockchain consensus

• Established design standards for a new type of proof-of-work

Through a carefully designed seed system and deterministic algorithm, Gonka PoW 2.0 achieves a fundamental shift from traditional "waste-based security" to "value-based security", opening up a new path for the sustainable development of blockchain technology.

Note: This article is based on the actual code implementation of the Gonka project. All code examples and technical descriptions are from the project's official code repository.

About Gonka.ai

Gonka is a decentralized network designed to provide efficient AI computing power. Its design goal is to maximize the use of global GPU computing power to complete meaningful AI workloads. By eliminating centralized gatekeepers, Gonka provides developers and researchers with permissionless access to computing resources while rewarding all participants with its native GNK token.

Gonka was incubated by US AI developer Product Science Inc. Founded by the Libermans siblings, Web 2 industry veterans and former core product directors at Snap Inc., the company successfully raised $18 million in 2023 from investors including OpenAI investor Coatue Management, Solana investor Slow Ventures, K5, Insight, and Benchmark Partners. Early contributors to the project include well-known leaders in the Web 2-Web 3 space, such as 6 Blocks, Hard Yaka, Gcore, and Bitfury.

Official Website | Github | X | Discord | Whitepaper | Economic Model | User Manual