Original author:Vitalik Buterin

Original author:

• The current Data Availability Sampling (DA Sampling or DAS) scheme is done using KZG commitments. The advantage of KZG promises is that they are very easy to use and have some very nice algebraic properties:

• An evaluation proof has constant size and can be verified in constant time.

• Here exists an algorithm to compute all proofs that evaluate deg at each of the N roots of unity in O(N∗log(N)) time

• You can linearly combine commitments to get this linear combination of commitments: com(P)+com(Q)=com(P+Q)

You can linearly combine proofs: Proof(P,x)+Proof(Q,x)+Proof(P+Q,x)

The first point is a good efficiency guarantee. The second point ensures that it is easy to generate blobs ready for DA sampling: if it takes O(N2) this long to generate all proofs, it would require highly centralized actors or complex distributed algorithms to make it DAS-ready.

• The third and fourth points are very valuable for 2D sampling and enable distributed block producers and efficient self-healing:

• Block producers only need to know the original M commitment to use an FFT-over-the-curve to "extend the column" and generate

Not only can you do per-row reconstruction, but you can also do per-column reconstruction: if some values ​​and proofs on a column are missing (but more than half are still available), you can perform an FFT to recover the missing values ​​and proofs.However, KZG has a weakness: it relies on complex pairing cryptography and trusted settings. Pair cryptography has been researched and used for over 20 years, the trusted setup is 1 trust assumption in N, where N is hundreds of participants, so the risk in practice is high, and the authors feel that continuing to use KZG is perfectly acceptable . However, it's worth asking a question:

If we don't want to pay the cost of KZG, can we use inner product parameter (IPA) instead?

See the first half of this article for an explanation of IPA.

• IPA has the following properties:

• Evaluation proves to have logarithmic size and can be verified in linear time (about 40 ms for a polynomial of size 4096)

• There is no known efficient multi-proof generation algorithm.

• Commitments are elliptic curve points, you can combine them linearly like KZG commitments

There is no known method for proofs of linear combinations.

So we keep some properties and lose some. In fact, we've lost enough that our "current method" of generating, distributing, and self-healing proofs is no longer possible. This post describes an alternative method, which is a bit clunky but still achieves the goal.

an alternative

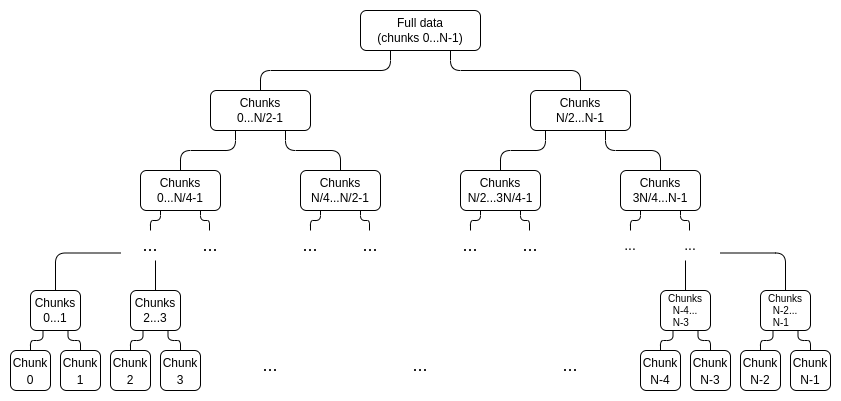
First, we generate a proof tree instead of deg

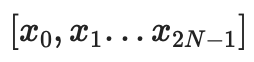
We interpret the data in evaluation form, treating it as a vector:

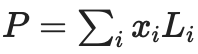
, where the polynomial

(where Li is the deg<2N polynomial equal to 1 at coordinate i and 0 other coordinates in the set).

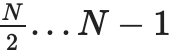
Each node in the proof tree is a commitment to that part of the data, and a proof that this commitment is actually "in bounds". For example,

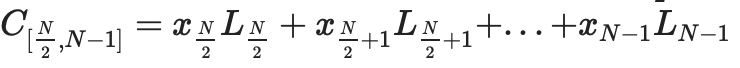
The node will contain the promise

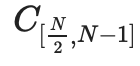
. There will be an IPA certificate,

Actually a linear combination of these points and no other points.

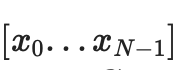
We generate two trees, the first for

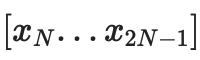
, the second for
, a "complete" commitment to a piece of data consists of C[0,N−1] and C[N,2N−1].

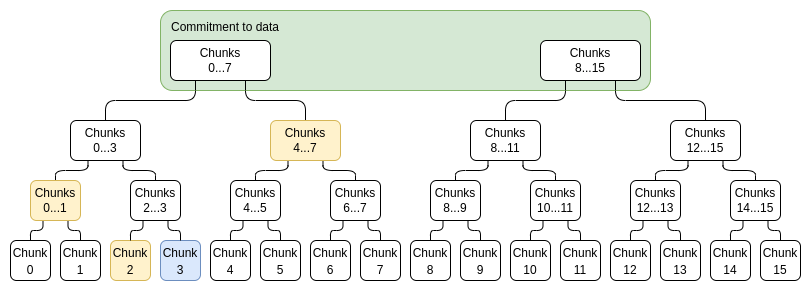
To prove a particular value xi, we simply provide a list of (subcommitment, proof) pairs covering the entire range 0...N−1 or N....2N−1 (whichever contains i), Not including i, and a top-level commit that i doesn't belong to is proof of correct construction. For example, if N=8 and i=3, the proof would contain C[0,1], C2, C[4,7] and their proofs, and a proof that C[8,15] was constructed correctly. The proof will be verified by verifying the individual proofs and checking that the commitments add up to a full commitment.

Blue: chunk 3, yellow: proof of chunk 3.

Note that each chunk need not be a single evaluation for efficiency; instead, we can prune the tree such that a chunk is a set of 16 evaluations. Given that the combined size of the proof will be larger than this anyway, we lose very little by making chunks larger like this.

Generating these proofs takes O(N∗log(N)) time. Verifying a proof takes O(N) time, but note that many proofs can be verified in batches: the O(N) step of verifying an IPA is a linear combination of elliptic curves, many of which we can check using random linear combinations. Each proof still requires O(N) field operations, but this only takes <1 ms.

Expansion: fanout (fanout) is greater than 2

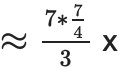
Instead of having 2 fanouts per step, we can have a higher fanout, say 8 fanouts. Instead of one proof per commitment we will have 7 proofs per commitment. For example, at the bottom layer we would have a proof {1,2,3,4,5,6,7}, {0,2,3,4,5,6,7}, {0,1,3,4 ,5,6,7} etc. This increases the total proof generation work by

(7 proofs per node, each proof size is 1.75 times the original size, but 3 times fewer layers, so ~4.08 x more effort), but it reduces the proof size by 3 times.

proof size

Suppose we are dealing with N=128 chunks of size 32 (so we have deg<4096 polynomials) and a fanout of (4x, 4x, 8x). A single branch proof will contain 3 IPAs with a total size of 2∗(7+9+12)=56 curve points (~1792 bytes) plus the chunk's 512 bytes. Today a 256 byte or 512 byte chunk has a 48 byte proof.

Generating the proof requires a total of 2∗8192∗(3∗2+7) curve multiplications (3*2 for two fanout-4 layers, 7 for fanout-8 layers), or ~212992 multiplications in total. So this needs to be done quickly by a powerful computer (a normal computer can do a multiplication in about 50 microseconds, so this takes 10 seconds, which is a bit too long), or a distributed process where different Nodes specialize in different chunks.

Verifying the proof is easy because proofs can be verified in batches and only one elliptic curve multiplication is done. So it shouldn't be much slower than using a KZG proof.

self-healing

Cannot effectively self-heal on a column-by-column basis. But can we avoid requiring a single fix to have all the data (all 2N chunks from all 2M polynomials)?

Assume a single row is completely lost. It is easy to use any column to reconstruct the values ​​in missing rows in that column. But how to prove it?

The simplest technique is cryptoeconomics: anyone can simply issue a bond claiming a value, and then someone can use that claim with branch proofs proving a different value to slash that validator. As long as enough legitimate claims are available, someone on the bank's subnet can put the claims together and reconstruct the commitment and proof. Validators may even be required to issue such claims against the sample indices assigned to them.An alternative that has no cryptoeconomics but is technically more complex and slower is to pass an M-branch proof of the value along that column, along with a proof of correct verification。