書接上回，關於《用多因子模型建立強大的加密資產投資組合》系列文章中，我們已經發布了四篇：《理論基礎篇》、《資料預處理篇》、《因子有效性檢驗篇》、《大類因子分析：因子合成篇》。

在上一篇中，我們具體解釋了因子共線性（因子之間相關性較高）的問題，在進行大類因子合成前，需要進行因子正交化來消除共線性。

一、因子正交化的數學推導

從多因子截面回歸角度，建立因子正交化系統。

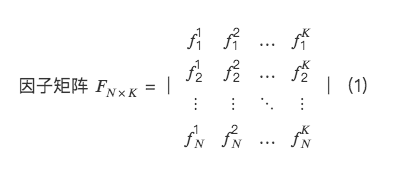
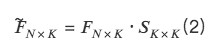
所以，

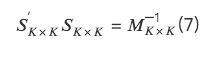
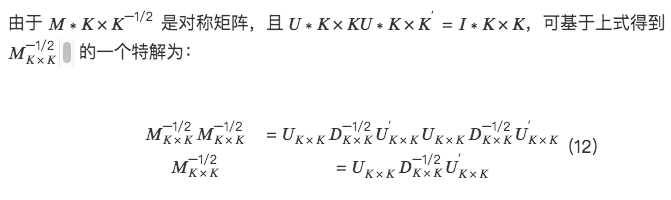
二、三種正交方法的具體實現

1.施密特正交

施密特正交是一種順序正交方法，因此需要確定因子正交的順序，常見的正交順序有固定順序（不同截面上取同樣的正交次序），以及動態順序（在每個截面上依某一規則決定其正交次序）。施密特正交法的優點是以同樣順序正交的因子有明確的對應關係，但是正交順序沒有統一的選擇標準，正交後的表現可能受到正交順序標準和視窗期參數的影響。

2.規範正交

# 規範正交def Canonical(self):
 overlapping_matrix = (time_tag_data.shape[ 1 ] - 1) * np.cov(time_tag_data.astype(float))
# 取得特徵值和特徵向量
 eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix)
# 轉換為np 中的矩陣
 eigenvector = np.mat(eigenvector)
 transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5))))
 orthogonalization = np.dot(time_tag_data.T.values, transition_matrix)
 orthogonalization_df = pd.DataFrame(orthogonalization.T, index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]), columns=time_tag_data.columns)
 self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)

3.對稱正交

施密特正交由於在過去若干個截面上都取同樣的因子正交順序，因此正交後的因子和原始因子有明確的對應關係，而規範正交在每個截面上選取的主成分方向可能不一致，導致正交前後的因子沒有穩定的對應關係。由此可見，正交後組合的效果，很大一部分取決於正交前後因子是否有穩定的對應關係。

對稱正交盡可能的減少原始因子矩陣的修改而得到一組正交基底。這樣能夠最大程度地保持正交後因子和原因子的相似性。並且避免像施密特正交法中偏向正交順序中靠前的因子。

對稱正交的性質：

1. 與施密特正交相比，對稱正交不需要提供正交次序，對每個因子是平等看待的

2. 在所有正交過渡矩陣中，對稱正交後的矩陣和原矩陣的相似性最大，即正交前後矩陣的距離最小。