為什麼說“小表模式”zkEVM更為高效
前言
前言
前言
二級標題
前言
以太坊虛擬機是建立在以太坊區塊鏈上的代碼運行環境,合約代碼可對外完全隔離並在EVM 內部運行,其主要作用是處理以太坊系統內的智能合約。之所以說以太坊是圖靈完備,是因為開發者可以使用Solidity 語言創建運行於EVM 上的應用程序,一切可計算的問題都能計算。但僅是圖靈完備還不夠,人們還試圖將EVM 封裝在ZK 證明系統裡,但問題是封裝時會產生大量冗餘。 Fox 所發明的“小表模式”zkEVM,在保證原生的Solidity 以太坊開發者能無縫遷移至zkEVM 的同時,還將大幅削減封裝EVM 到ZK 證明系統時產生的冗餘成本。
第二個方向就是所謂的zkEVM 賽道,該賽道項目致力於EVM Bytecode 的兼容,即Bytecode 級別及其以上的EVM 代碼都通過ZkEVM 產生對應的零知識證明,這樣以來原生的Solidity 以太坊開發者會可以無成本遷移至zkEVM。該賽道選手主要有Polygon zkEVM、Scroll、Taiko 和Fox。該賽道的難點在於兼容EVM 這樣一個並不適合封裝在ZK 證明系統時產生的冗餘成本。 Fox 經歷長時間的思考與論證,終於找到了從根本上消減第一代zkEVM 巨大冗餘的那把鑰匙:“小表模式”zkEVM。
圖片描述

數據和證明電路是zkEVM 生成證明的兩大核心要素。一方面,在zkEVM 中,證明者需要所有交易涉及的數據以證明交易帶來的狀態轉移是正確的,而EVM 中的數據量大且結構複雜。因此,如何整理和組織證明所需的數據便是構建一個高效的zkEVM 需要仔細考慮的問題。另一方面,怎麼通過一系列的電路約束高效地證明(或檢驗)計算執行的有效性與正確性,則是保證zkEVM 安全性的基礎。
圖片描述
圖片描述
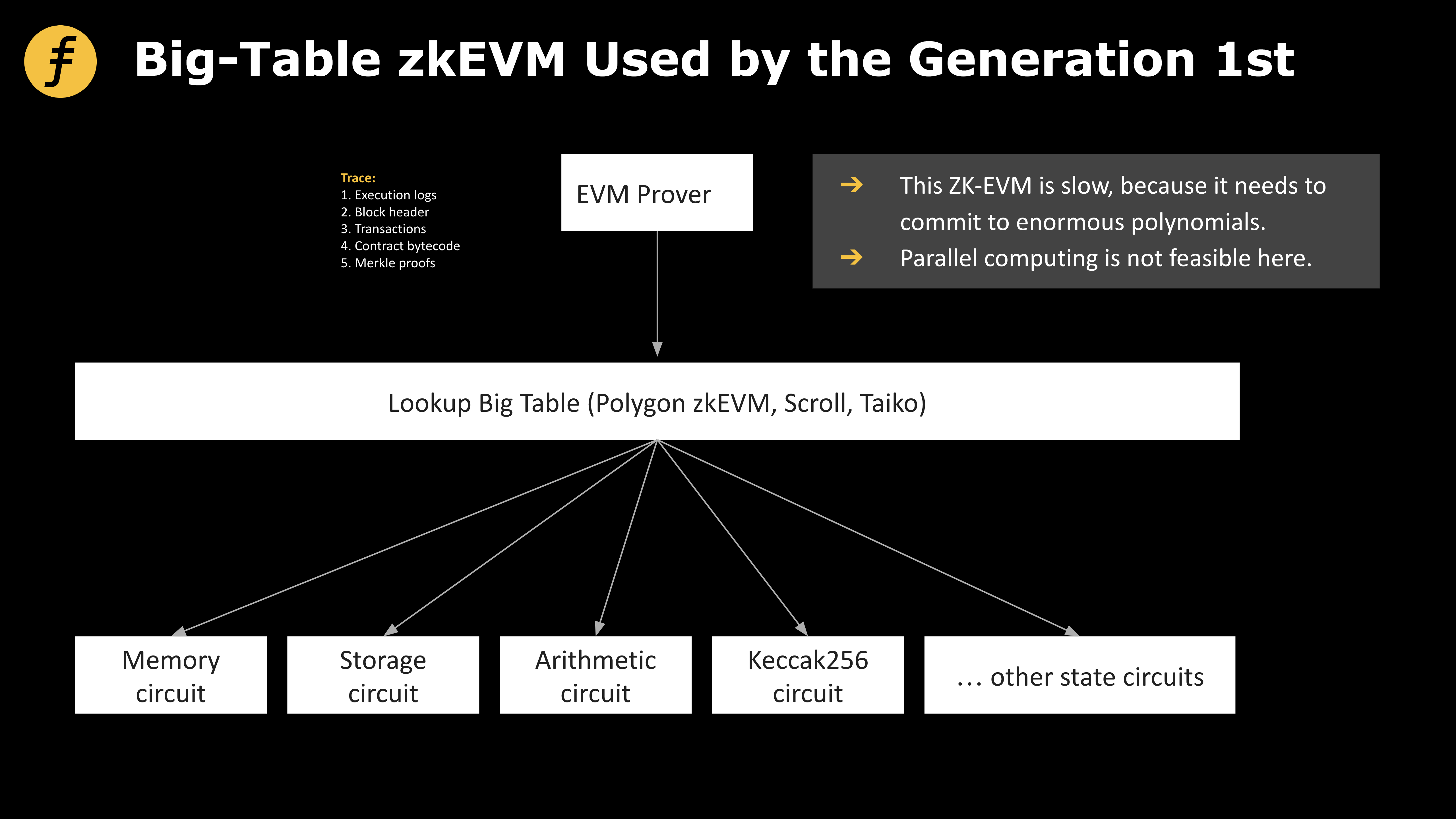
圖1:大表、小表兩代zkEVM 解決方案
例如,我們將每次stack 中元素的變化都放在一塊,專門編寫一個stack 電路證明,為單純的算術操作專門編寫一套的算術電路等等。如此一來,每個電路需要考慮的情況就變得相對簡單。這些不同功能的電路在不同zkEVM 中有不同的名字,有人直接稱其為電路,也有人稱其為(子)狀態機,但是這個思想的本質都是一樣的。
為了更清楚的解釋這麼做的意義,我們舉一個例子,假設現在要證明加法操作(將stack 的上2 個元素取出來,並將他們的和放回stack 頂端):
假設原先的stack 是[ 1, 3, 5, 4, 2 ]
則如果不分類拆分的話,我們需要設法證明進行完上述操作後stack 變為[ 1, 3, 5, 6 ]
而如果進行了分類拆分的話我們只需要分別證明以下幾件事:
stack 電路:
C 3 :a= 2, b= 4,算術電路:
圖片描述
c= 6 ,證明a+b=c
圖片描述
圖片描述
圖2: 第一代zkEVM 採用的大表模式
而一旦分類拆分了,每一個部分的情況將會變得相對單純,從而證明的難度也會顯著減小。
但是分類拆分也會帶來其他問題,那便是不同類別電路的數據一致性問題,例如在上面的例子裡,我們實際上還需要證明以下兩件事:
C 4 :”C 1 中pop 出來的數” = “C 3 中的a 和b”
C 5 :“C 2 中push 的數” = “C 3 中的c”
為了解決這個問題,我們回到了第一個問題,即我們要如何組織交易涉及的數據,下面我們接著探討這個議題:
一個直觀的方法是這樣的:通過trace,我們可以拆解出所有交易涉及的每個步驟,知道其涉及的數據,並通過向節點發送請求以獲得不在trace 中的那部分數據,隨後,我們將其如下排列成一個大表格T:
“第一步操作” “第一步操作涉及的數據”
“第二步操作” “第二步操作涉及的數據”
…“第n 步操作” “第n 步操作涉及的數據”
如此一來,在上面的例子中,我們就會有一行記錄著
C 4(a):C 1 pop 出的數和大表T 中的第k 步一致
圖片描述
C 4(a):C 3 的a 和b 和大表T 中的第k 步一致
圖片描述
圖片描述
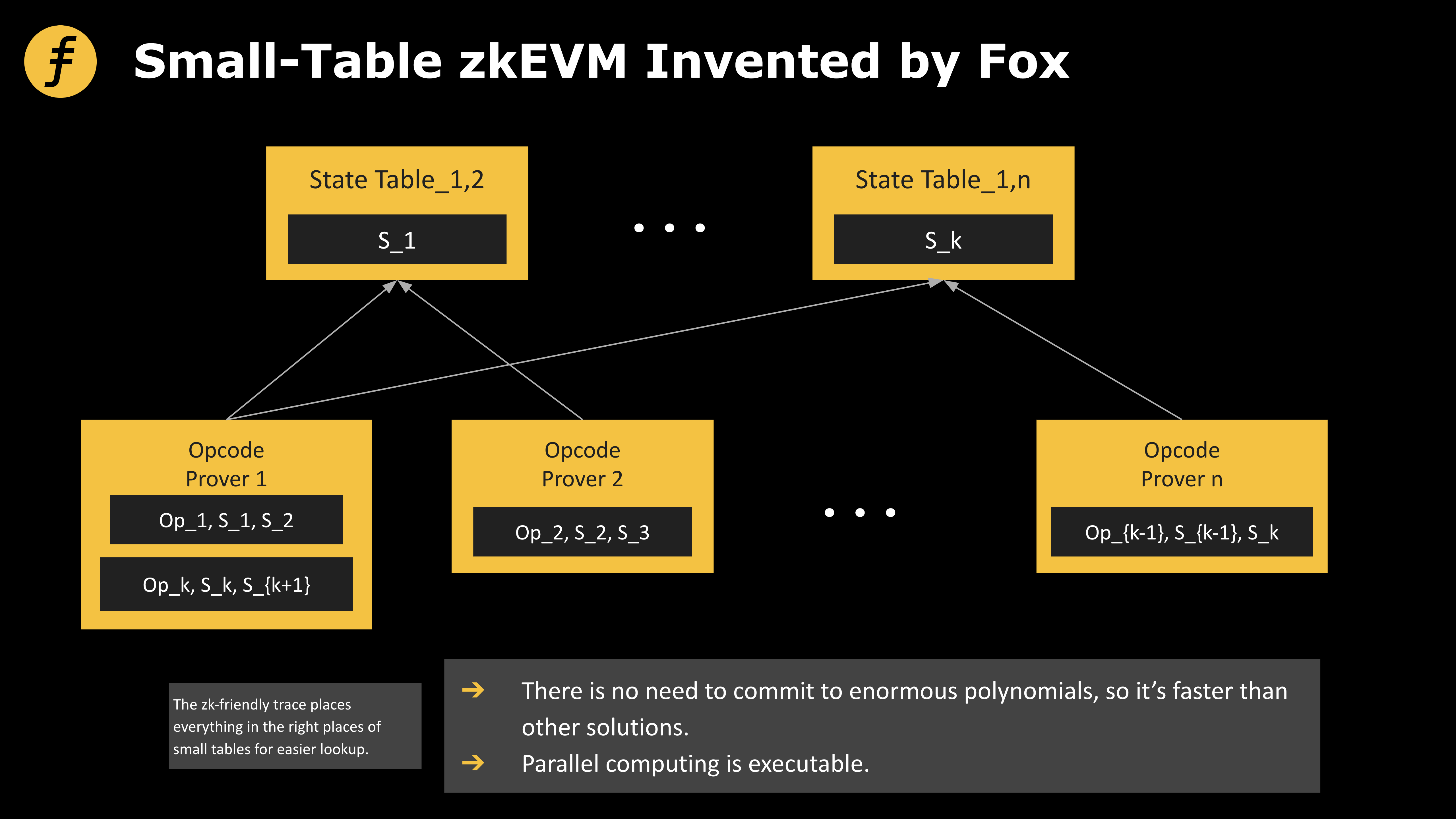
圖3: Fox 所發明的“小表模式”zkEVM
我們考慮如下一系列的表格構造:
表格Ta:
“類型a 的第一個操作” “類型a 的第一個操作涉及的數據”
“類型a 的第二個操作” “類型a 的第二個操作涉及的數據”
…“類型a 的第m 個操作” “類型a 的第m 個操作涉及的數據”
表格Tb:
“類型b 的第一個操作” “類型b 的第一個操作涉及的數據”
一個簡單的例子(假設我們每次只能lookup 一個元素)是如果我們要證明a~h 這8 個字母都存在[a, b, c, d, e, f, g, h]中,我們需要對大小為8 的表進行8 次的lookup,但是如果我們把表分為[a, b, c, d]和[e, f, g, h]的話,我們只需要對這兩個大小為4的表分別進行4 次lookup 就可以了!
結論
結論
結論



