原文作者：Fox Tech CEO 康水躍，Fox Tech 首席科學家孟鉉濟
原文作者：Fox Tech CEO 康水躍，Fox Tech 首席科學家孟鉉濟
原文作者：Fox Tech CEO 康水躍，Fox Tech 首席科學家孟鉉濟
原文作者：Fox Tech CEO 康水躍，Fox Tech 首席科學家孟鉉濟
一級標題
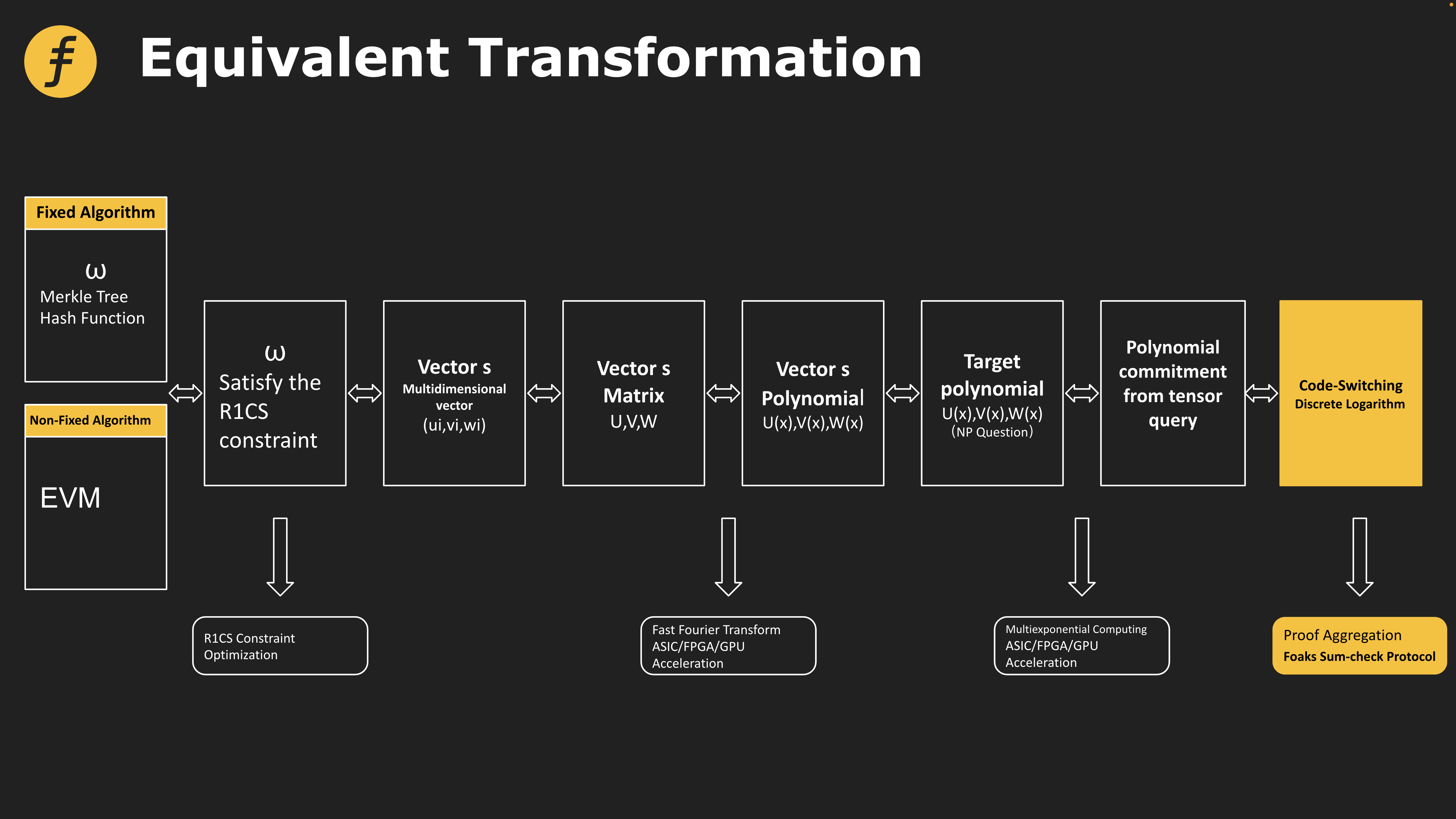
一級標題
Sum-check Protocol
二級標題
二級標題
二級標題
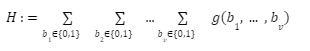
和在zkRollup 當中考慮的“外包計算”的場景類似，在應用當中，上述式子的計算量會非常大，我們希望將這個式子的計算交給證明者（Prover），之後證明者向驗證者（Verifier）證明自己的計算結果是正確的。
二級標題
二級標題
二級標題
第二點，關於協議的目標，事實上sum-check 協議可以對於任意的集合B 計算bBmg(b)，但是不失一般性的，我們假設B={ 0, 1 }。
二級標題
二級標題
二級標題
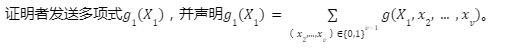
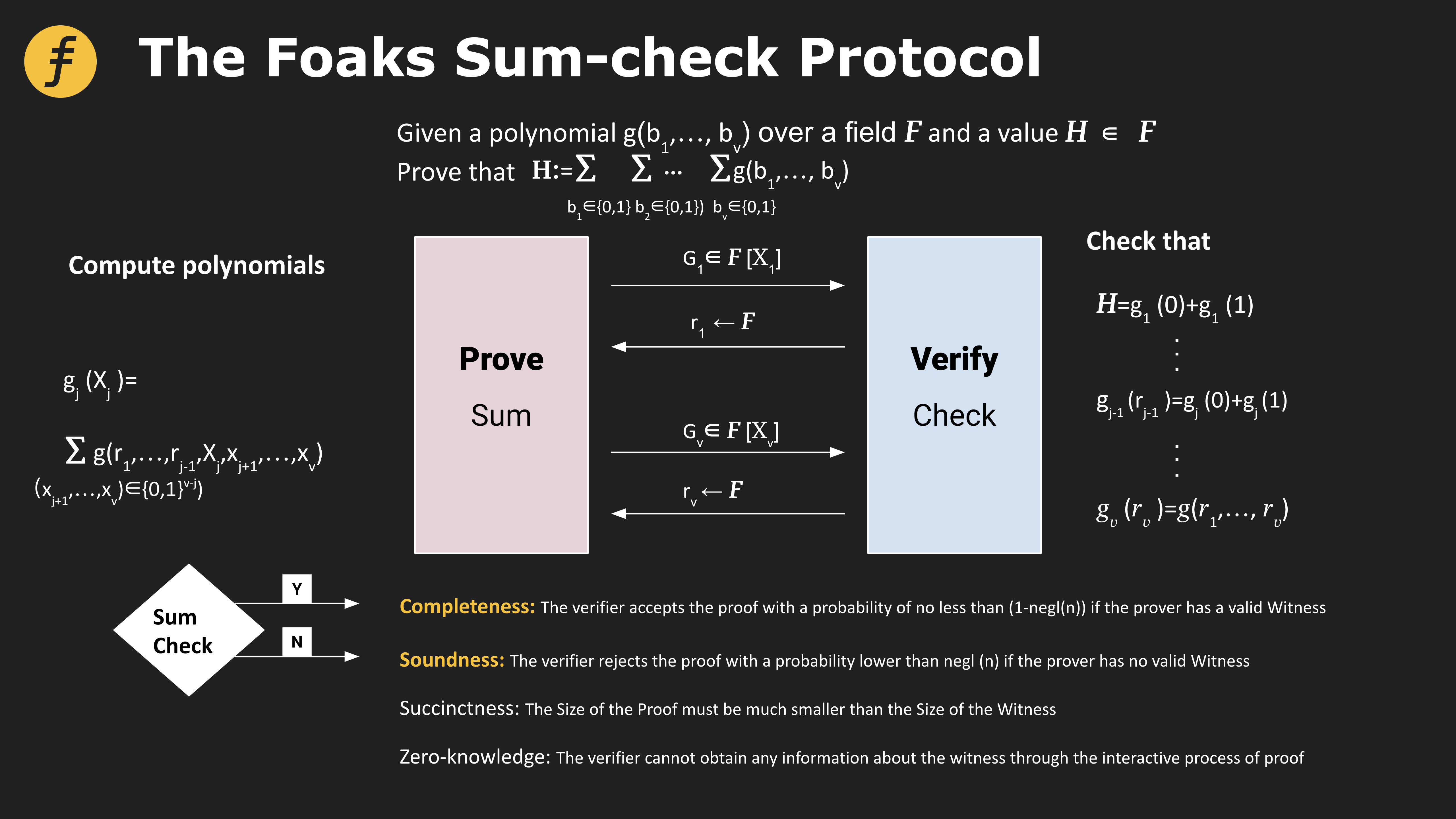
3. 協議過程
協議一共包含v 輪。在每一輪當中會處理g 中的一個變量。
第1 輪：
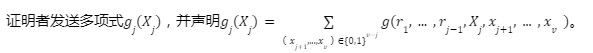
如果證明者是誠實的，應當成立H=g 1( 0)+g 1( 1)。驗證者驗證，若通過則選擇隨機數r 1 發送給證明者。注意到，根據協議的假設，證明者可以完成上述驗證。
第v 輪：
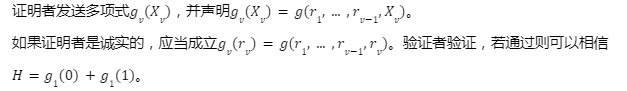
圖片描述
圖片描述
圖片描述
圖2: The Foaks Sum-check protocol
Completeness: 若證明者擁有有效的Witness，則驗證者會以不低於（1-negl(n)）的概率接受證明；
#其中negl（n）為任意可忽略的函數
二級標題
二級標題
4. 協議複雜度
圖3:Sum-check 協議的複雜度
一級標題
一級標題
一級標題
Sum-check Protocol 的應用
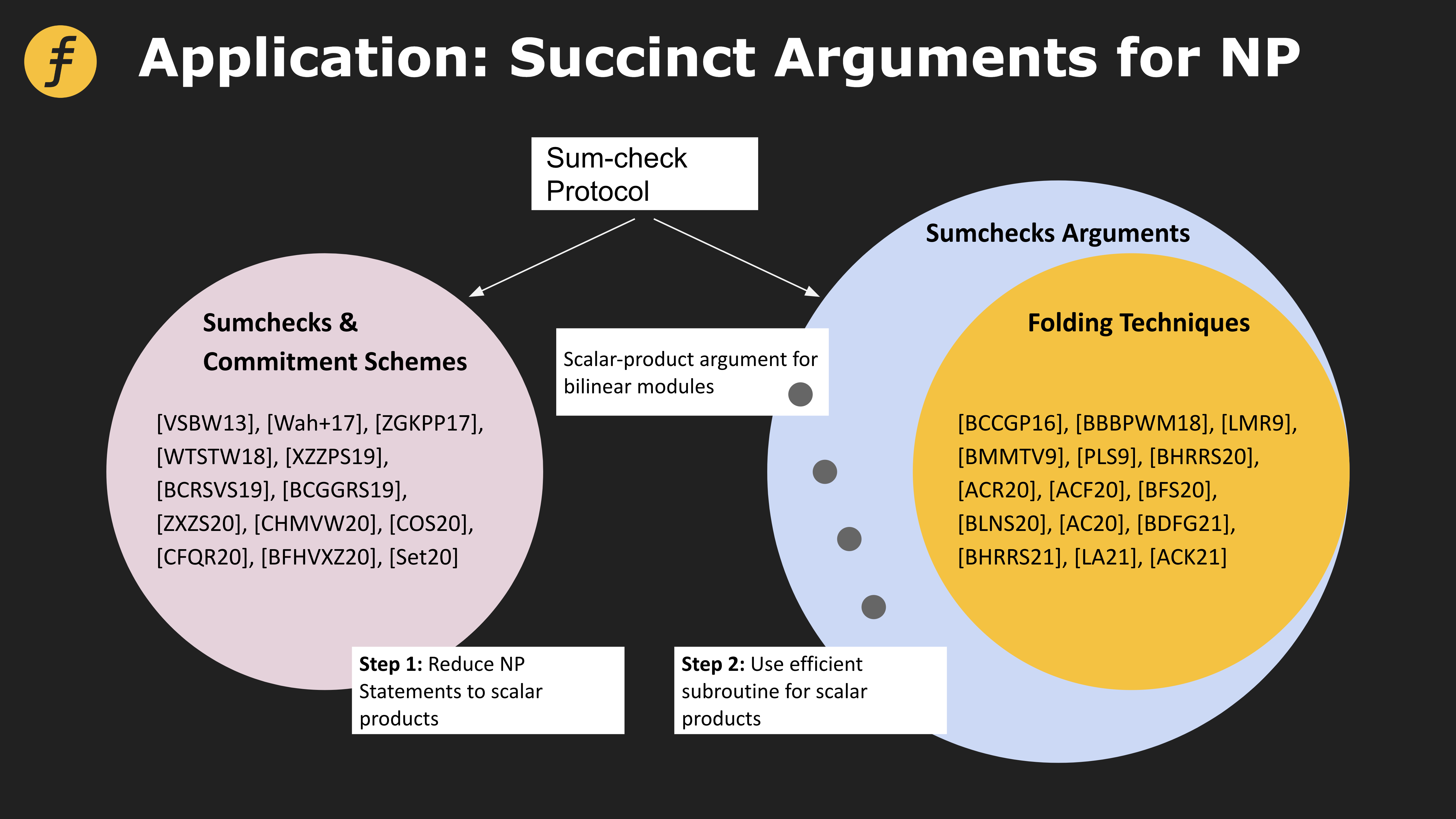
在許多的零知識證明算法當中，sum-check protocol 都在發揮著重要的作用。許多問題的證明，都依賴於將原始的問題轉化為sum-check 的形式，再完成後續的步驟。
首先，我們使用鄰接矩陣A 表示無向圖G，設E 為其邊集合，則Ai, j= 1(i, j)E，也就是說若點i, j 之間存在一條邊則Ai, j = 1 否則為0 。對於點i, j, k，三點構成三角形的條件是Ai, j= 1, Ai, k= 1, Aj, k= 1 。
一級標題
一級標題
結語
結語
一級標題
參考文獻
[LFKN 92 ] Carsten Lund, Lance Fortnow, Howard Karloff, and Noam Nisan. Algebraic methods for interactive proof systems. J. ACM, 39: 859 – 868, October 1992.
https://people.cs.georgetown.edu/jthaler/sumcheck.pdf
參考文獻https://blog.csdn.net/mutourend/article/details/111610754
IOS
Android