深度剖析下個萬億賽道:零知識證明和分佈式計算結合
二級標題
二級標題
二級標題
1.1 發展歷史
最開始的計算機每台只能執行一個計算任務,隨著多核心多線程的CPU 出現,單個計算機可以執行多個計算任務。
隨著大型網站的業務增加,單服務器模式很難進行擴容,又增加硬件成本。面向服務的架構出現,由多台服務器組成。由服務註冊者、服務提供者和服務消費者,三者組成。
但是隨著業務增加和服務器增加,SOA 模式下,點對點服務可維護性和可拓展性難度增加。類似微機原理中,總線模式出現,來協調各個服務單元。服務總線通過類似集線器的架構將所有系統連接在一起。這個組件被稱為ESB(企業服務總線)。作為一個中間角色,來翻譯協調各個不同格式或者標準的服務協議。
隨後基於應用程序編程接口(API)的REST 模型通信,以其簡潔、可組合性更高的特性,脫穎而出。各個服務以REST 形式對外輸出接口。當客戶端通過RESTful API 提出請求時,它會將資源狀態表述傳遞給請求者或終端。該信息或表述通過HTTP 以下列某種格式傳輸:JSON(Javascript 對象表示法)、HTML、XLT、Python、PHP 或純文本。 JSON 是最常用的編程語言,儘管它的名字英文原意為“JavaScript 對象表示法”,但它適用於各種語言,並且人和機器都能讀。GFS: The Google File System
虛擬機、容器技術,以及谷歌的三篇論文:MapReduce: Simplified Data Processing on Large Clusters
2003 年,Bigtable: A Distributed Storage System for Structured Data
2004 年,
2006 年,
二級標題
二級標題
二級標題
正文
正文
正文
1.2.1 為什麼去中心化計算很重要?
正文
正文
正文
1.2.2 整體市場規模有多大?
如何估算市場規模呢?通過Web2領域的分佈式計算業務規模來估算?乘上web3市場的滲透率?把目前市面上相應融資項目的估值相加嗎?
我們不能將Web2的分佈式計算市場規模照搬到Web3,理由是: 1 ,Web2領域的分佈式計算滿足了大部分需求,Web3領域的去中心化計算是差異化滿足市場需求。如果照搬,是有悖於市場客觀背景環境。 2 ,Web3領域的去中心化計算,未來成長出的市場業務範圍是全球化的。所以我們需要更加嚴謹得去估算市場規模。
正文
正文
正文
1.2.3 現在處於什麼階段,未來還有多少空間?
2017 年到現在,很多團隊都在嘗試去中心化計算方向上發展,但是都嘗試失敗,後面會具體解釋失敗的原因。探索路徑由最初類似外星人探索計劃的項目,後來發展到模仿傳統雲計算的模式,再到Web3原生模式的探索。
當前整個賽道的現狀,處於在學術層面已經驗證0 到1 的突破,一些大型項目在工程實踐上,有了較大的進展。例如當前的zkRollup 和zkEVM 實現上,都是剛剛發布產品的階段。
當然這只是提出的一個應用場景,而Web2有很多業務場景需要計算的能力。
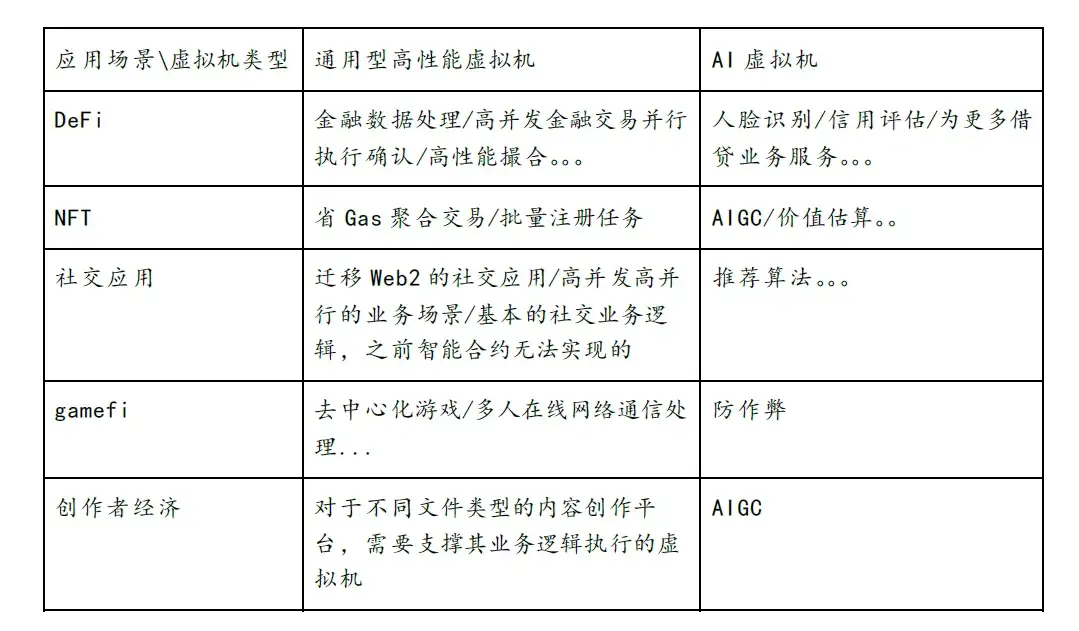
1.2.4 哪些機會值得關注?怎麼去賺錢?
二級標題
二級標題
二級標題
2.1 雲服務模式
目前以太坊有如下問題 :
整體吞吐量低。消耗了大量的算力,但是吞吐量只相當於一台智能手機。
驗證積極性低。這個問題被稱為Verifier's Dilemma。獲得打包權的節點得到獎勵,其他節點都需要驗證,但是得不到獎勵,驗證積極性低。久而久之,可能導致計算得不到驗證,給鏈上數據安全性帶來風險。
計算量受限(gasLimit),計算成本較高。
二級標題
二級標題
二級標題
https://www.aicoin.com/article/256862.html
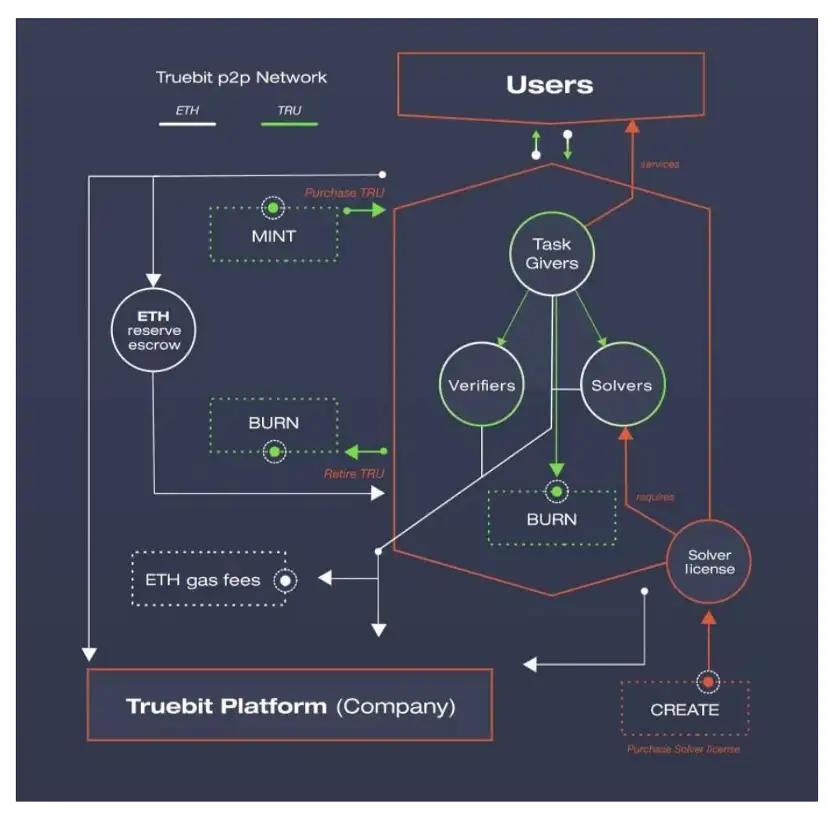
2.2 挑戰者模式
而TrueBit 則利用博弈體系,達到全局最優解,來保障下發的計算任務是被正確執行。
我們快速這種計算框架的核心要點:
角色:問題解決者、挑戰者和法官
問題解決者需要質押資金,才可以參與領取計算任務
挑戰者作為賞金獵人,需要重複驗證問題解決者的計算結果,和自己本地的是否一致
挑戰者會去抽取與兩者計算狀態一致的最近時間的計算任務,如果出現分歧點,提交分歧點的默克樹hash 值
二級標題
二級標題
二級標題
2.3 利用零知識證明驗證計算
所以如何實現,既保證計算過程可被驗證,又能保障驗證的及時性。
在假定條件下,有足夠高性能的零知識證明加速硬件和足夠被優化的零知識證明算法,通用計算場景可以得到充分發展。大量Web2場景下的計算業務,都可以被零知識證明通用虛擬機進行複現。就如前文所提到可賺錢的業務方向。
二級標題
二級標題
二級標題
3.1 學術層面
我們回看一下零知識證明算法歷史發展演進的路線:
GMR 85 是最早起源的算法,來源於Goldwasser、Micali 和Rackoff 合作發表的論文:The Knowledge Complexity of Interactive Proof Systems(即GMR 85 ),該論文提出於1985 年,發表於1989 年。這篇論文主要闡釋的是在一個交互系統中,經過K 輪交互,需要多少知識被交換,從而證明一個證言(statement)是正確的。
姚氏混淆電路(Yao's Garbled Circuit,GC)[ 89 ]。一種著名的基於不經意傳輸的兩方安全計算協議,它能夠對任何函數進行求值。混淆電路的中心思想是將計算電路(我們能用與電路、或電路、非電路來執行任何算術操作)分解為產生階段和求值階段。每一方都負責一個階段,而在每一階段中電路都被加密處理,所以任何一方都不能從其他方獲取信息,但他們仍然可以根據電路獲取結果。混淆電路由一個不經意傳輸協議和一個分組密碼組成。電路的複雜度至少是隨著輸入內容的增大而線性增長的。在混淆電路發表後,Goldreich-Micali-Wigderson(GMW)[ 91 ]將混淆電路擴展使用於多方,用以抵抗惡意的敵手。
sigma 協議又稱為誠實驗證者的(特殊)零知識證明。即假設驗證者是誠實的。這個例子類似Schnorr 身份認證協議,只是後者通常採用非交互的方式。
2013 年的Pinocchio (PGHR 13):Pinocchio: Nearly Practical Verifiable Computation,將證明和驗證時間壓縮到適用範圍,也是Zcash 使用的基礎協議。
2016 年的Groth 16 :On the Size of Pairing-based Non-interactive Arguments,精簡了證明的大小,並提升了驗證效率,是目前應用最多的ZK 基礎算法。
2017 年的Bulletproofs (BBBPWM 17) Bulletproofs: Short Proofs for Confidential Transactions and More,提出了Bulletproof 算法,非常短的非交互式零知識證明,不需要可信的設置, 6 個月以後應用於Monero,是非常快的理論到應用的結合。
2018 年的zk-STARKs (BBHR 18) Scalable, transparent, and post-quantum secure computational integrity,提出了不需要可信設置的ZK-STARK 算法協議,這也是目前ZK 發展另一個讓人矚目的方向,也以此為基礎誕生了StarkWare 這個最重量級的ZK 項目。
Bulletproofs 的特點為:
1 )無需trusted setup 的short NIZK
2 )基於Pedersen commitment 構建
3 )支持proof aggregation
4 )Prover time 為:O ( N ⋅ log ( N ) ) O(N\cdot \log(N))O(N⋅log(N)),約30 秒
5 )Verifier time 為:O ( N ) O(N)O(N),約1 秒
6 )proof size 為:O ( log ( N ) ) O(\log(N))O(log(N)),約1.3 KB
7 )基於的安全假設為:discrete log
2 )inner product proofs
Bulletproofs 適用的場景為:
4 )aggregated and distributed (with many private inputs) proofs
1 )range proofs(僅需約600 字節)
3 )MPC 協議中的intermediary checks
Halo 2 主要特點為:
1 )無需trusted setup,將accumulation scheme 與PLONKish arithmetization 高效結合。
2 )基於IPA commitment scheme。\log N)O(N∗logN)。
3 )繁榮的開發者生態。
4 )Prover time 為:O ( N ∗ log N ) O(N*\log N)O(logN)。
5 )Verifier time 為:O ( 1 ) > O( 1)>O( 1)>Groth 16 。
6 )Proof size 為:O ( log N ) O(
7 )基於的安全假設為:discrete log。
Halo 2 適於的場景有:
1 )任意可驗證計算
2 )遞歸proof composition
3 )基於lookup-based Sinsemilla function 的circuit-optimized hashing
Halo 2 不適於的場景為:
1 )除非替換使用KZG 版本的Halo 2 ,否則在以太坊上驗證開銷大。
Plonky 2 主要特點為:
1 )無需trusted setup,將FRI 與PLONK 結合。\log N)O(logN)。
2 )針對具有SIMD 的處理器進行了優化,並採用了64 byte Goldilocks fields。\log N)O(logN)。
3 )Prover time 為:O ( log N ) O(\log N)O(N∗logN)。
4 )Verifier time 為:O ( log N ) O(
5 )Proof size 為:O ( N ∗ log N ) O(N*
6 )基於的安全假設為:collision-resistant hash function。
Plonky 2 適於的場景有:
1 )任意可驗證計算。
2 )遞歸proof composition。
3 )使用自定義gate 進行電路優化。
二級標題
二級標題
二級標題
3.2 工程實踐層面
既然零知識證明在學術層面突飛猛進,具體落地到實際開發時候,目前進展是怎樣的呢?
我們從多個層面去觀察:
編程語言:目前有專門的編程語言,幫助開發者不需要深入了解電路代碼如何設計,這樣就可以降低開發門檻。當然也有支持將Solidity 轉譯成電路代碼。開發者友好程度越來越高。
虛擬機:目前有多種實現的zkvm,第一種是自行設計的編程語言,通過自己的編譯器編譯成電路代碼,最後生成zkproof。第二種是支持solidity 編程語言,通過LLVM 編譯成目標字節碼,最後轉譯成電路代碼和zkproof。第三種是真正意義的EVM 等效兼容,最終將字節碼的執行操作,轉譯成電路代碼和zkproof。目前是zkvm 的終局之戰嗎?並沒有,不管是拓展到智能合約編程之外的通用計算場景,還是不同方案的zkvm 針對自身底層指令集的補齊和優化,都還是1 到N 的階段。任重而道遠,大量工程上的工作需要去優化和實現。各家在學術層到工程實現上實現了落地,誰能最終成為王者,殺出一條血路。不僅需要在性能提升有大幅進展,還要能吸引大量開發者進入生態。時間點是十分重要的前提要素,先行推向市場,吸引資金沉澱,生態內自發湧現的應用,都是成功的要素。
週邊配套工具設施:編輯器插件支持、單元測試插件、Debug 調試工具等等,幫助開發者更加高效的開發零知識證明應用。
明星項目湧現:zkSync、Starkware 等等優質項目,相繼宣布其正式產品發布的時間。說明了,零知識證明和去中心化計算結合不再是停留在理論層面,在工程實踐上逐漸成熟。
二級標題
二級標題
二級標題
4.1 zkProof 生成效率低
前面我們講到,關於這塊市場容量、目前行業發展情況、在技術上的實際進展,但是沒有存在一點挑戰嗎?
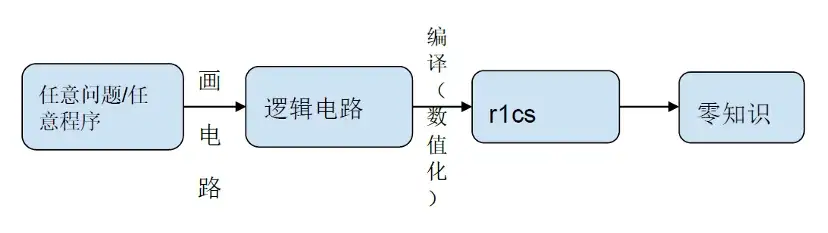
我們對整個zkProof 生成的流程進行拆解:
在邏輯電路編譯數值化r 1 cs 的階段,裡面80% 的運算量在NTT 和MSM 等計算業務上。另外對邏輯電路不同層級進行hash 算法,隨著層級越多,Hash 算法時間開銷線性增加。當然現在行業內提出時間開銷減少200 倍的GKR 算法。
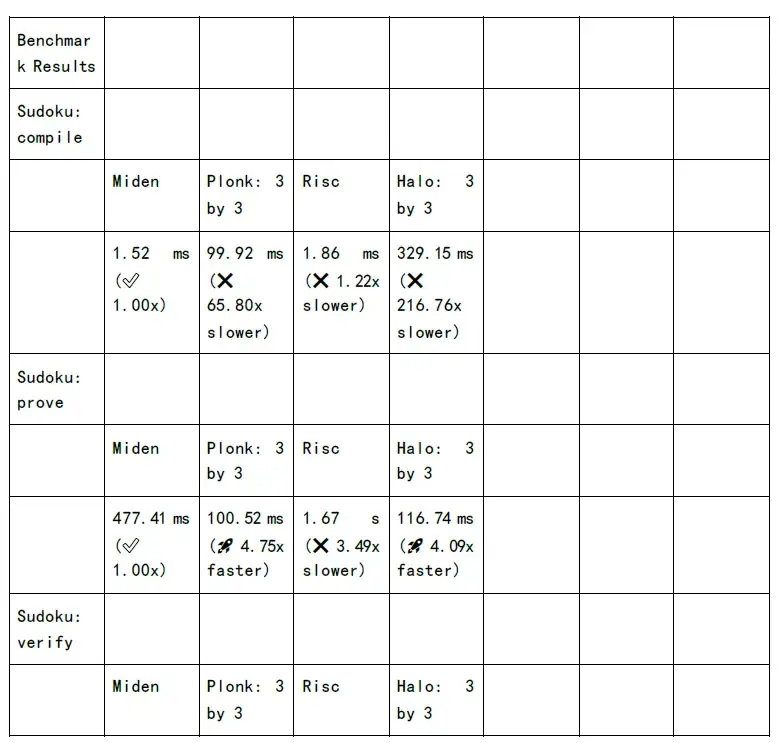
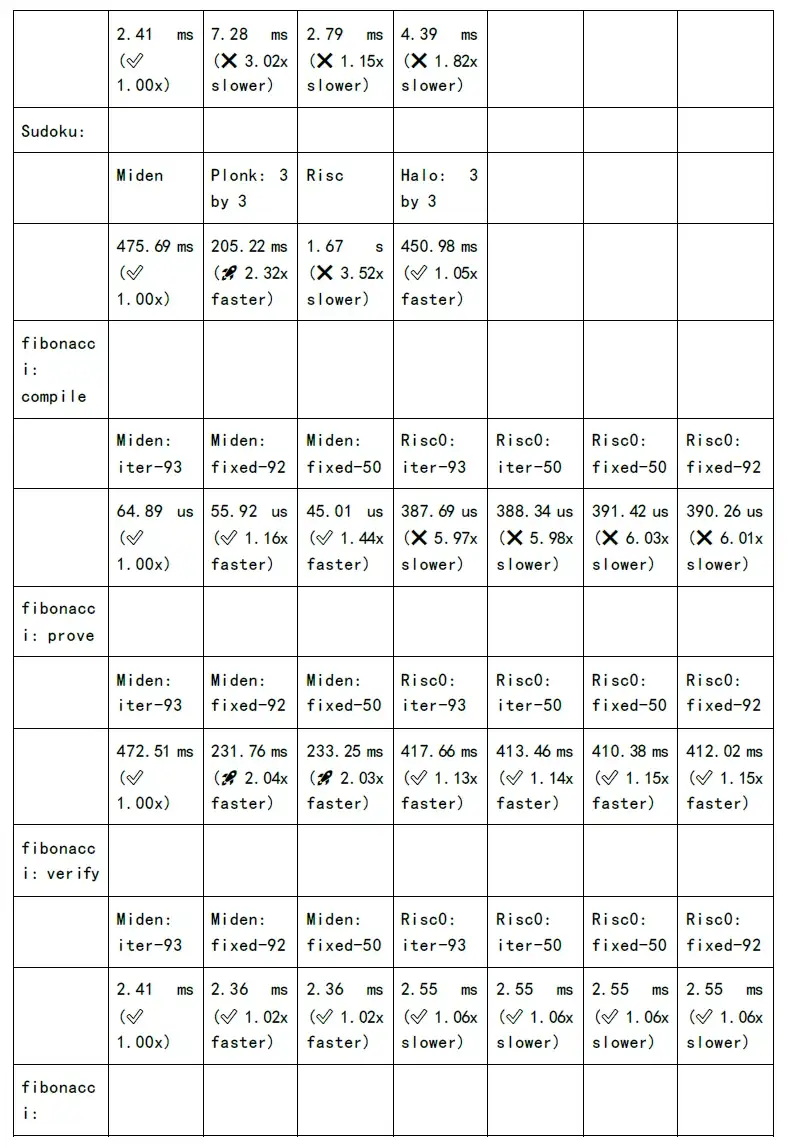
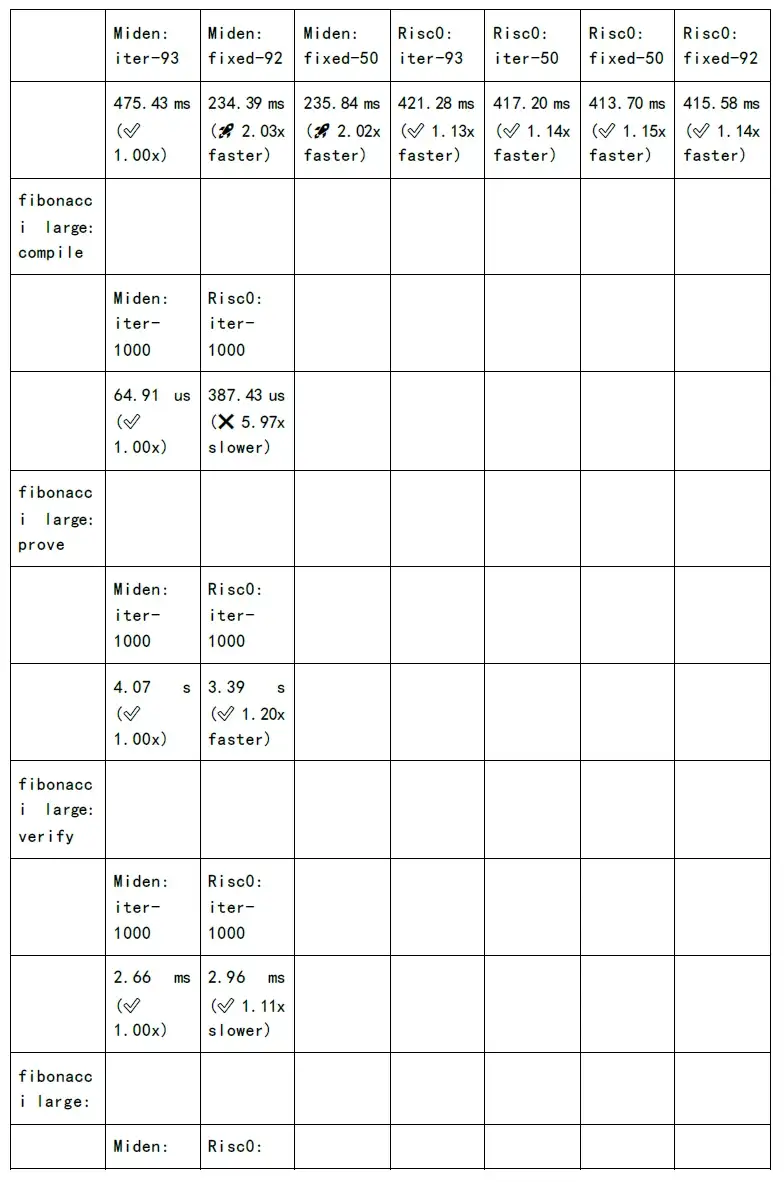
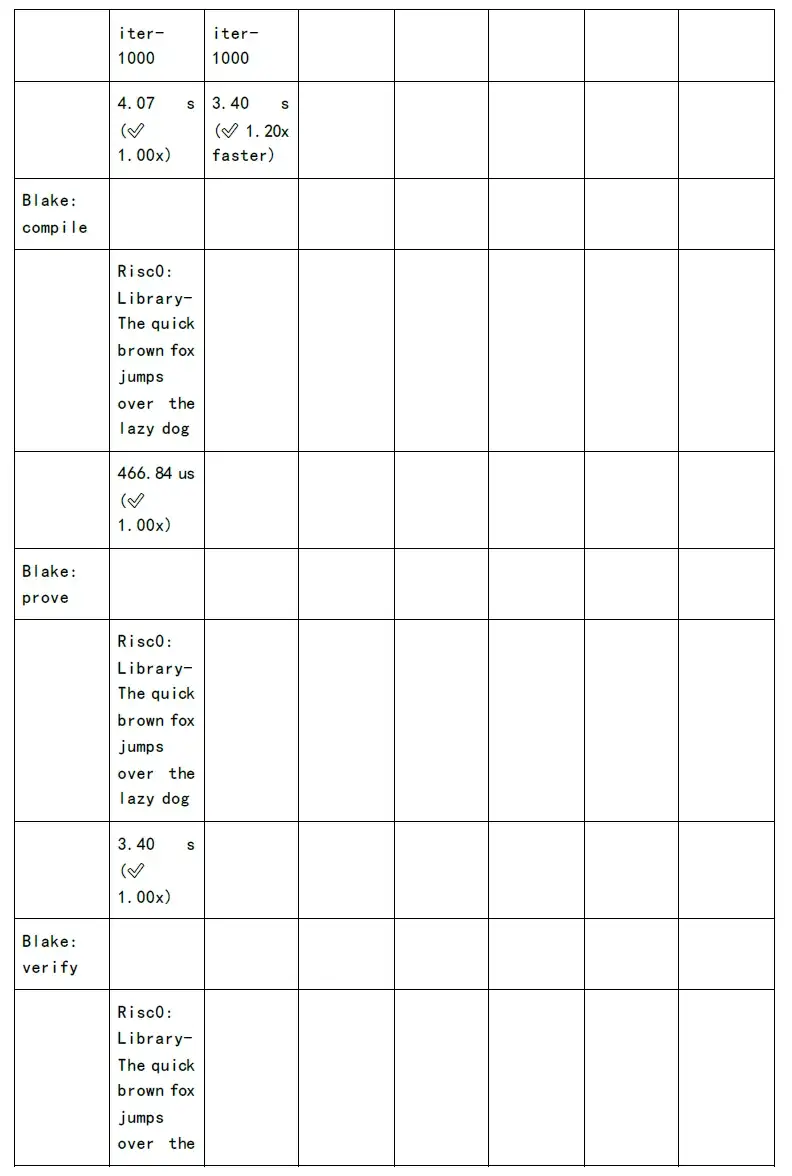
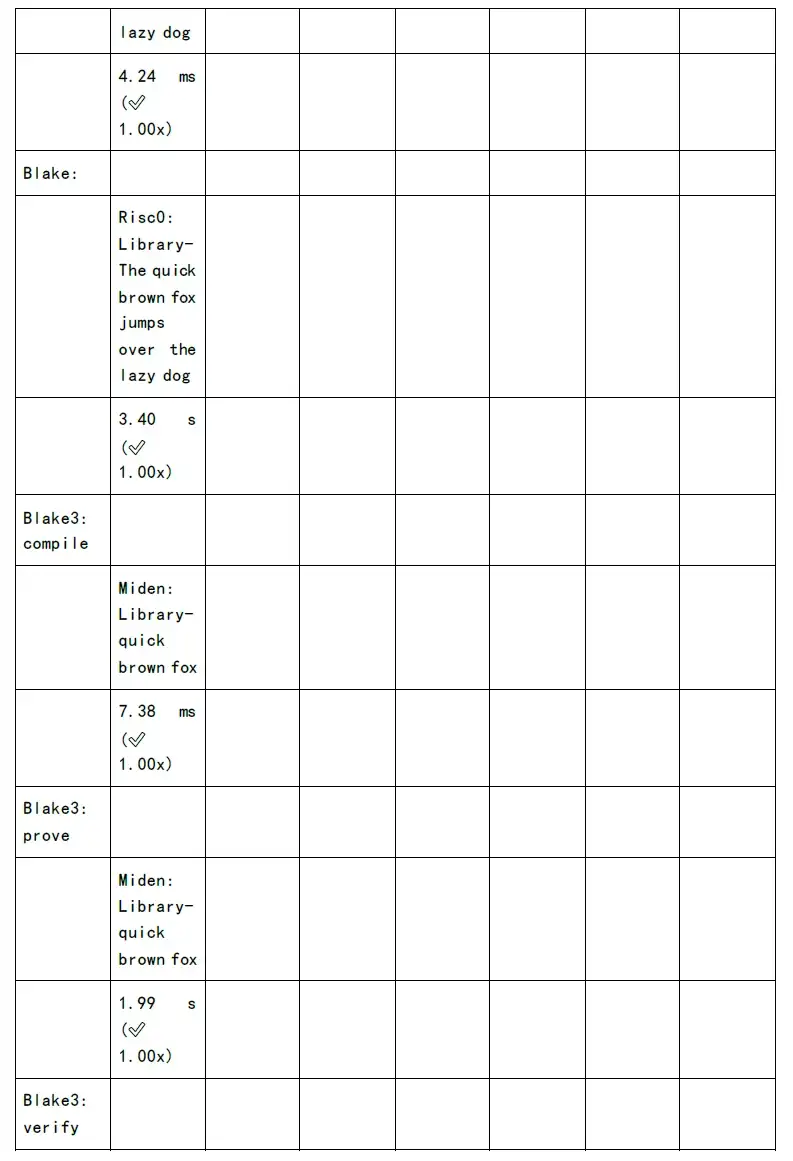
但是NTT 和MSM 計算時間開銷,還是居高不下。如果希望給用戶減少等待時間,提升使用體驗效果,必須要在數學實現上、軟件架構優化、GPU/FPGA/ASIC 等等層面進行加速。
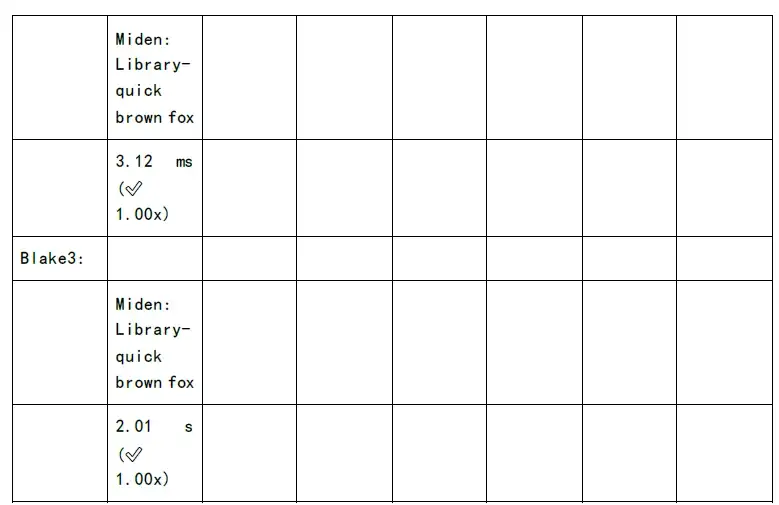
下圖為各個zkSnark 家族算法的證明生成時間和驗證時間的測試:
二級標題
二級標題
二級標題
二級標題
二級標題
二級標題
二級標題
二級標題
一級標題
一級標題
一級標題



