Giới thiệu: Cơ chế cốt lõi của Gonka PoW 2.0

Ý tưởng cốt lõi của Gonka PoW 2.0 là chuyển đổi bằng chứng công việc truyền thống thành một tác vụ tính toán AI có ý nghĩa. Bài viết này sẽ đi sâu vào hai cơ chế cốt lõi của nó: tạo thử thách tính toán và xác minh chống gian lận. Bài viết sẽ chứng minh cách cơ chế đồng thuận sáng tạo này đảm bảo tính hữu ích tính toán đồng thời thiết lập một biện pháp bảo vệ chống gian lận đáng tin cậy.

Toàn bộ quá trình có thể được tóm tắt như sơ đồ sau: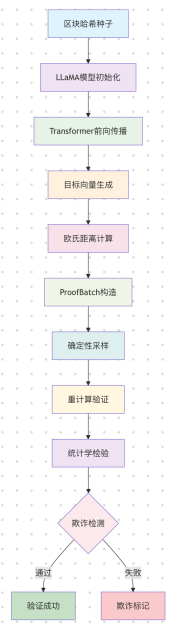

1. Cơ chế tạo thách thức tính toán

Các thách thức tính toán là cốt lõi của Gonka PoW 2.0, biến bằng chứng công việc truyền thống thành một tác vụ tính toán AI có ý nghĩa. Không giống như PoW truyền thống, thách thức tính toán của Gonka không chỉ là một phép tính băm đơn giản, mà là một quy trình suy luận học sâu hoàn chỉnh, không chỉ đảm bảo an ninh mạng mà còn tạo ra các kết quả tính toán hữu ích.

1.1 Quản lý thống nhất hệ thống hạt giống

Tất cả các phép tính đều được điều khiển bởi một hạt giống thống nhất, đảm bảo tất cả các nút trong mạng đều thực hiện cùng một tác vụ tính toán. Thiết kế này đảm bảo tính tái tạo và công bằng trong các phép tính, vì mọi nút phải thực hiện cùng một tác vụ tính toán để có được kết quả hợp lệ.

Nguồn dữ liệu : mlnode/packages/pow/src/pow/compute/compute.py#L217-L225

Các yếu tố chính của hệ thống hạt giống bao gồm:

-Băm khối : hoạt động như hạt giống chính để đảm bảo tính nhất quán của các tác vụ tính toán

-Khóa công khai: xác định danh tính của nút tính toán

- Chiều cao khối : đảm bảo đồng bộ thời gian

- Cấu hình tham số: kiến trúc mô hình điều khiển và độ phức tạp tính toán

1.2 Khởi tạo xác định các trọng số mô hình LLaMA

Mỗi tác vụ tính toán đều bắt đầu bằng một kiến trúc mô hình LLaMA thống nhất, với các trọng số được khởi tạo xác định thông qua băm khối. Thiết kế này đảm bảo tất cả các nút đều sử dụng cùng một cấu trúc mô hình và trọng số ban đầu, đảm bảo kết quả tính toán nhất quán.

Nguồn dữ liệu : mlnode/packages/pow/src/pow/models/llama31.py#L32-L51

Nguyên lý toán học của việc khởi tạo trọng số:

- Phân phối chuẩn: N(0, 0,02²) - Phương sai nhỏ đảm bảo độ ổn định của gradient

- Chủ nghĩa quyết định : Cùng một khối băm tạo ra cùng một trọng số

- Hiệu quả bộ nhớ: hỗ trợ độ chính xác float16 để giảm mức sử dụng bộ nhớ video

1.3 Tạo vectơ mục tiêu và tính toán khoảng cách

Các vectơ mục tiêu được phân bố đều trên mặt cầu đơn vị nhiều chiều, đây chính là chìa khóa cho tính công bằng của bài toán tính toán. Bằng cách tạo ra các vectơ mục tiêu phân bố đều trong không gian nhiều chiều, tính ngẫu nhiên và công bằng của bài toán tính toán được đảm bảo.

Nguồn dữ liệu : mlnode/packages/pow/src/pow/random.py#L165-L177

Trong không gian từ vựng 4096 chiều, hình học cầu có các tính chất sau:

- Đơn vị độ dài :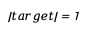

- Phân bố góc: Góc giữa hai vectơ ngẫu nhiên bất kỳ có xu hướng là 90°

- Hiện tượng tập trung : phần lớn khối lượng phân bố gần bề mặt quả cầu

Nguyên lý toán học của sự phân bố đều trên một quả cầu:

Trong không gian n chiều, sự phân bố đồng đều trên mặt cầu đơn vị có thể được tạo ra như sau:

1. Đầu tiên tạo n biến ngẫu nhiên phân phối chuẩn chuẩn độc lập: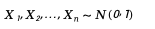

2. Sau đó chuẩn hóa: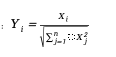

Phương pháp này đảm bảo rằng các vectơ được tạo ra được phân bố đều trên hình cầu và biểu thức toán học là:

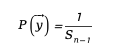
TRONG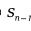 là diện tích bề mặt của hình cầu n-1.

Tính toán khoảng cách là một bước quan trọng trong việc kiểm chứng kết quả tính toán. Hiệu quả của phép tính được đo lường bằng cách tính khoảng cách Euclidean giữa đầu ra của mô hình và vectơ mục tiêu:

Nguồn dữ liệu : Dựa trên logic xử lý trong mlnode/packages/pow/src/pow/compute/compute.py

Các bước tính khoảng cách:

1. Ứng dụng hoán vị : sắp xếp lại các chiều đầu ra theo hạt giống hoán vị

2. Chuẩn hóa vectơ : Đảm bảo rằng tất cả các vectơ đầu ra nằm trên hình cầu đơn vị

3. Tính toán khoảng cách : Tính khoảng cách Euclid đến vectơ mục tiêu

4. Đóng gói hàng loạt : đóng gói kết quả vào cấu trúc dữ liệu ProofBatch

2. Cơ chế xác minh chống gian lận

Để đảm bảo tính công bằng và bảo mật của các thử thách tính toán, hệ thống đã thiết kế một hệ thống xác minh chống gian lận tinh vi. Cơ chế này xác minh tính xác thực của các phép tính thông qua lấy mẫu xác định và kiểm tra thống kê, ngăn chặn các nút độc hại thu lợi bất chính thông qua gian lận.

2.1 Cấu trúc dữ liệu ProofBatch

Kết quả tính toán được đóng gói vào cấu trúc dữ liệu ProofBatch, là bộ phận cốt lõi của quy trình xác minh. ProofBatch chứa thông tin nhận dạng của nút tính toán, dấu thời gian và kết quả tính toán, cung cấp nền tảng dữ liệu cần thiết cho việc xác minh tiếp theo.

Nguồn dữ liệu : mlnode/packages/pow/src/pow/data.py#L8-L25

Đặc điểm của cấu trúc dữ liệu ProofBatch:

-Identity : public_key xác định duy nhất nút tính toán

- Liên kết chuỗi khối : block_hash và block_height đảm bảo đồng bộ hóa thời gian

-Kết quả tính toán : nonces và dist ghi lại tất cả các lần thử và giá trị khoảng cách của chúng

- Hỗ trợ từng đợt : hỗ trợ trích xuất các phép tính thành công đáp ứng ngưỡng

2.2 Cơ chế lấy mẫu xác định

Để cải thiện hiệu quả xác minh, hệ thống sử dụng cơ chế lấy mẫu xác định, chỉ xác minh một số kết quả tính toán thay vì tất cả. Thiết kế này không chỉ đảm bảo hiệu quả xác minh mà còn giảm đáng kể chi phí xác minh.

Tỷ lệ lấy mẫu xác minh của Gonka được quản lý thống nhất thông qua các tham số trên chuỗi để đảm bảo tính nhất quán trên toàn bộ mạng:

Nguồn dữ liệu : inference-chain/proto/inference/inference/params.proto#L75-L78

Nguồn dữ liệu : inference-chain/x/inference/types/params.go#L129-L133

Dựa trên hệ thống hạt giống, quy trình lấy mẫu hoàn toàn mang tính xác định, đảm bảo tính công bằng của việc xác minh. Bằng cách sử dụng hàm băm SHA-256 và khóa công khai của trình xác thực, hàm băm khối, chiều cao khối và các thông tin khác để tạo hạt giống, tất cả trình xác thực đều được đảm bảo sử dụng cùng một chiến lược lấy mẫu:

Nguồn dữ liệu : decentralized-api/mlnodeclient/poc.go#L175-L201

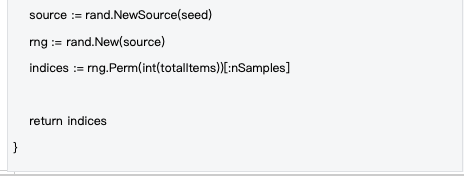
Ưu điểm của lấy mẫu xác định:

- Công bằng : Tất cả các trình xác thực đều sử dụng cùng một chiến lược lấy mẫu

- Hiệu quả : Chỉ xác minh một phần dữ liệu để giảm chi phí xác minh

- Bảo mật : Khó có thể dự đoán dữ liệu được lấy mẫu để ngăn chặn gian lận

2.3 Phát hiện gian lận thống kê

Hệ thống sử dụng kiểm định phân phối nhị thức để phát hiện gian lận, sử dụng các phương pháp thống kê để xác định tính trung thực của các nút tính toán. Phương pháp này đặt ra tỷ lệ lỗi dự kiến dựa trên độ chính xác của phần cứng và độ phức tạp tính toán, đồng thời sử dụng các kiểm định thống kê để phát hiện các điểm bất thường.

Nguồn dữ liệu : mlnode/packages/pow/src/pow/data.py#L7

Tỷ lệ lỗi dự kiến được thiết lập có tính đến các yếu tố sau:

- Độ chính xác dấu phẩy động: Sự khác biệt về độ chính xác dấu phẩy động giữa các phần cứng khác nhau

- Tính toán song song : Lỗi tích lũy số do song song hóa GPU gây ra

- Tính ngẫu nhiên : sự khác biệt nhỏ trong khởi tạo trọng số mô hình

-Sự khác biệt về hệ thống: sự khác biệt về hành vi tính toán giữa các hệ điều hành và trình điều khiển khác nhau

Nguồn dữ liệu : mlnode/packages/pow/src/pow/data.py#L174-L204

Tóm tắt: Xây dựng mạng lưới điện toán AI an toàn và đáng tin cậy

Gonka PoW 2.0 kết hợp thành công các yêu cầu bảo mật của blockchain với giá trị thực tiễn của AI thông qua một thử thách tính toán được thiết kế cẩn thận và cơ chế xác minh chống gian lận. Thử thách tính toán đảm bảo tính ý nghĩa của công việc, trong khi cơ chế chống gian lận đảm bảo tính công bằng và bảo mật của mạng lưới.

Thiết kế này không chỉ xác minh tính khả thi về mặt kỹ thuật của "khai thác có ý nghĩa" mà còn thiết lập một tiêu chuẩn mới cho điện toán AI phân tán: điện toán phải vừa an toàn vừa hữu ích, có thể xác minh và hiệu quả.

Bằng cách kết hợp thống kê, mật mã và thiết kế hệ thống phân tán, Gonka PoW 2.0 đã thiết lập thành công cơ chế chống gian lận đáng tin cậy đồng thời đảm bảo tính hữu ích về mặt tính toán, cung cấp nền tảng bảo mật vững chắc cho lộ trình kỹ thuật "khai thác có ý nghĩa".

Lưu ý: Bài viết này dựa trên tài liệu thiết kế và triển khai mã thực tế của dự án Gonka. Tất cả các thông số phân tích kỹ thuật và cấu hình đều được lấy từ kho mã chính thức của dự án.

Giới thiệu về Gonka.ai

Gonka là một mạng lưới phi tập trung được thiết kế để cung cấp sức mạnh tính toán AI hiệu quả. Mục tiêu thiết kế của nó là tối đa hóa việc sử dụng sức mạnh tính toán GPU toàn cầu để hoàn thành khối lượng công việc AI có ý nghĩa. Bằng cách loại bỏ các cổng kiểm soát tập trung, Gonka cung cấp cho các nhà phát triển và nhà nghiên cứu quyền truy cập không cần cấp phép vào tài nguyên điện toán, đồng thời thưởng cho tất cả người tham gia bằng token GNK gốc.

Gonka được ươm mầm bởi công ty phát triển AI Product Science Inc. của Mỹ. Được thành lập bởi anh em nhà Libermans, những người kỳ cựu trong ngành Web 2 và cựu giám đốc sản phẩm cốt lõi tại Snap Inc., công ty đã huy động thành công 18 triệu đô la vào năm 2023 từ các nhà đầu tư, bao gồm Coatue Management, nhà đầu tư của OpenAI, Slow Ventures, nhà đầu tư của Solana, K5, Insight và Benchmark Partners. Những người đóng góp ban đầu cho dự án bao gồm các công ty hàng đầu trong lĩnh vực Web 2-Web 3, chẳng hạn như 6 Blocks, Hard Yaka, Gcore và Bitfury.

Trang web chính thức | Github | X | Discord | Sách trắng | Mô hình kinh tế | Hướng dẫn sử dụng