Tiếp nối chương trước, chúng tôi đã xuất bản ba bài trong loạt bài về Xây dựng danh mục tài sản tiền điện tử mạnh mẽ bằng cách sử dụng mô hình đa yếu tố:Cơ sở lý thuyết、Tiền xử lý dữ liệu、Kiểm tra tính hợp lệ của yếu tố。

Ba bài viết đầu tiên giải thích lý thuyết về chiến lược đa yếu tố và các bước thử nghiệm một yếu tố tương ứng.

1. Lý do kiểm định tương quan nhân tố: đa cộng tuyến

Chúng tôi sàng lọc một loạt các yếu tố hiệu quả thông qua thử nghiệm một yếu tố, nhưng các yếu tố trên không thể nhập trực tiếp vào cơ sở dữ liệu. Bản thân các yếu tố có thể được chia thành nhiều loại lớn theo ý nghĩa kinh tế cụ thể, giữa các yếu tố cùng loại có mối tương quan chặt chẽ, nếu chúng được nhập trực tiếp vào cơ sở dữ liệu mà không sàng lọc tương quan và thực hiện hồi quy tuyến tính bội để tính tỷ suất lợi nhuận kỳ vọng. tùy thuộc vào các yếu tố khác nhau sẽ xảy ra hiện tượng đa cộng tuyến. Trong kinh tế lượng, đa cộng tuyến có nghĩa là một số hoặc tất cả các biến giải thích trong mô hình hồi quy có mối quan hệ tuyến tính hoàn chỉnh hoặc chính xác (tương quan cao giữa các biến).

Vì vậy, sau khi sàng lọc các nhân tố hiệu quả, trước tiên cần tiến hành kiểm định T về mối tương quan giữa các nhân tố theo loại chính, đối với những nhân tố có tương quan cao hơn thì loại bỏ những nhân tố có ý nghĩa thấp hơn hoặc thực hiện tổng hợp nhân tố.

Giải thích toán học về đa cộng tuyến như sau:

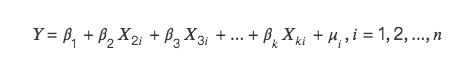
Sẽ có hai tình huống:

Hậu quả của đa cộng tuyến:

1. Công cụ ước tính tham số không tồn tại trong điều kiện cộng tuyến hoàn hảo

2. Công cụ ước tính OLS không hợp lệ trong trường hợp cộng tuyến gần đúng

3. Ý nghĩa kinh tế của công cụ ước lượng tham số là không hợp lý

4. Kiểm định ý nghĩa của biến (t test) mất ý nghĩa

5. Chức năng dự đoán của mô hình không thành công: tỷ suất lợi nhuận dự đoán được trang bị bởi mô hình tuyến tính đa biến là cực kỳ không chính xác và mô hình không thành công.

2. Bước 1: Kiểm định tương quan các yếu tố cùng loại

Kiểm tra mối tương quan giữa các hệ số mới tính toán và các hệ số đã có trong cơ sở dữ liệu. Nói chung, có hai loại dữ liệu tương quan:

1. Tính toán mối tương quan dựa trên giá trị hệ số của tất cả các token trong giai đoạn backtest

2. Tính toán mối tương quan dựa trên giá trị lợi nhuận vượt quá hệ số của tất cả các token trong giai đoạn backtest

Mỗi yếu tố chúng tôi tìm kiếm đều có sự đóng góp và khả năng giải thích nhất định đối với tỷ lệ hoàn vốn của mã thông báo. Mục đích của việc tiến hành thử nghiệm tương quan** là tìm ra các yếu tố có cách giải thích và đóng góp khác nhau vào lợi nhuận của chiến lược. Mục tiêu cuối cùng của chiến lược là lợi nhuận**. Nếu hai yếu tố mô tả trả về giống nhau thì sẽ vô nghĩa ngay cả khi giá trị của hai yếu tố đó khác nhau đáng kể. Do đó, chúng tôi không muốn tìm các nhân tố có sự khác biệt lớn về giá trị nhân tố mà muốn tìm các nhân tố có các nhân tố khác nhau mô tả lợi nhuận nên cuối cùng chúng tôi chọn sử dụng giá trị lợi nhuận vượt quá nhân tố để tính toán mối tương quan.

Chiến lược của chúng tôi là tần suất hàng ngày, vì vậy chúng tôi tính toán ma trận hệ số tương quan giữa lợi nhuận vượt quá của yếu tố dựa trên ngày của khoảng thời gian kiểm tra lại.

Lập trình giải quyết n yếu tố hàng đầu có mối tương quan cao nhất trong thư viện:

def get_n_max_corr(self, factors, n= 1):
       factors_excess = self.get_excess_returns(factors)
       save_factor_excess = self.get_excess_return(self.factor_value, self.start_date, self.end_date)
       if len(factors_excess) < 1:
           return factor_excess, 1.0, None
       factors_excess[self.factor_name] = factor_excess['excess_return']
       factors_excess = pd.concat(factors_excess, axis= 1)
       factors_excess.columns = factors_excess.columns.levels[ 0 ]
       # get corr matrix
       factor_corr = factors_excess.corr()
       factor_corr_df = factor_corr.abs().loc[self.factor_name]
       max_corr_score = factor_corr_df.sort_values(ascending=False).iloc[ 1:].head(n)
       
       return save_factor_excess, factor_corr_df, max_corr_score

3. Bước 2: Lựa chọn nhân tố và tổng hợp nhân tố

Đối với các tập nhân tố có độ tương quan cao, có hai cách xử lý:

(1) Lựa chọn yếu tố

Dựa trên giá trị ICIR, năng suất, tỷ lệ doanh thu và tỷ lệ Sharpe của chính yếu tố đó, các yếu tố hiệu quả nhất trong một chiều nhất định sẽ được chọn để giữ lại và các yếu tố khác sẽ bị xóa.

(2) Tổng hợp yếu tố

Tổng hợp các yếu tố trong bộ yếu tố và lưu giữ càng nhiều thông tin hiệu quả càng tốt trên mặt cắt ngang

Giả sử hiện tại có 3 ma trận nhân tố cần được xử lý:

2.1 Trọng số bằng nhau

Trọng số của từng yếu tố bằng nhau (w=1/số yếu tố) và yếu tố toàn diện = tổng các giá trị của từng yếu tố được lấy trung bình.

Ví dụ: Các yếu tố động lượng, tỷ suất lợi nhuận một tháng, tỷ suất lợi nhuận hai tháng, tỷ suất lợi nhuận ba tháng, tỷ suất lợi nhuận sáu tháng, tỷ suất lợi nhuận mười hai tháng. Hệ số tải nhân tố của sáu yếu tố này đều chiếm 1/6 trọng lượng. , tổng hợp tải hệ số động lượng mới và sau đó thực hiện lại quá trình chuẩn hóa.

tổng hợp 1 = tổng hợp.mean(axis= 1) # Tìm giá trị trung bình theo hàng

2.2 Trọng số IC lịch sử, ICIR lịch sử, trọng số thu nhập lịch sử

Các yếu tố được tính trọng số theo giá trị IC của chúng (giá trị ICIR, giá trị trả về lịch sử) trong khoảng thời gian backtest. Đã có nhiều thời kỳ trong quá khứ và mỗi thời kỳ có một giá trị IC, do đó giá trị trung bình của chúng được sử dụng làm trọng số của hệ số. Người ta thường sử dụng giá trị trung bình (trung bình số học) của IC trong giai đoạn backtest làm trọng số.

2.3 Trọng số nửa đời IC lịch sử, trọng số nửa đời ICIR lịch sử

Cả 2.1 và 2.2 đều tính giá trị trung bình số học và mỗi IC và ICIR trong giai đoạn kiểm tra lại đều có tác động như nhau đối với hệ số theo mặc định.

Tuy nhiên, trên thực tế, tác động của từng giai đoạn của giai đoạn backtest đến giai đoạn hiện tại là không hoàn toàn giống nhau và có sự suy giảm về mặt thời gian. Khoảng thời gian càng gần với thời kỳ hiện tại thì tác động càng lớn và tác động càng xa thì tác động càng nhỏ. Dựa trên nguyên tắc này, trước khi tính trọng lượng IC, trước tiên hãy xác định trọng lượng chu kỳ bán rã, càng gần chu kỳ hiện tại thì giá trị trọng lượng càng lớn, càng xa thì trọng lượng càng nhỏ.

Đạo hàm toán học của trọng lượng nửa đời:

2.4 Tối đa hóa trọng số ICIR

Bằng cách giải phương trình, tính trọng số hệ số w tối ưu để tối đa hóa ICIR

Bài toán ước lượng ma trận hiệp phương sai: Ma trận hiệp phương sai được sử dụng để đo lường mối tương quan giữa các tài sản khác nhau. Trong thống kê, ma trận hiệp phương sai mẫu thường được sử dụng thay cho ma trận hiệp phương sai tổng thể, tuy nhiên khi cỡ mẫu không đủ thì ma trận hiệp phương sai mẫu và ma trận hiệp phương sai tổng thể sẽ rất khác nhau. Vì vậy, có người đã đề xuất một phương pháp ước lượng nén, nguyên tắc là giảm thiểu sai số bình phương trung bình giữa ma trận hiệp phương sai ước lượng và ma trận hiệp phương sai thực tế.

Đường:

1. Ma trận hiệp phương sai mẫu

2. Độ co Ledoit-Wolf: Đưa ra hệ số co ngót để trộn ma trận hiệp phương sai ban đầu với ma trận nhận dạng để giảm tác động của nhiễu.

3. Độ co xấp xỉ của Oracle: Một cải tiến so với độ co rút của Ledoit-Wolf, mục tiêu là ước tính chính xác hơn ma trận hiệp phương sai thực khi kích thước mẫu nhỏ bằng cách điều chỉnh ma trận hiệp phương sai. (Việc triển khai lập trình giống như cách rút gọn Ledoit-Wolf)

2.5 Phân tích thành phần chính PCA

Phân tích thành phần chính (PCA) là một phương pháp thống kê được sử dụng để giảm kích thước và trích xuất các tính năng chính của dữ liệu. Mục tiêu là ánh xạ dữ liệu gốc sang hệ tọa độ mới thông qua phép biến đổi tuyến tính để tối đa hóa phương sai của dữ liệu trong hệ tọa độ mới.

Cụ thể, trước tiên PCA tìm các thành phần chính trong dữ liệu, là hướng có phương sai lớn nhất trong dữ liệu. Sau đó, nó tìm thành phần chính thứ hai trực giao (không liên quan) với thành phần chính thứ nhất và có phương sai lớn nhất. Quá trình này được lặp lại cho đến khi tìm thấy tất cả các thành phần chính trong dữ liệu.