Nhóm tiền thưởng nghiên cứu DAOrayaki DAO:

Địa chỉ tài trợ: DAOrayaki.eth

Nhóm tiền thưởng nghiên cứu DAOrayaki DAO:

Địa chỉ tài trợ: DAOrayaki.eth

Tiến trình bỏ phiếu: Ủy ban DAO 2/0 thông qua

Loại nghiên cứu: Bằng chứng kiến ​​thức không có chuỗi khối

zkSNARK là một cách để tạo bằng chứng không có kiến ​​thức. Cụ thể, các phương pháp ngắn gọn, không tương tác để tạo bằng chứng không kiến ​​thức.

Tác giả gốc: Kobi Gurkan

zkSNARK là một cách để tạo bằng chứng không có kiến ​​thức. Cụ thể, các phương pháp ngắn gọn, không tương tác để tạo bằng chứng không kiến ​​thức.

https://z.cash/technology/zksnarks/

zkSNARKs chính xác là gì có thể tham khảo sau

1. Cách zkSNARK được xây dựng trong Zcash - với sự giúp đỡ của nhóm Zcash.

https://qed-it.com/trustless-computing-on-private-data/

2. Điện toán không cần tin cậy cho dữ liệu cá nhân - Daniel Benarroch và Aviv Zohar, Giám đốc mật mã học tại QED-it

Bài đăng trên blog của giáo sư.

https://qed-it.com/2017/07/04/zkp-in-action/

3. Bằng chứng, chuỗi khối. ZKPinAction - Phiên giải thích về ZKP và cách tạo ZKP cho Sudoku

https://qed-it.com/2017-12-20-the-incredible-machine/

băng hình.

https://qed-it.com/2017/07/11/the-hunting-of-the-snark/

4. Cỗ máy đáng kinh ngạc - Một bài đăng trên blog của Giáo sư Aviv Zohar, Nhà khoa học trưởng của QED-it, giải thích về cách thiết lập đáng tin cậy.

5. Săn SNARK - Một loạt câu đố để thử nghiệm với ZKP.

Tại QED-it, chúng tôi sử dụng zkSNARK và các công cụ khác để tạo chuỗi khối không kiến ​​thức cho doanh nghiệp.

Có lẽ việc triển khai sản xuất zkSNARK được biết đến nhiều nhất là ZCash - một loại tiền điện tử với các giao dịch không thể liên kết và số tiền ẩn. ZCash, cũng như một số sản phẩm khác sử dụng zkSNARK, dựa trên cấu trúc có tên là Pinnochio, mặc dù cụ thể hơn là BCTV14a. Đó là một phần công nghệ tuyệt vời, như bạn có thể nghi ngờ. Cấu trúc này có một nhược điểm rõ ràng: thiết lập đáng tin cậy."cài đặt đáng tin cậy"Thiết lập là quá trình tạo CRS (Chuỗi tham chiếu chung) hay được biết đến rộng rãi hơn là một cặp khóa xác minh và chứng nhận. Những cái này

chìa khóa"Trình chứng minh và trình xác minh được sử dụng để tạo và xác minh bằng chứng về một vấn đề cụ thể (hoặc hệ thống ràng buộc), tương ứng."Trong quá trình này, một số yếu tố ngẫu nhiên được lấy mẫu nhưng phải được giữ bí mật. Bởi vì nếu những người xác minh biết điều này, họ sẽ có thể tạo ra các bằng chứng đã được xác minh thành công mà không cần sử dụng giải pháp thực tế cho vấn đề trong quy trình chứng minh. Nói cách khác, để làm sai lệch bằng chứng và làm suy yếu tính đúng đắn. Sự ngẫu nhiên này còn được gọi là

. Có nhiều cách để tránh mối lo ngại này bằng cách không đặt niềm tin vào một thực thể duy nhất. Đối với các mạch công cộng, các phương pháp này thường liên quan đến tính toán của nhiều bên, trong đó nhiều người tham gia đóng góp tính ngẫu nhiên của họ, tính ngẫu nhiên này sau đó sẽ bị hủy. Thật thú vị, miễn là một người tham gia trung thực và tính ngẫu nhiên của họ bị loại bỏ, toàn bộ quá trình sẽ an toàn.

1. "The Ceremony "tệp âm thanh

https://www.wnycstudios.org/podcasts/radiolab/articles/ceremony

Một số ví dụ đáng chú ý về các thiết lập đáng tin cậy sử dụng MPC vẫn là: ZCash.

https://z.cash.foundation/blog/powers-of-tau/

tệp âm thanh"Tau"2. Sức mạnh của Tàu

Bạn có thể nhận thấy điều này xuất hiện ở đây

...Bí mật của Tau rất quan trọng. Một khi Tau đã biết câu tục ngữ, thì rất dễ giả mạo bằng chứng.

tạo chứng chỉ

Chúng ta hãy xem nhanh cách xây dựng được đề xuất trong BCTV14a."Đây là một bài toán, chúng ta hãy chọn ra những chi tiết có liên quan đến bài viết này:"1. Tau là một điểm trong trường hữu hạn được vẽ ngẫu nhiên trong quá trình thiết lập và là

chất thải độc hại"a*b=c "phần của nó."a*b-c=0"。

2. Trong quá trình chứng minh, người xác minh tính toán một số đa thức - A(z), B(z) và C(z) từ nghiệm của hệ thống ràng buộc và các đầu vào công khai và riêng tư. Về cơ bản, các đa thức này đại diện cho"ràng buộc của hình thức, hoặc tương đương"H(z)--H(Tau)。

3. Trình xác minh cũng tính toán H(z)=(A(z)B(z)-C(z))/Z(z), trong đó Z(z) là một đa thức công khai tại các điểm đại diện cho hệ thống ràng buộc bằng 0. Lưu ý rằng vì A, B và C tính đến đầu vào của người xác minh, H chỉ có thể được tính nếu tử số cũng bằng 0 tại cùng một điểm, chứng tỏ rằng người xác minh thực sự biết giải pháp cho vấn đề mang lại A*BC = 0 . Phần quan trọng bây giờ xảy ra - không cần biết Tau, người xác minh có thể tính toán

trong chỉ mục

Tại sao chúng ta làm việc này? Bởi vì bằng cách đánh giá tại một điểm ngẫu nhiên Tau, người chứng minh có xác suất cao cho thấy rằng phương trình H=(A*BC)/Z đúng với mọi Z. Ở một góc nhìn khác về cùng một vấn đề, nếu không biết Tau, thì khả năng cao là người chứng minh sẽ không thể tạo ra một đa thức có giá trị chính xác như vậy tại điểm đó.

Làm thế nào để chúng tôi làm điều này về mặt kỹ thuật? Có một thực tế là một phần của quy trình thiết lập tạo ra các phần tử chứa tất cả các lũy thừa liên quan của Tau ẩn trong số mũ, được cho là pk_Hi. Nếu chúng ta có các hệ số của H, chúng ta có thể kết hợp các hệ số này và tạo ra H(Tau).

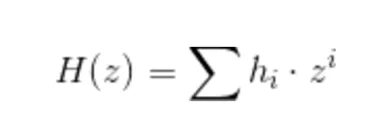
cụ thể hơn

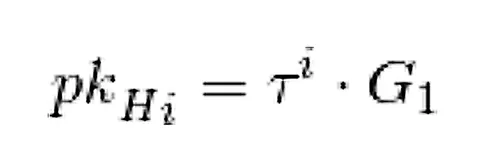
H(z) được tính toán bởi người xác minh

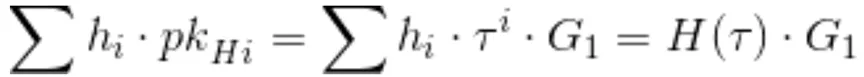
khóa được lấy từ chứng thực, được tính toán trong quá trình thiết lập

Đánh giá "theo cấp số mũ" của H(Tau)

Sau khi nhận được bằng chứng, người xác minh có thể kiểm tra lại theo số mũ xem người xác minh có thực sự cung cấp hệ số H thỏa mãn mối quan hệ H=(A*BC)/Z hay không, điều này chỉ có thể được thực hiện nếu người xác minh thực sự biết một giải pháp.

chứng chỉ giả mạo

Bây giờ hãy đặt ra một giả thuyết, nếu Tàu biết thì sao? Nếu vì lý do nào đó, nó đã bị lộ trong quá trình thiết lập và được biết bởi trình xác thực độc hại.

Rõ ràng, rất dễ dàng để giả mạo một bằng chứng. Vì việc kiểm tra tính tương đương cho H=(A*BC)/Z được thực hiện tại một điểm cụ thể Tau, nên chúng ta có thể sử dụng những gì chúng ta biết về Tau để tạo một đa thức thỏa mãn chính xác. Nghĩa là, tạo một đa thức hằng H(z) đơn giản luôn trả về (A(Tau)*B(Tau)-C(Tau))/Z(Tau).

Cuộc kiểm tra của thanh tra viên sẽ trôi qua và không ai biết. nghe có vẻ khó...

Không có gì. Rất hoan nghênh bạn kiểm tra mã chứng minh khái niệm này, dựa trên libsnarktutorial của Howard Wu và tự mình xem các sửa đổi được thực hiện đối với mã.

1. Chương trình thiết lập mạch phân rã bit mặc dù là C.

3. Trình xác minh tải Tau từ đĩa và chứng minh với đầu vào sai. Trình xác minh, biết Tau, tạo ra một đa thức không đổi bất kể đầu vào là gì.

Tóm lại là

Người xác minh sau đó xác minh thành công bằng chứng!"Tóm lại là"Tôi hy vọng bài đăng này cung cấp một số thông tin chi tiết về những gì mọi người đang nói về zkSNARK