บทนำ: กลไกหลักของ Gonka PoW 2.0

แนวคิดหลักของ Gonka PoW 2.0 คือการเปลี่ยนกระบวนการพิสูจน์การทำงาน (proof-of-work) แบบเดิมให้กลายเป็นงานประมวลผล AI ที่มีความหมาย บทความนี้จะเจาะลึกกลไกหลักสองประการ ได้แก่ การสร้างความท้าทายเชิงคำนวณ (computational challenge creation) และการตรวจสอบป้องกันการโกง (anti-cheating verification) โดยจะแสดงให้เห็นว่ากลไกฉันทามติเชิงนวัตกรรมนี้ช่วยให้มั่นใจถึงประโยชน์ในการประมวลผลได้อย่างไร พร้อมกับสร้างระบบป้องกันการโกงที่เชื่อถือได้

กระบวนการทั้งหมดสามารถสรุปได้ดังแผนภาพต่อไปนี้: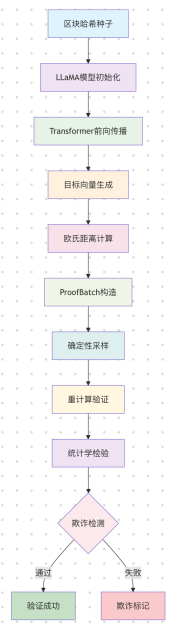

1. กลไกการสร้างความท้าทายในการคำนวณ

ความท้าทายด้านการประมวลผลคือหัวใจสำคัญของ Gonka PoW 2.0 ซึ่งเปลี่ยนกระบวนการพิสูจน์การทำงานแบบเดิมให้กลายเป็นงานประมวลผล AI ที่มีความหมาย ความท้าทายด้านการประมวลผลของ Gonka แตกต่างจาก PoW ทั่วไป ไม่ใช่การคำนวณแฮชแบบง่ายๆ แต่เป็นกระบวนการคิดหาเหตุผลเชิงลึกแบบสมบูรณ์ ซึ่งไม่เพียงแต่รับประกันความปลอดภัยของเครือข่ายเท่านั้น แต่ยังให้ผลลัพธ์เชิงคำนวณที่ใช้งานได้จริงอีกด้วย

1.1 การจัดการระบบเมล็ดพันธุ์แบบรวมศูนย์

การคำนวณทั้งหมดขับเคลื่อนโดย seed เดียว เพื่อให้แน่ใจว่าทุกโหนดในเครือข่ายทำงานคำนวณเดียวกัน การออกแบบนี้ช่วยให้มั่นใจได้ถึงความสามารถในการทำซ้ำและความยุติธรรมในการคำนวณ เนื่องจากทุกโหนดต้องทำงานคำนวณเดียวกันเพื่อให้ได้ผลลัพธ์ที่ถูกต้อง

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/compute/compute.py#L217-L225

องค์ประกอบหลักของระบบเมล็ดพันธุ์ ได้แก่:

-Block hash : ทำหน้าที่เป็น master seed เพื่อให้แน่ใจว่างานการประมวลผลมีความสอดคล้องกัน

- คีย์ สาธารณะ: ระบุตัวตนของโหนดการประมวลผล

-ความสูงของบล็อก : รับรองการซิงโครไนซ์เวลา

- การกำหนดค่า พารามิเตอร์: สถาปัตยกรรมโมเดลควบคุมและความซับซ้อนในการคำนวณ

1.2 การเริ่มต้นแบบกำหนดของน้ำหนักแบบจำลอง LLaMA

งานคำนวณแต่ละงานเริ่มต้นด้วยสถาปัตยกรรมแบบจำลอง LLaMA แบบรวมศูนย์ โดยน้ำหนักจะถูกกำหนดค่าเริ่มต้นแบบตายตัวผ่านการแฮชแบบบล็อก การออกแบบนี้ช่วยให้มั่นใจได้ว่าทุกโหนดจะใช้โครงสร้างแบบจำลองและน้ำหนักเริ่มต้นเดียวกัน ซึ่งรับประกันผลลัพธ์การคำนวณที่สอดคล้องกัน

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/models/llama31.py#L32-L51

หลักการทางคณิตศาสตร์ของการกำหนดค่าเริ่มต้นน้ำหนัก:

- การแจกแจง แบบปกติ: N(0, 0.02²) - ความแปรปรวนขนาดเล็กช่วยให้มั่นใจถึงความเสถียรของการไล่ระดับ

- การกำหนดล่วงหน้า : แฮชบล็อกเดียวกันจะสร้างน้ำหนักเท่ากัน

- ประสิทธิภาพ หน่วยความจำ: รองรับความแม่นยำ float16 เพื่อลดการใช้หน่วยความจำวิดีโอ

1.3 การสร้างเวกเตอร์เป้าหมายและการคำนวณระยะทาง

เวกเตอร์เป้าหมายมีการกระจายอย่างสม่ำเสมอบนทรงกลมหน่วยมิติสูง ซึ่งเป็นกุญแจสำคัญต่อความยุติธรรมของโจทย์การคำนวณ การสร้างเวกเตอร์เป้าหมายที่มีการกระจายอย่างสม่ำเสมอในพื้นที่มิติสูง ช่วยให้มั่นใจได้ถึงความสุ่มและความยุติธรรมของโจทย์การคำนวณ

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/random.py#L165-L177

ในพื้นที่คำศัพท์ขนาด 4096 มิติ เรขาคณิตทรงกลมมีคุณสมบัติต่อไปนี้:

- ความยาวหน่วย :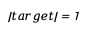

- การกระจาย มุม: มุมระหว่างเวกเตอร์สุ่มสองตัวใดๆ มีแนวโน้มเป็น 90°

- ปรากฏการณ์การรวมตัว : มวลส่วนใหญ่กระจายตัวใกล้ผิวทรงกลม

หลักคณิตศาสตร์ของการกระจายสม่ำเสมอบนทรงกลม:

ในปริภูมิ n มิติ สามารถสร้างการกระจายแบบสม่ำเสมอบนทรงกลมหน่วยได้ดังนี้:

1. สร้างตัวแปรสุ่มการแจกแจงแบบปกติมาตรฐานอิสระจำนวน n ตัวก่อน: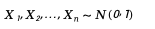

2. จากนั้นทำให้เป็นปกติ: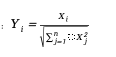

วิธีนี้ช่วยให้แน่ใจว่าเวกเตอร์ที่สร้างขึ้นจะกระจายอย่างสม่ำเสมอบนทรงกลม และนิพจน์ทางคณิตศาสตร์คือ:

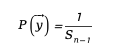
ใน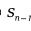 คือพื้นที่ผิวของทรงกลม n-1

การคำนวณระยะทางเป็นขั้นตอนสำคัญในการตรวจสอบผลการคำนวณ ประสิทธิภาพของการคำนวณวัดโดยการคำนวณระยะทางแบบยุคลิดระหว่างผลลัพธ์ของแบบจำลองและเวกเตอร์เป้าหมาย:

แหล่งที่มาของข้อมูล : อ้างอิงจากตรรกะการประมวลผลใน mlnode/packages/pow/src/pow/compute/compute.py

ขั้นตอนการคำนวณระยะทาง:

1. การประยุกต์ใช้การเรียงสับเปลี่ยน : จัดเรียงมิติผลลัพธ์ใหม่ตามค่าเมล็ดพันธุ์การเรียงสับเปลี่ยน

2. การทำให้เวกเตอร์เป็นมาตรฐาน : ตรวจสอบให้แน่ใจว่าเวกเตอร์เอาต์พุตทั้งหมดอยู่บนทรงกลมหน่วย

3. การคำนวณระยะทาง : คำนวณระยะทางแบบยุคลิดไปยังเวกเตอร์เป้าหมาย

4. การห่อหุ้มแบบแบตช์ : ห่อหุ้มผลลัพธ์ไว้ในโครงสร้างข้อมูล ProofBatch

2. กลไกการตรวจสอบป้องกันการโกง

เพื่อให้มั่นใจถึงความยุติธรรมและความปลอดภัยของความท้าทายในการคำนวณ ระบบจึงได้ออกแบบระบบตรวจสอบป้องกันการโกงที่ซับซ้อน กลไกนี้จะตรวจสอบความถูกต้องของการคำนวณผ่านการสุ่มตัวอย่างแบบกำหนดและการทดสอบทางสถิติ เพื่อป้องกันไม่ให้โหนดที่เป็นอันตรายได้รับประโยชน์ที่ไม่เหมาะสมจากการโกง

2.1 โครงสร้างข้อมูล ProofBatch

ผลการคำนวณจะถูกรวมไว้ในโครงสร้างข้อมูล ProofBatch ซึ่งเป็นแกนหลักของกระบวนการตรวจสอบ ProofBatch ประกอบด้วยข้อมูลประจำตัวของโหนดประมวลผล ประทับเวลา และผลการคำนวณ ซึ่งเป็นพื้นฐานข้อมูลที่จำเป็นสำหรับการตรวจสอบในภายหลัง

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/data.py#L8-L25

ลักษณะเฉพาะของโครงสร้างข้อมูล ProofBatch:

-Identity : public_key ระบุโหนดการประมวลผลอย่างเฉพาะเจาะจง

- การผูกบล็อคเชน : block_hash และ block_height ช่วยให้การซิงโครไนซ์เวลาเป็นไปได้

-ผลการคำนวณ : บันทึก nonces และ dist ความพยายามทั้งหมดและค่าระยะทาง

- การสนับสนุนชุดย่อย : รองรับการแยกการคำนวณที่ประสบความสำเร็จที่ตรงตามเกณฑ์

2.2 กลไกการสุ่มตัวอย่างแบบกำหนด

เพื่อเพิ่มประสิทธิภาพในการตรวจสอบ ระบบจึงใช้กลไกการสุ่มตัวอย่างแบบกำหนด (deterministic sampling) โดยตรวจสอบเฉพาะผลการคำนวณบางส่วนเท่านั้น แทนที่จะตรวจสอบทั้งหมด การออกแบบนี้ไม่เพียงแต่รับประกันประสิทธิภาพในการตรวจสอบเท่านั้น แต่ยังช่วยลดต้นทุนในการตรวจสอบได้อย่างมากอีกด้วย

อัตราการสุ่มตัวอย่างเพื่อการยืนยันของ Gonka ได้รับการจัดการอย่างสม่ำเสมอผ่านพารามิเตอร์บนเชนเพื่อให้แน่ใจว่ามีความสอดคล้องกันทั่วทั้งเครือข่าย:

แหล่งที่มาของข้อมูล : inference-chain/proto/inference/inference/params.proto#L75-L78

แหล่งที่มาของข้อมูล : inference-chain/x/inference/types/params.go#L129-L133

กระบวนการสุ่มตัวอย่างเป็นระบบกำหนดตายตัวอย่างสมบูรณ์ โดยยึดตามระบบ Seed เพื่อให้แน่ใจว่าการตรวจสอบมีความยุติธรรม ด้วยการใช้ฟังก์ชันแฮช SHA-256 และคีย์สาธารณะของตัวตรวจสอบ แฮชบล็อก ความสูงของบล็อก และข้อมูลอื่นๆ เพื่อสร้าง Seed ผู้ตรวจสอบทั้งหมดจึงมั่นใจได้ว่าจะใช้กลยุทธ์การสุ่มตัวอย่างแบบเดียวกัน:

แหล่งที่มาของข้อมูล : decentralized-api/mlnodeclient/poc.go#L175-L201

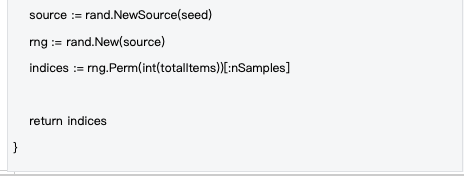
ข้อดีของการสุ่มตัวอย่างแบบกำหนด:

- ความยุติธรรม : ผู้ตรวจสอบทั้งหมดใช้กลยุทธ์การสุ่มตัวอย่างแบบเดียวกัน

- ประสิทธิภาพ : ตรวจสอบข้อมูลเพียงบางส่วนเพื่อลดต้นทุนการตรวจสอบ

- ความปลอดภัย : ยากที่จะคาดเดาข้อมูลตัวอย่างเพื่อป้องกันการโกง

2.3 การตรวจจับการฉ้อโกงทางสถิติ

ระบบใช้การทดสอบการแจกแจงแบบทวินามเพื่อตรวจจับการฉ้อโกง โดยใช้วิธีการทางสถิติเพื่อประเมินความถูกต้องของโหนดการประมวลผล วิธีการนี้จะกำหนดอัตราความผิดพลาดที่คาดไว้โดยพิจารณาจากความแม่นยำของฮาร์ดแวร์และความซับซ้อนในการคำนวณ และใช้การทดสอบทางสถิติเพื่อตรวจจับความผิดปกติ

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/data.py#L7

อัตราข้อผิดพลาดที่คาดหวังจะถูกกำหนดโดยคำนึงถึงปัจจัยต่อไปนี้:

- ความแม่นยำของจุด ลอยตัว: ความแตกต่างในความแม่นยำของจุดลอยตัวระหว่างฮาร์ดแวร์ที่แตกต่างกัน

- การคำนวณแบบขนาน : ข้อผิดพลาดในการสะสมตัวเลขที่เกิดจากการประมวลผลแบบขนานของ GPU

- ความสุ่ม : ความแตกต่างเล็กน้อยในการเริ่มต้นน้ำหนักของโมเดล

- ความแตกต่างของ ระบบ: ความแตกต่างของพฤติกรรมการประมวลผลระหว่างระบบปฏิบัติการและไดรเวอร์ที่แตกต่างกัน

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/data.py#L174-L204

สรุป: การสร้างเครือข่ายคอมพิวเตอร์ AI ที่ปลอดภัยและเชื่อถือได้

Gonka PoW 2.0 ประสบความสำเร็จในการผสานรวมข้อกำหนดด้านความปลอดภัยของบล็อกเชนเข้ากับคุณค่าเชิงปฏิบัติของการประมวลผลด้วย AI ผ่านกลไกการตรวจสอบและป้องกันการโกงที่ออกแบบมาอย่างพิถีพิถัน กลไกการตรวจสอบและป้องกันการโกงนี้ช่วยรับประกันถึงความหมายของงาน ขณะที่กลไกป้องกันการโกงช่วยรับประกันความยุติธรรมและความปลอดภัยของเครือข่าย

การออกแบบนี้ไม่เพียงแต่ตรวจสอบความเป็นไปได้ทางเทคนิคของ "การขุดที่มีความหมาย" เท่านั้น แต่ยังสร้างมาตรฐานใหม่สำหรับการประมวลผล AI แบบกระจายอีกด้วย: การประมวลผลจะต้องมีความปลอดภัยและเป็นประโยชน์ สามารถตรวจสอบได้และมีประสิทธิภาพ

ด้วยการผสมผสานสถิติ การเข้ารหัส และการออกแบบระบบแบบกระจาย Gonka PoW 2.0 ประสบความสำเร็จในการสร้างกลไกป้องกันการโกงที่เชื่อถือได้ ขณะเดียวกันก็รับประกันประโยชน์ในการคำนวณ พร้อมทั้งให้รากฐานความปลอดภัยที่มั่นคงสำหรับเส้นทางทางเทคนิคของ "การขุดที่มีความหมาย"

หมายเหตุ: บทความนี้อ้างอิงจากการใช้งานโค้ดจริงและเอกสารประกอบการออกแบบของโครงการ Gonka การวิเคราะห์ทางเทคนิคและพารามิเตอร์การกำหนดค่าทั้งหมดมาจากคลังโค้ดอย่างเป็นทางการของโครงการ

เกี่ยวกับ Gonka.ai

Gonka คือเครือข่ายแบบกระจายศูนย์ที่ออกแบบมาเพื่อมอบพลังการประมวลผล AI ที่มีประสิทธิภาพ เป้าหมายการออกแบบคือการเพิ่มประสิทธิภาพการใช้พลังการประมวลผล GPU ทั่วโลกให้สูงสุดเพื่อจัดการเวิร์กโหลด AI ที่สำคัญ ด้วยการขจัดระบบเกตเวย์แบบรวมศูนย์ Gonka จึงช่วยให้นักพัฒนาและนักวิจัยเข้าถึงทรัพยากรการประมวลผลได้โดยไม่ต้องขออนุญาต ขณะเดียวกันก็มอบโทเค็น GNK ดั้งเดิมให้กับผู้เข้าร่วมทุกคน

Gonka ได้รับการบ่มเพาะโดย Product Science Inc. ผู้พัฒนา AI สัญชาติอเมริกัน ก่อตั้งโดยพี่น้องตระกูล Liberman ผู้คร่ำหวอดในวงการ Web 2 และอดีตผู้อำนวยการฝ่ายผลิตภัณฑ์หลักของ Snap Inc. บริษัทประสบความสำเร็จในการระดมทุน 18 ล้านดอลลาร์ในปี 2023 จากนักลงทุน ได้แก่ Coatue Management ซึ่งเป็นนักลงทุนใน OpenAI, Slow Ventures ซึ่งเป็นนักลงทุนใน Solana, K5, Insight และ Benchmark Partners ผู้ร่วมก่อตั้งโครงการในช่วงแรก ๆ ได้แก่ ผู้นำที่มีชื่อเสียงในวงการ Web 2-Web 3 เช่น 6 Blocks, Hard Yaka, Gcore และ Bitfury

เว็บไซต์อย่างเป็นทางการ | Github | X | Discord | เอกสารเผยแพร่ | แบบจำลองเศรษฐกิจ | คู่มือผู้ใช้