ต่อจากบทที่แล้ว เราได้เผยแพร่บทความสี่บทความในชุดบทความเกี่ยวกับ การสร้างพอร์ตโฟลิโอสินทรัพย์ดิจิทัลที่มีประสิทธิภาพโดยใช้แบบจำลองหลายปัจจัย:“พื้นฐานทางทฤษฎี”、“การประมวลผลข้อมูลล่วงหน้า”、การทดสอบความถูกต้องของปัจจัย、การวิเคราะห์ปัจจัยประเภทใหญ่: การสังเคราะห์ปัจจัย。

ในบทความก่อนหน้านี้ เราได้อธิบายโดยละเอียดเกี่ยวกับปัญหาของปัจจัยที่เชื่อมโยงกัน (ความสัมพันธ์สูงระหว่างปัจจัยต่างๆ) ก่อนที่จะสังเคราะห์ปัจจัยประเภทใหญ่ๆ จำเป็นต้องดำเนินการปรับมุมฉากของปัจจัยเพื่อกำจัดความไม่สอดคล้องกัน

1. การได้มาทางคณิตศาสตร์ของปัจจัยตั้งฉาก

จากมุมมองของการถดถอยภาคตัดขวางแบบหลายปัจจัย ระบบปัจจัยตั้งฉากได้ถูกสร้างขึ้น

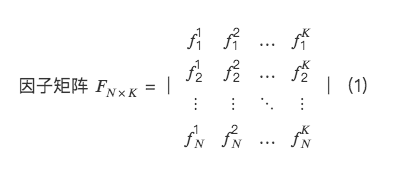
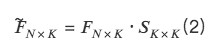
ดังนั้น,

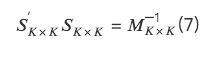
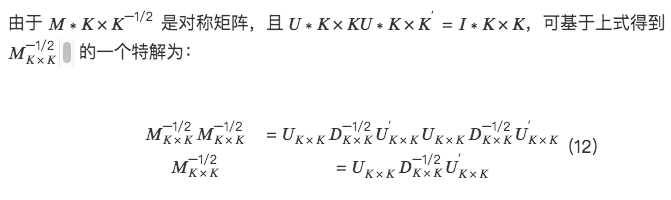
2. การใช้งานเฉพาะของวิธีการตั้งฉากสามวิธี

1.ชมิตต์ตั้งฉาก

Schmidt orthogonal เป็นวิธีการแบบ sequential orthogonal ดังนั้นจึงจำเป็นต้องกำหนดลำดับของปัจจัย orthogonality ลำดับ orthogonal ทั่วไปรวมถึงลำดับคงที่ (ลำดับ orthogonal เดียวกันจะใช้ในส่วนที่แตกต่างกัน) และลำดับแบบไดนามิก (ลำดับ orthogonal เดียวกันถูกนำมาใช้ในแต่ละส่วน) มาตรา) ลำดับมุมฉากถูกกำหนดตามกฎบางประการ) ข้อดีของวิธีตั้งฉากของชมิดต์คือมีความสอดคล้องกันอย่างชัดเจนระหว่างปัจจัยตั้งฉากในลำดับเดียวกัน อย่างไรก็ตาม ไม่มีมาตรฐานการเลือกแบบรวมสำหรับลำดับมุมฉาก ประสิทธิภาพหลังการจัดมุมฉากอาจได้รับผลกระทบจากมาตรฐานลำดับมุมฉากและระยะเวลาของหน้าต่าง พารามิเตอร์ .

2. ความตั้งฉากปกติ

# Canonical orthogonal def Canonical(ตนเอง):
 overlapping_matrix = (time_tag_data.shape[ 1 ] - 1) * np.cov(time_tag_data.astype(float))
# รับค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะ
 eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix)
# แปลงเป็นเมทริกซ์ใน np
 eigenvector = np.mat(eigenvector)
 transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5))))
 orthogonalization = np.dot(time_tag_data.T.values, transition_matrix)
 orthogonalization_df = pd.DataFrame(orthogonalization.T, index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]), columns=time_tag_data.columns)
 self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)

3. มุมฉากสมมาตร

เนื่องจาก Schmidt orthogonal ใช้ลำดับมุมฉากเดียวกันของปัจจัยในหลายส่วนที่ผ่านมา จึงมีความสอดคล้องกันอย่างชัดเจนระหว่างปัจจัย orthogonal และปัจจัยดั้งเดิม ในขณะที่ canonical orthogonal เลือกส่วนประกอบหลักในแต่ละส่วน ทิศทางอาจไม่สอดคล้องกัน ส่งผลให้ไม่มี ความสอดคล้องที่มั่นคงระหว่างปัจจัยก่อนและหลัง orthogonality จะเห็นได้ว่าผลของการรวมมุมฉากนั้นขึ้นอยู่กับว่ามีความสอดคล้องกันอย่างมั่นคงระหว่างปัจจัยก่อนและหลังความเป็นมุมฉากหรือไม่

ความตั้งฉากแบบสมมาตรช่วยลดการปรับเปลี่ยนเมทริกซ์แฟกเตอร์ดั้งเดิมให้มากที่สุดเท่าที่จะเป็นไปได้เพื่อให้ได้ชุดของฐานตั้งฉาก สิ่งนี้สามารถรักษาความคล้ายคลึงกันระหว่างปัจจัยตั้งฉากและปัจจัยเชิงสาเหตุได้ในระดับสูงสุด และหลีกเลี่ยงปัจจัยที่เอื้ออำนวยตั้งแต่ต้นในลำดับตั้งฉาก เช่น วิธีตั้งฉากของชมิดท์

คุณสมบัติมุมฉากสมมาตร:

1. เมื่อเปรียบเทียบกับ Schmidt orthogonal แล้ว Symmetric orthogonal ไม่จำเป็นต้องจัดลำดับ orthogonal และปฏิบัติต่อแต่ละปัจจัยอย่างเท่าเทียมกัน

2. ในบรรดาเมทริกซ์การเปลี่ยนฉากมุมฉากทั้งหมด ความคล้ายคลึงกันระหว่างเมทริกซ์มุมฉากสมมาตรและเมทริกซ์ดั้งเดิมนั้นยิ่งใหญ่ที่สุด นั่นคือระยะห่างระหว่างเมทริกซ์ก่อนและหลังเมทริกซ์มุมฉากนั้นเล็กที่สุด