กลุ่มโบนัสการวิจัย DAOrayaki DAO:

ที่อยู่ของทุน: DAOrayaki.eth

กลุ่มโบนัสการวิจัย DAOrayaki DAO:

ที่อยู่ของทุน: DAOrayaki.eth

ความคืบหน้าการลงคะแนน คณะกรรมการ กพท. ผ่านไปแล้ว 2/0

ประเภทการวิจัย: Blockchain Zero Knowledge Proofs

zkSNARKs เป็นวิธีสร้างการพิสูจน์ที่ไม่มีความรู้ โดยเฉพาะอย่างยิ่ง วิธีการที่รัดกุมและไม่โต้ตอบสำหรับการสร้างการพิสูจน์ที่ไม่มีความรู้

ผู้เขียนต้นฉบับ: Kobi Gurkan

zkSNARKs เป็นวิธีสร้างการพิสูจน์ที่ไม่มีความรู้ โดยเฉพาะอย่างยิ่ง วิธีการที่รัดกุมและไม่โต้ตอบสำหรับการสร้างการพิสูจน์ที่ไม่มีความรู้

https://z.cash/technology/zksnarks/

zkSNARKs คืออะไร สามารถอ้างอิงได้ดังต่อไปนี้

1. วิธีสร้าง zkSNARK ใน Zcash - เอื้อเฟื้อโดยทีมงาน Zcash

https://qed-it.com/trustless-computing-on-private-data/

2. การประมวลผลที่ไม่น่าเชื่อถือสำหรับข้อมูลส่วนตัว - Daniel Benarroch และ Aviv Zohar หัวหน้านักเข้ารหัสที่ QED-it

โพสต์บล็อกของศาสตราจารย์

https://qed-it.com/2017/07/04/zkp-in-action/

3. หลักฐาน บล็อกเชน ZKPinAction - เซสชันที่อธิบาย ZKP และวิธีการสร้าง ZKP สำหรับ Sudoku

https://qed-it.com/2017-12-20-the-incredible-machine/

วิดีโอ

https://qed-it.com/2017/07/11/the-hunting-of-the-snark/

4. The Incredible Machine - บล็อกโพสต์โดย Prof. Aviv Zohar หัวหน้านักวิทยาศาสตร์ของ QED-it อธิบายการตั้งค่าที่เชื่อได้

5. การล่าสัตว์ SNARK - ชุดปริศนาสำหรับการทดลองกับ ZKP

ที่ QED-it เราใช้ zkSNARK และเครื่องมืออื่นๆ เพื่อสร้างบล็อกเชนที่ไม่มีความรู้สำหรับองค์กร

การปรับใช้การผลิตที่เป็นที่รู้จักดีที่สุดของ zkSNARKs น่าจะเป็น ZCash ซึ่งเป็นสกุลเงินดิจิทัลที่มีธุรกรรมที่ไม่สามารถเชื่อมโยงได้และจำนวนเงินที่ซ่อนอยู่ ZCash รวมถึงผลิตภัณฑ์อื่นๆ ที่ใช้ zkSNARK นั้นใช้โครงสร้างที่เรียกว่า Pinnochio แม้ว่าจะเป็น BCTV14a อย่างเจาะจงกว่านั้นก็ตาม เป็นเทคโนโลยีที่น่าทึ่งอย่างที่คุณอาจสงสัย โครงสร้างนี้มีข้อเสียที่ชัดเจน: การตั้งค่าที่เชื่อถือได้"การตั้งค่าที่เชื่อถือได้"การตั้งค่าคือกระบวนการสร้าง CRS (Common Reference String) หรือที่เรียกกันทั่วไปว่าคู่ของคีย์ใบรับรองและการตรวจสอบยืนยัน เหล่านี้

สำคัญ"ผู้พิสูจน์และผู้ตรวจสอบจะใช้เพื่อสร้างและตรวจสอบหลักฐานของปัญหาเฉพาะ (หรือระบบข้อจำกัด) ตามลำดับ"ในระหว่างขั้นตอนนี้ องค์ประกอบสุ่มบางส่วนจะถูกสุ่มตัวอย่างแต่ต้องเก็บเป็นความลับ เนื่องจากหากผู้ตรวจสอบรู้เรื่องนี้ พวกเขาจะสามารถสร้างการพิสูจน์ที่ตรวจสอบได้สำเร็จโดยไม่ต้องใช้วิธีแก้ปัญหาจริงในกระบวนการพิสูจน์ กล่าวอีกนัยหนึ่งเพื่อปลอมแปลงหลักฐานและบ่อนทำลายความถูกต้อง การสุ่มนี้เรียกอีกอย่างว่า

. มีวิธีหลีกเลี่ยงข้อกังวลนี้โดยการไม่ไว้วางใจในหน่วยงานเดียว สำหรับวงจรสาธารณะ วิธีการเหล่านี้มักเกี่ยวข้องกับการคำนวณแบบหลายฝ่าย ซึ่งผู้เข้าร่วมหลายคนบริจาคการสุ่ม ซึ่งต่อมาจะถูกทำลายไป ที่น่าสนใจคือ ตราบใดที่ผู้เข้าร่วมคนหนึ่งมีความซื่อสัตย์และความสุ่มเสี่ยงของพวกเขาถูกทำลาย กระบวนการทั้งหมดก็จะปลอดภัย

1. "The Ceremony "พอดคาสต์

https://www.wnycstudios.org/podcasts/radiolab/articles/ceremony

ตัวอย่างที่โดดเด่นของการตั้งค่าที่เชื่อถือได้โดยใช้ MPC ยังคงอยู่: ZCash

https://z.cash.foundation/blog/powers-of-tau/

พอดคาสต์"Tau"2. พลังแห่งเอกภาพ

คุณอาจสังเกตเห็นสิ่งนี้ปรากฏขึ้นที่นี่

...ความลับของเทานั้นสำคัญมาก เมื่อ Tau รู้จักกับผู้พิสูจน์แล้ว การปลอมแปลงหลักฐานจึงเป็นเรื่องง่าย

สร้างใบรับรอง

มาดูการก่อสร้างที่เสนอใน BCTV14a กัน"นี่เป็นปัญหาทางคณิตศาสตร์ ดังนั้นเรามาดูรายละเอียดที่เกี่ยวข้องกับบทความนี้กัน:"1. Tau คือจุดในฟิลด์จำกัดที่วาดแบบสุ่มระหว่างการตั้งค่าและเป็น

ของเสียที่เป็นพิษ"a*b=c "ส่วนหนึ่งของมัน"a*b-c=0"。

2. ระหว่างการพิสูจน์ ผู้ตรวจสอบจะคำนวณพหุนาม - A(z), B(z) และ C(z) จากคำตอบของระบบข้อจำกัดและอินพุตสาธารณะและส่วนตัว โดยพื้นฐานแล้ว พหุนามเหล่านี้เป็นตัวแทน"ข้อจำกัดของรูปแบบหรือเทียบเท่า"H(z)--H(Tau)。

3. ตัวตรวจสอบยังคำนวณ H(z)=(A(z)B(z)-C(z))/Z(z) โดยที่ Z(z) เป็นพหุนามสาธารณะที่จุดที่เป็นตัวแทนของระบบข้อจำกัดเป็นศูนย์ โปรดทราบว่าเนื่องจาก A, B และ C คำนึงถึงอินพุตของผู้ตรวจสอบ ดังนั้น H จึงจะสามารถคำนวณได้ก็ต่อเมื่อตัวเศษเป็นศูนย์ที่จุดเดียวกันเท่านั้น เป็นการพิสูจน์ว่าผู้ตรวจสอบทราบวิธีแก้ปัญหาที่ให้ A*BC =0 . ตอนนี้ส่วนสำคัญเกิดขึ้น - โดยไม่รู้ว่า Tau ผู้ตรวจสอบสามารถคำนวณได้

ภายในดัชนี

ทำไมเราทำเช่นนี้? เนื่องจากการประเมินที่จุดสุ่ม Tau ผู้พิสูจน์มีความเป็นไปได้สูงที่จะแสดงว่าสมการ H=(A*BC)/Z ถือ Z ทั้งหมด จากมุมมองที่แตกต่างกันเกี่ยวกับปัญหาเดียวกัน โดยไม่รู้ว่า Tau ผู้พิสูจน์ซึ่งมีความเป็นไปได้สูง จะไม่สามารถสร้างพหุนามที่ให้ค่าเดียวกันได้ ณ จุดนั้น

เราจะทำอย่างไรในทางเทคนิค? มีความจริงที่ว่าส่วนหนึ่งของขั้นตอนการตั้งค่าสร้างองค์ประกอบที่มีกำลังที่เกี่ยวข้องทั้งหมดของ Tau ซ่อนอยู่ในเลขยกกำลัง โดยกำหนดเป็น pk_Hi ถ้าเรามีค่าสัมประสิทธิ์ของ H เราสามารถรวมค่าเหล่านี้เข้าด้วยกันและสร้าง H(Tau)

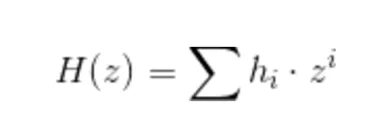
โดยเฉพาะอย่างยิ่ง

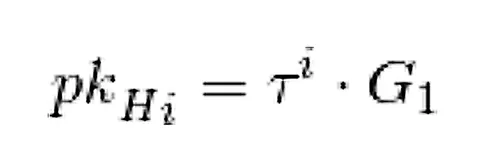
H(z) คำนวณโดยผู้ตรวจสอบ

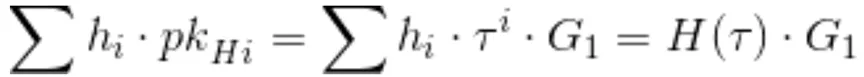
คีย์ที่นำมาจากการรับรอง คำนวณระหว่างการตั้งค่า

การประเมิน "ภายในเอกซ์โพเนนเชียล" ของ H (เอกภาพ)

หลังจากได้รับการพิสูจน์แล้ว ผู้ตรวจสอบสามารถตรวจสอบอีกครั้งในเลขยกกำลังว่าผู้ตรวจสอบได้ระบุค่าสัมประสิทธิ์ของ H ที่ตรงตามความสัมพันธ์ H=(A*BC)/Z หรือไม่ ซึ่งจะทำได้ก็ต่อเมื่อผู้ตรวจสอบทราบวิธีแก้ปัญหาจริงๆ เท่านั้น

ใบรับรองปลอม

ทีนี้มาตั้งสมมุติฐานกันว่าถ้ารู้จัก Tau จะเป็นอย่างไร? หากมีการเปิดเผยในระหว่างการตั้งค่าด้วยเหตุผลบางอย่างและทราบโดยโปรแกรมตรวจสอบที่เป็นอันตราย

เห็นได้ชัดว่ามันง่ายมากที่จะปลอมแปลงหลักฐาน เนื่องจากการตรวจสอบความสมมูลสำหรับ H=(A*BC)/Z เสร็จสิ้นที่จุดเฉพาะของ Tau เราจึงสามารถใช้สิ่งที่เรารู้เกี่ยวกับ Tau เพื่อสร้างพหุนามที่ตอบสนองได้อย่างเต็มที่ นั่นคือ สร้างพหุนามคงที่ H(z) ซึ่งจะคืนค่า (A(Tau)*B(Tau)-C(Tau))/Z(Tau) เสมอ

การตรวจสอบของผู้ตรวจสอบจะผ่านไปและไม่มีใครรู้ ฟังดูยาก...

ไม่เลย. คุณยินดีอย่างยิ่งที่จะตรวจสอบรหัสพิสูจน์แนวคิดนี้ ซึ่งอ้างอิงจาก libsnarktutorial ของ Howard Wu และดูการเปลี่ยนแปลงที่เกิดขึ้นกับรหัสด้วยตัวคุณเอง

1. โปรแกรมตั้งค่าวงจรสำหรับการแยกบิตแม้ว่าจะเป็น C

3. ตัวตรวจสอบโหลด Tau จากดิสก์และพิสูจน์ด้วยการป้อนข้อมูลที่ไม่ถูกต้อง ผู้ตรวจสอบซึ่งรู้จัก Tau จะสร้างพหุนามคงที่โดยไม่คำนึงถึงอินพุต

สรุปแล้ว

จากนั้นผู้ตรวจสอบจะตรวจสอบหลักฐานสำเร็จ!"สรุปแล้ว"ฉันหวังว่าโพสต์นี้จะให้ข้อมูลเชิงลึกเกี่ยวกับสิ่งที่ทุกคนพูดถึงเกี่ยวกับ zkSNARK