B² Network技术实现:基于零知识证明验证承诺的比特币ZK-Rollup
原文作者:Stone, B² Network Research Lead
B² Network 是比特幣上的一個Layer 2 解決方案,主要利用將零知識證明驗證承諾提交到比特幣網絡,允許挑戰者發起欺詐證明進行挑戰,以達到利用比特幣網絡的強大共識保證B² Network 安全性的目的。
本文主要介紹以太坊上的ZK-Rollup 和OP-Rollup 的運作機制,介紹神奇的與非閘電路,介紹承諾的作用,並利用這些機制和概念設計B² Network 上的零知識證明驗證承諾,進而說明零知識證明驗證承諾如何在比特幣網絡執行以及如何保證B² Network 的安全性。
以太坊上的ZK-Rollup
ZK-Rollup 是一種區塊鏈的二層擴展解決方案,透過聚合多個交易並利用零知識證明來確保這些交易批次的正確性和完整性,並在一層區塊鍊網絡上進行零知識證明的驗證,從而利用一層網絡來確保二層網絡的安全性。它旨在提高區塊鏈系統的吞吐量,減少交易費用,同時保持高度的安全性和資料完整性。
ZK-Rollup 的運作過程大致如下:
交易聚合和排序。用戶向ZK-Rollup 提交交易,交易將會提交到mempool 中。 ZK-Rollup 的Sequencer 從mempool 中獲取使用者的交易並進行收集、排序,Sequencer 負責處理交易,更新帳戶狀態,並最終產生一個代表這些更新的批次;
狀態轉換和計算。所有的交易執行和狀態更新都在鏈下進行。 ZK-Rollup 的VM(包括zkEVM、zkVM 等不同的零知識證明智慧合約執行引擎)計算新的帳戶狀態,並處理如轉帳、智慧合約互動等作業。同時產生必要的數據和證據來證明這些交易和狀態更新是有效的,這裡麵包括新的帳戶狀態和零知識證明;
零知識證明生成。 ZK-Rollup 的Prover 利用零知識證明技術(如zk-SNARKs 或zk-STARKs)來創建一個證明,這個證明表明所有聚合的交易都是有效的,沒有違反網絡規則。這個證明不透露任何有關交易內容的信息,保護用戶隱私,同時確保了資料的完整性和安全性。
零知識證明驗證。 Aggregator 將批次的數據和零知識證明提交到一層區塊鍊網絡。這通常以一種壓縮的形式發生,以減少所需的鏈上空間。一層區塊鍊網路上的智慧合約接收這些數據和證明,並驗證證明的有效性。如果證明有效,合約將更新其記錄的ZK-Rollup 層的狀態。
ZK-Rollup 的核心在於零知識證明的產生與驗證。 ZK-Rollup 的交易在鏈下執行,並在鏈下產生狀態,透過Prover 產生零知識證明,作為ZK-Rollup 的承諾。這個承諾代表著ZK-Rollup 上的交易正確、有效地執行,產生了正確的狀態。一層區塊鍊網絡不需要驗證ZK-Rollup 的全部交易和狀態,只需要驗證承諾,承諾的驗證是透過一層網路的智慧合約進行零知識證明驗證,即可確認ZK-Rollup 的有效性。
因此,在以太坊的ZK-Rollup 中,零知識證明資料是二層網路向一層網路提交的承諾。
以太坊上的OP-Rollup
Optimistic Rollup (OP-Rollup) 是一種為了擴展區塊鏈效能而設計的技術,它透過在鏈上保持最小的數據和執行盡可能多的計算在鏈下來實現。 OP-Rollup 利用了「樂觀」假設,即大部分交易都是誠實的,而不是立即驗證每個交易的有效性,這樣可以在一段時間後再進行驗證,大大提高了吞吐量和效率。
OP-Rollup 的運作過程大致如下:
交易聚合和排序。用戶向OP-Rollup 提交交易,交易將會提交到mempool 中。 OP-Rollup 的Sequencer 從mempool 中獲取使用者的交易並進行收集、排序,Sequencer 負責處理交易,更新帳戶狀態,並最終產生一個代表這些更新的批次;
交易的執行。 OP-Rollup 的交易在鏈下執行,每個批次交易的執行,將導致舊的狀態轉變為新的狀態,每個批次都會計算一個新的狀態根(一種加密的“快照”表示整個系統狀態),並將其提交到一層區塊鍊網絡;
狀態的驗證。 OP-Rollup 在提交交易批次時不立即進行複雜的驗證,而是「樂觀地」假設這些交易都是有效的,然後提交一層區塊鍊網絡。如果有觀察者認為某個批次是無效的,他們可以提交一個欺詐證明來挑戰該批次。在Optimistic Rollup 解決方案中,詐騙證明是一種允許任何觀察者挑戰錯誤或惡意提交到鏈上的狀態或交易的機制。 Optimistic Rollup 利用詐騙證明來確保即使是「樂觀地」接受的交易也可以在事後被證明是錯誤的,並相應地被撤銷;
挑戰機制。挑戰期是OP-Rollup 提交狀態確認後,有一個挑戰窗口期,期間任何人都可以檢查提交的批次,並在發現錯誤時提交欺詐證明,這通常是通過提交一個交易到一層區塊鍊網路來實現,該交易聲明了他們認為的錯誤並提供了相應的證據。 Arbitrum Rollup(一種Optimistic Rollup 的解決方案)使用稱為「互動式驗證遊戲」的流程來解決挑戰。在這個過程中,挑戰者和提交者之間進行一系列的回合,逐步縮小他們對哪裡出錯的意見不一致的範圍(採用的是二分查找法快速定位錯誤的交易位置)。最終,這個過程將確定錯誤發生的確切位置。一旦錯誤被確認,原始的批次將被撤銷,並對提出錯誤的驗證者進行處罰。如果挑戰失敗,挑戰者可能會失去他們為發起挑戰而抵押的資金;如果挑戰成功,則挑戰者可以獲得成功發起挑戰贏得的獎勵資金。
OP-Rollup 的核心在於詐騙證明和挑戰機制。 OP-Rollup 首先會「樂觀」地認為所有交易都正確執行,然後在一層網絡將計算編譯為合約內虛擬機(AVM、OVM)的字節碼,發布字節碼的承諾。 OP-Rollup 的承諾驗證,需要進行交易計算,並獲得字節碼,然後驗證承諾。一旦有觀察者發現有承諾不匹配的批次,觀察者將通過挑戰機制產生詐騙證明,獲得獎勵。
以太坊的OP-Rollup 首先「樂觀」地確認和提交承諾,然後利用挑戰機制,允許任何人對提交的承諾進行挑戰,最終通過承諾和挑戰確保OP-Rollup 得到驗證和確認。
神奇的與非門
與非閘(NAND gate)是數字邏輯中的一種基本邏輯閘,它實現了邏輯與(AND)運算後的邏輯非(NOT)運算。與非閘的特性使其成為能夠建構任何其他邏輯閘和複雜邏輯電路的基礎。以下是如何使用與非閘構造邏輯閘(如與閘、或閘、異或閘)以及加法閘與減法閘的詳細介紹:
1. 與非門基礎
與非閘有兩個輸入,當且僅當兩個輸入都為1 時,輸出為0 ;在所有其他情況下,輸出為1 。這可以用邏輯表達式表示為A NAND B。
2. 建構基本邏輯閘
與門(AND)
要使用與非門構造與門:
第一步:將兩個輸入連接到一個與非閘。
第二步:將該與非閘的輸出連接到另一個與非閘的兩個輸入端。
結果:第二個與非閘的輸出就是與閘的結果。
或門(OR)
要使用與非門構造或門:
第一步:將每個輸入分別通過一個與非閘(自己與自己),產生兩個非閘的效果。
第二步:將這兩個與非閘的輸出作為一個與非閘的輸入。
結果:該與非閘的輸出就是或閘的結果。
異或門(XOR)
要使用與非門構造異或門(更複雜一些):
第一步:建構兩個與非閘,每個輸入都連接到其中一個。
第二步:將第一步驟中的兩個與非閘的輸出作為第三個與非閘的輸入。
第三步:將原始輸入A 和第一個與非閘的輸出連接到第四個與非閘,將原始輸入B 和第二個與非閘的輸出連接到第五個與非閘。
第四步:最後,將第四個與第五個與非閘的輸出連接到第六個與非閘。
結果:第六個與非閘的輸出就是異或閘的結果。
3. 構造加法門
半加法器(Half Adder)
半加法器是一個簡單的加法器,它可以處理兩個位元的加法,並產生和(sum)和進位(carry)。
和:使用一個異或門來產生和。
進位:使用一個與閘來產生進位。
使用與非門構造這些基本門,然後將它們組合起來形成半加法器。
全加器(Full Adder)
全加器考慮了來自低位的進位輸入。
第一步:建構兩個半加法器,第一個處理A 和B,第二個處理第一個半加法器的和與進位輸入C。
和:第二個半加法器的和輸出。
進位:兩個半加法器的進位輸出透過一個或閘連接。
使用與非門構造半加法器和或門,然後組合它們形成全加法器。
4. 構造減法門
半減器(Half Subtractor)
半減器處理兩個位元的減法。
差:使用一個異或門生成差。
借位:使用一個與非門和非門來產生借位。
使用與非閘構造異或閘和其他所需邏輯,然後組合它們形成半減器。
全減器(Full Subtractor)
全減器考慮了來自高位的借位。
第一步:建構兩個半減器,第一個處理A 和B,第二個處理第一個半減器的差與借位輸入。
差:第二個半減器的差輸出。
借位:兩個半減器的借位輸出透過一個或閘連接。
使用與非門構造半減器和或門,然後組合它們形成全減器。
5. 建構乘法門
二進位乘法
實現兩個二進制數的乘法。
第一步:使用與閘進行位元乘法。
第二步:使用全加法串聯進行連續的加法。
第三部:實現移位和累加。
6. 構造暫存器
D 觸發器
儲存一位二進位資訊。
第一步:使用與非閘建立鎖存器(Latch)。
第二步:將鎖存器擴展成觸發器(Flip-flop)。
暫存器
儲存多位二進制數。
將多個D 觸發器並行連接,每個儲存一位。
7. 構造時鐘
振盪器
提供週期性的時鐘信號。
使用與非閘創建回饋迴路,產生連續的振盪。
結論
與非閘因其能夠建構任何其他邏輯閘和複雜電路的能力而被稱為“通用邏輯閘”。透過上述方法,可以利用與非閘來建構出複雜的加法、減法、乘法以及儲存和時鐘電路,這是電腦和數字系統中進行算術運算的基礎。在現代集成電路設計中,與非閘因其簡單性和多功能性而廣泛使用。
在B² Network 的實踐中,透過與非閘可以構造任何的計算邏輯。
密碼學中的承諾
承諾在密碼學和區塊鏈中使用非常廣泛,像SHA 256、Merkle Tree、零知識證明中的KZG 都是承諾,像上文中介紹的ZK-Rollup 將零知識證明作為Rollup 的承諾, OP-Rollup將虛擬機器內的字節碼作為Rollup 的承諾。
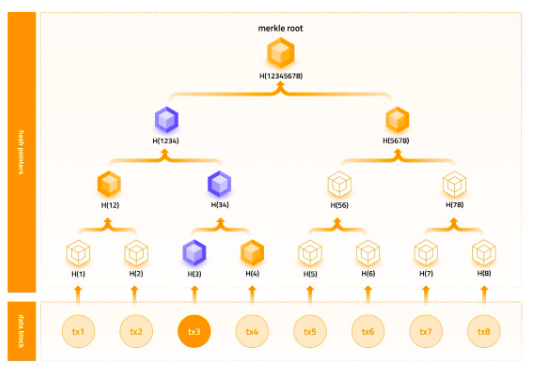
我們透過Merkle Tree 來詳細說明如何使用承諾:
commit:Prover 將所有的value 計算哈希,哈希作為二叉樹的葉子節點,不斷向上進行哈希計算,最終生成Merkle Tree,發布tree root hash 作為承諾。
reveal:Prover 揭露一個葉節點對應的value,以及其branch。
check:Verifier 通過揭露的value、branch 計算哈希,最終與發布的承諾進行對比,進行驗證。
如下圖範例:
commit:Prover 將tx 1、tx 2 ……tx 8 分別計算哈希,得到H( 1)、H( 2)......H( 8),不斷兩兩進行哈希計算,最終生成圖中的二叉樹結構,即Merkle Tree,將Merkle Tree 的root 節點的值H( 12345678)作為承諾進行發布。
reveal:Prover 揭露一個葉子結點對應的value,如tx 3 ,以及其branch(H( 4) -> H( 12) -> H( 5678))。
check:Verifier 通過揭露的tx 3 和branch(H( 4) -> H( 12) -> H( 5678))進行計算並驗證承諾:
計算tx 3 的哈希H( 3)
將H( 3)與branch 中的H( 4)進行哈希,得到H( 34)
將H( 34)與branch 中的H( 12)計算哈希,得到H( 1234)
將H( 1234)與branch 中的H( 5678)計算哈希,得到H( 12345678)
將H( 12345678)與公佈的承諾進行驗證
B² Network 的零知識證明驗證承諾
B² Network 是建構在比特幣網路的ZK-Rollup 二層解決方案。
Bitcoin 上ZK-Rollup 的限制
由於比特幣的圖靈不完備限制,導致比特幣網絡上沒有辦法進行零知識證明的驗證,因此ZK-Rollup 的傳統解決方案,在一層區塊鍊網絡驗證零知識證明的實現方式,是沒辦法在比特幣網路上實現的。
ZK-Rollup 只將零知識證明和Rollup 的數據聚合通過Taproot 寫入比特幣網絡,只能保證ZK-Rollup 的數據錨定在了比特幣網絡,無法被篡改,但是無法保證ZK-Rollup 的交易的有效性、正確性,也沒辦法利用比特幣網路的強大共識能力保證二層ZK-Rollup 的安全性。
因此,一定需要在比特幣網路上進行ZK-Rollup 的確認。
零知識證明與算術電路
零知識證明
在零知識證明中,算術電路是用來建構一個證明,證明者知道某些秘密訊息,而不需要透露這些資訊本身。
零知識證明使用算術電路產生證明:
生成證明
一旦算術電路建立,證明者將使用他們的秘密輸入來計算電路的輸出。在這個過程中,證明者也會產生額外的資訊(如零知識證明特有的承諾和隨機數),這些資訊用於建立證明。
驗證證明
證明者將他們的證明發送給驗證者。驗證者不知道證明者的秘密輸入,但他們有電路的描述和證明者的證明。驗證者透過執行電路的相同計算,並比較其結果與證明者所提供的證明,來驗證證明的有效性。
算術電路
算術電路通常表示為有向無環圖(DAG),其中每個節點代表一個算術操作,邊代表操作之間的資料流。輸入節點代表電路的輸入值,通常是一些數字或變量,而內部節點代表算術操作。電路的輸出是最終的計算結果。
算術電路中的基礎電路閘:
加法門(Addition Gate)
乘法門(Multiplication Gate)
根據上文與非閘的介紹,算術電路是可以透過將加法閘轉換為與非閘,將乘法閘轉換為與非閘,最終算術電路轉換為基於與非閘的邏輯閘電路。
零知識證明驗證承諾
零知識證明的驗證程式本身就是一個算術電路,透過將算術電路轉換為基於與非閘的邏輯閘,實際上可以將零知識證明的驗證程式轉換為基於與非閘的邏輯閘電路。
與非閘透過比特幣腳本實現,將Bit Value Commitment 作為輸入和輸出組裝成邏輯閘,實現邏輯閘約束。
可簡記為
實際上,可以透過比特幣腳本實現與非門,再由與非閘構造出加法門和乘法門,加法門和乘法門組合成算術電路,最終構造出零知識證明的驗證程序。但是由於涉及的門電路非常多,構造出的比特幣腳本也非常龐大,無法在比特幣網路上真正運作。
將Bit Value Commitment 作為輸入和輸出組裝成邏輯閘,每一個帶有不同輸入和輸出的邏輯閘作為葉子節點,組合成電路二叉樹,發布的Circuit Taproot 是二叉樹的root,減小了發布的尺寸。
Circuit Taproot 作為B² Rollup 在一層區塊鍊網絡比特幣上提交的承諾。不同於傳統的ZK-Rollup 可以在一層網絡執行驗證,B² Rollup 無法在比特幣上直接執行驗證。但可以參考Optimistic Rollup 的方式,針對承諾提供挑戰機制,透過挑戰機製完成Circuit Taproot 承諾的確認。
驗證和回應協議
有別於BitVM 需要事先簽署兩方間的鏈下交易。 B² Network 採用發布鎖定獎勵的UTXO 交易,解鎖腳本是一個Taproot 腳本。
具體的解鎖Taproot 腳本是Prover 提前將Circuit Taproot Tree 的每個branch 產生腳本,並給定輸入的哈希。 Challenger 利用preimage 執行腳本,如果執行的output 和Prover 的提交不一致,就能利用MAST(Taproot Merklized Abstract Syntax Tree,默克爾抽象語法樹)解鎖整個Taproot,從而獲得鎖定的獎金。
由於零知識驗證程式的運作成本很小,而且非常快速,因此比特幣網路上的用戶都可以充當Challenge 機制的觀察者,驗證B² Rollup 提交的承諾,一旦發現承諾不一致,可以立即發起挑戰。
挑戰機制類似於Arbitrum Rollup 的“互動式驗證遊戲”,不斷尋找錯誤執行的邏輯閘計算。為了在眾多邏輯閘中找到錯誤的一個,將會使用二分查找的方式,執行閘電路比特幣腳本。最快找到錯誤分支的挑戰者,可以在比特幣網路上解鎖鎖定獎勵的UTXO,從而獲得獎勵。
同時,Taproot 鎖定腳本中的一個分支是時間鎖腳本,當沒有Challenge 成功挑戰,Prover 將在挑戰期結束後,透過時間鎖腳本解鎖UTXO,取回獎勵。
總結
B² Network 通過Ordinals Protocol,將rollup 的data 和proof 聚合後寫入Tapscript 中,利用不同的去中心化儲存協議保存rollup 明細數據,有效地保證了rollup 的data availability。
B² Network 通過將zero-knowledge proof verification commitment 記錄在Bitcoin 上,允許任意的觀察者針對commitment 進行挑戰的機制,可以繼承Bitcoin 的安全性,在Bitcoin 上共識rollup 的數據。



