서론: 시스템 아키텍처에서 재현성 보장까지

기존 블록체인 시스템에서 작업 증명은 보안을 보장하기 위해 해싱 연산의 무작위성에 주로 의존합니다. 그러나 Gonka PoW 2.0은 더욱 복잡한 과제에 직면합니다. 대규모 언어 모델 기반 계산에서 예측 불가능한 결과를 보장하는 동시에 모든 정직한 노드가 동일한 계산 과정을 재현하고 검증할 수 있도록 보장하는 방법입니다. 이 글에서는 MLNode가 신중하게 설계된 시딩 메커니즘과 결정론적 알고리즘을 통해 이러한 목표를 어떻게 달성하는지 자세히 살펴봅니다.

구체적인 기술 구현을 살펴보기 전에 먼저 PoW 2.0 시스템 아키텍처의 전반적인 설계와 재현성이 그 안에서 어떤 중요한 역할을 하는지 이해해야 합니다.

1. PoW 2.0 시스템 아키텍처 개요

1.1 계층형 아키텍처 설계

Gonka PoW 2.0은 블록체인 수준부터 계산 실행 수준까지 재현성을 보장하기 위해 계층화된 아키텍처를 채택합니다.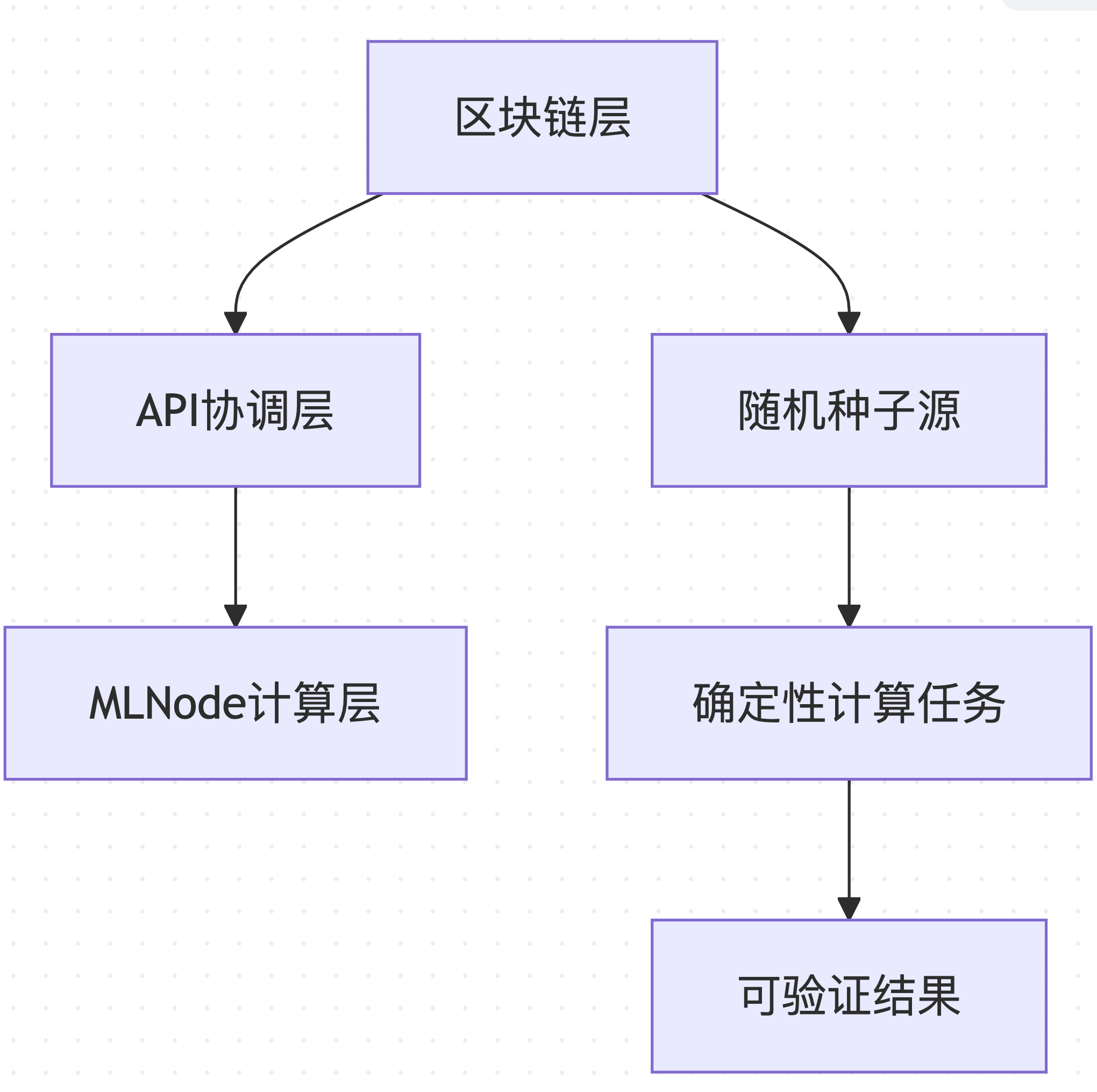

데이터 출처 : decentralized-api/internal/poc 및 mlnode/packages/pow의 아키텍처 설계 기반

이러한 계층적 설계를 통해 전반적인 일관성과 검증 가능성을 유지하면서 시스템의 다양한 구성 요소를 독립적으로 최적화할 수 있습니다.

1.2 재현성의 핵심 목표

PoW 2.0 시스템의 재현성 설계는 다음과 같은 핵심 목표를 달성합니다.

1. 계산 공정성 : 모든 노드가 동일한 계산 과제에 직면하도록 보장

2. 결과 검증 : 모든 정직한 노드는 계산 결과를 재현하고 검증할 수 있습니다.

3. 부정행위 방지 보장 : 계산 전 오류 및 결과 변조를 계산적으로 불가능하게 만듦

4. 네트워크 동기화 : 분산 환경에서 상태 일관성 보장

이러한 목표는 모두 PoW 2.0의 재현 가능한 설계의 기반을 형성하여 시스템의 보안과 공정성을 보장합니다.

2. 시드 시스템: 다단계 무작위성의 통합 관리

시스템 아키텍처를 이해한 후에는 재현성을 확보하기 위한 핵심 기술인 시드 시스템을 자세히 살펴봐야 합니다. 시드 시스템은 다단계 무작위성 관리를 통해 계산의 일관성과 예측 불가능성을 보장합니다.

2.1 종자 유형 및 특정 대상

Gonka PoW 2.0은 각각 특정한 계산 목표를 달성하는 4가지 유형의 시드를 설계합니다.

네트워크 수준 시드

데이터 출처 : decentralized-api/internal/poc/random_seed.go#L90-L111

목표 : 각 에포크에서 전체 네트워크에 통합된 난수 기반을 제공하여 모든 노드가 동일한 글로벌 난수 소스를 사용하도록 보장합니다.

네트워크 수준 시드는 전체 시스템의 무작위성의 기반이 되며, 블록체인 거래를 통해 네트워크의 모든 노드가 동일한 무작위성 기반을 사용하도록 보장합니다.

작업 수준 시드

데이터 출처 : mlnode/packages/pow/src/pow/random.py#L9-L21

목표 : SHA-256 해싱을 여러 라운드 거쳐 엔트로피 공간을 확장하여 모든 계산 작업에 적합한 고품질 난수 생성기를 만드는 것입니다.

작업 수준 시드는 엔트로피 공간을 확장하여 각 특정 컴퓨팅 작업에 대해 고품질의 무작위성을 제공합니다.

노드 수준 시드

데이터 출처 : 시드 문자열 생성 패턴 `f"{hash_str}_{public_key}_nonce{nonce}"`

목표 : 충돌과 중복을 방지하기 위해 서로 다른 노드와 서로 다른 nonce 값이 완전히 다른 계산 경로를 생성하도록 보장합니다.

노드 수준 시드는 노드 공개 키와 nonce 값을 결합하여 각 노드의 계산 경로가 고유하도록 보장합니다.

타겟 벡터 시드

데이터 출처 : mlnode/packages/pow/src/pow/random.py#L165-L177

목표 : 모든 노드가 동일한 고차원 구형 위치를 향해 최적화된 전체 네트워크에 대한 통합된 타겟 벡터를 생성합니다.

타겟 벡터 시드는 네트워크의 모든 노드가 동일한 목표를 향해 계산하도록 보장하는데, 이는 결과의 일관성을 검증하는 데 중요합니다.

2.2 종자 수명 주기 관리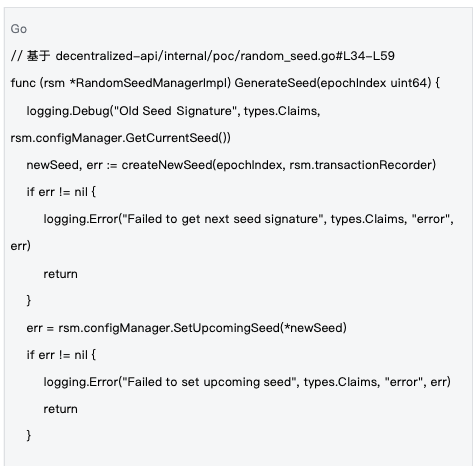

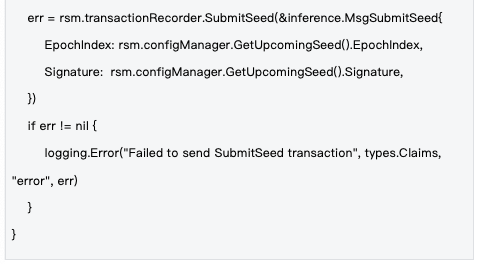
관리 메커니즘 : 시드는 에포크(epoch) 단위로 관리됩니다. 각 에포크가 시작될 때마다 새로운 시드가 생성되고, 블록체인 트랜잭션을 통해 전체 네트워크에 동기화되어 모든 노드가 동일한 난수 기반을 사용하도록 보장합니다.

씨앗의 수명주기 관리를 통해 무작위성의 적시성과 일관성이 보장되며, 시스템의 안전한 운영을 위한 중요한 보장입니다.

3. LLM 구성요소의 시드 기반 생성 메커니즘

이제 시드 시스템을 명확하게 이해했으므로, 이러한 시드를 LLM 구성 요소 생성에 적용하는 방법을 살펴보겠습니다. 이것이 재현성을 확보하는 핵심입니다.

3.1 모델 가중치의 무작위 초기화

모델 가중치를 무작위로 초기화해야 하는 이유는 무엇입니까?

기존 딥러닝에서는 모델 가중치를 사전 학습을 통해 얻었습니다. 그러나 PoW 2.0에서는 다음을 보장하기 위해 다음과 같은 작업이 필요합니다.

1. 계산 작업의 예측 불가능성 : 고정된 가중치로 인해 동일한 입력이 예측 가능한 출력을 생성하지 않습니다.

2. ASIC 저항성 : 특수 하드웨어는 고정된 무게에 최적화될 수 없습니다.

3. 공정한 경쟁 : 모든 노드가 동일한 무작위 초기화 규칙을 사용합니다.

데이터 출처 : mlnode/packages/pow/src/pow/random.py#L71-L88

모델 가중치를 무작위로 초기화하는 것은 계산적 예측 불가능성과 공정성을 보장하는 핵심 단계입니다.

가중치 초기화를 위한 결정론적 프로세스

데이터 소스 : mlnode/packages/pow/src/pow/compute/model_init.py#L120-L125

주요 특징 :

• 모든 노드가 동일한 가중치를 생성하도록 하기 위해 블록 해시를 난수 시드로 사용합니다.

• 가중치 초기화를 위해 정규 분포 N(0, 0.02²)를 사용합니다.

• 메모리 최적화를 위해 다양한 데이터 유형(예: float16)을 지원합니다.

이러한 결정론적 프로세스는 서로 다른 노드가 동일한 조건에서 정확히 동일한 모델 가중치를 생성하도록 보장합니다.

3.2 입력 벡터 생성 메커니즘

왜 무작위 입력 벡터가 필요한가요?

기존 PoW는 고정된 데이터(예: 거래 목록)를 입력으로 사용하지만 PoW 2.0은 다음을 보장하기 위해 각 nonce에 대해 다른 입력 벡터를 생성해야 합니다.

1. 검색 공간의 연속성 : 다른 nonce는 다른 계산 경로에 해당합니다.

2. 예측할 수 없는 결과 : 입력의 작은 변화가 출력의 큰 차이로 이어짐

3. 검증의 효율성 : 검증자는 동일한 입력을 빠르게 재현할 수 있습니다.

데이터 출처 : mlnode/packages/pow/src/pow/random.py#L129-L155

무작위 입력 벡터를 생성하면 계산의 다양성과 예측 불가능성이 보장됩니다.

입력 생성을 위한 수학적 기초

데이터 출처 : mlnode/packages/pow/src/pow/random.py#L28-L40

기술적 특징 :

• 각 nonce는 고유한 시드 문자열에 해당합니다.

• 표준 정규 분포를 사용하여 임베딩 벡터 생성

• 효율성 향상을 위한 배치 생성 지원

이러한 수학적 기초는 입력 벡터의 품질과 일관성을 보장합니다.

3.3 출력 순열 생성

왜 순열을 출력해야 할까요?

LLM의 출력 계층에서는 어휘가 일반적으로 큽니다(예: 32,000~100,000 토큰). 계산 복잡도를 높이고 특정 최적화를 방지하기 위해 시스템은 출력 벡터를 무작위로 순열합니다.

데이터 출처 : mlnode/packages/pow/src/pow/random.py#L158-L167

출력 순열은 계산의 복잡성을 증가시키고 시스템의 보안을 향상시킵니다.

배열의 적용 메커니즘

데이터 출처 : mlnode/packages/pow/src/pow/compute/compute.py의 처리 로직 기반

디자인 목표 :

• 계산 과제의 복잡성 증가

• 특정 어휘 위치 최적화 방지

• 검증을 지원하기 위한 결정론 유지

이러한 적용 메커니즘은 배열의 유효성과 일관성을 보장합니다.

4. 타겟 벡터와 구 사이의 거리 계산

LLM 구성 요소의 생성 메커니즘을 이해한 후, PoW 2.0의 핵심적인 계산 과제인 타겟 벡터와 구 사이의 거리를 계산하는 문제를 더 자세히 살펴보겠습니다.

4.1 타겟 벡터란 무엇인가요?

목표 벡터는 PoW 2.0 계산 과제의 "정점"입니다. 모든 노드는 모델 출력을 미리 정해진 고차원 벡터에 최대한 가깝게 만들려고 노력합니다.

타겟 벡터의 수학적 속성

데이터 출처 : mlnode/packages/pow/src/pow/random.py#L43-L56

주요 특징 :

• 벡터는 고차원 단위 구(||target|| = 1)에 있습니다.

• 마르살리아의 방법을 사용하여 구 전체에 균일한 분포를 보장합니다.

• 모든 차원은 선택될 확률이 동일합니다.

목표 벡터의 수학적 속성은 계산 과제에서 공정성과 일관성을 보장합니다.

4.2 구면의 결과를 비교하는 이유는 무엇입니까?

수학적 이점

1. 정규화의 장점 : 구면의 모든 벡터는 단위 길이를 가지므로 벡터 크기의 영향을 제거함

2. 기하학적 직관 : 구면의 유클리드 거리는 각거리와 직접 대응합니다.

3. 수치적 안정성 : 큰 수치 범위로 인한 계산 불안정성을 방지합니다.

고차원 기하학의 특수한 속성

고차원 공간(예: 4096차원 어휘 공간)에서 구형 분포는 반직관적인 속성을 갖습니다.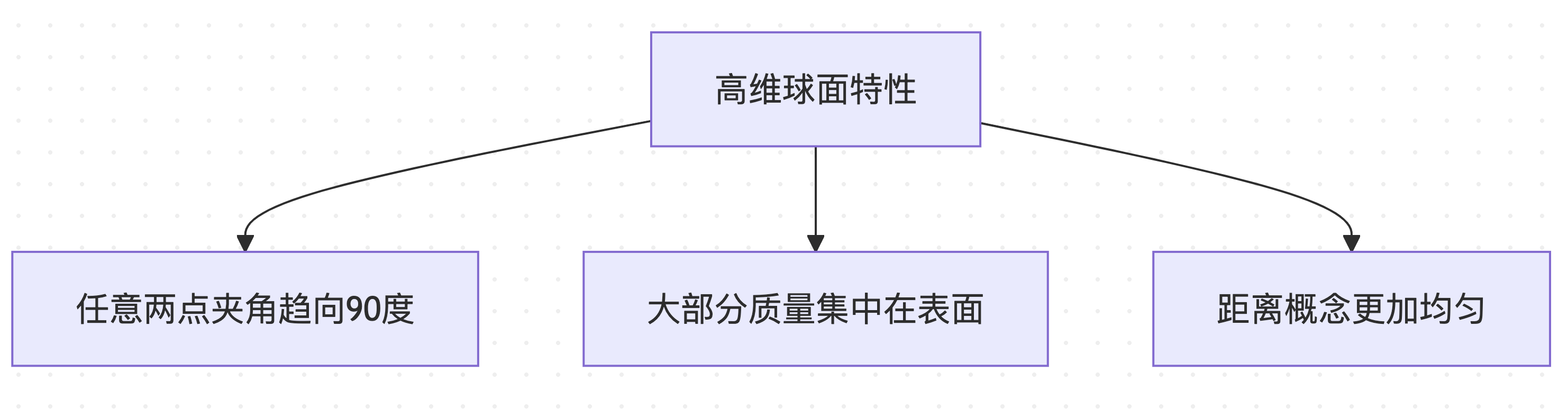

이러한 특수한 속성으로 인해 구면 거리 계산은 이상적이고 계산적으로 어려운 측정 기준이 됩니다.

4.3 r_target 추정 및 PoC 단계 초기화

r_target의 개념과 계산

r_target은 "성공적인" 계산 결과에 대한 거리 임계값을 정의하는 핵심 난이도 매개변수입니다. r_target보다 작은 거리를 갖는 결과는 유효한 작업 증명으로 간주됩니다.

데이터 출처 : decentralized-api/mlnodeclient/poc.go#L12-L14

Gonka PoW 2.0에서 r_target의 기본값은 1.4013564660458173으로 설정됩니다. 이 값은 계산 난이도와 네트워크 효율성의 균형을 맞추기 위해 광범위한 실험과 통계 분석을 통해 결정되었습니다. 시스템에는 동적 조정 메커니즘이 있지만, 대부분의 경우 이 기본값과 유사합니다.

PoC 단계에서 r_target 초기화

각 PoC(계산 증명) 단계가 시작될 때 시스템은 다음을 수행해야 합니다.

1. 네트워크 컴퓨팅 파워 평가 : 과거 데이터를 기반으로 현재 네트워크의 총 컴퓨팅 파워를 추정합니다.

2. 난이도 매개변수 조정 : 안정적인 블록 시간을 유지하기 위해 적절한 `r_target` 값을 설정합니다.

3. 네트워크 전체 매개변수 동기화 : 모든 노드가 동일한 `r_target` 값을 사용하는지 확인합니다.

기술 구현 :

• r_target 값은 블록체인 상태를 통해 모든 노드에 동기화됩니다.

• 각 PoC 단계는 다른 r_target 값을 사용할 수 있습니다.

• 적응형 조정 알고리즘은 이전 단계의 성공률을 기반으로 난이도를 조정합니다.

이러한 초기화 메커니즘은 네트워크의 안정적인 운영과 공정성을 보장합니다.

5. 재현성에 대한 엔지니어링 보증

핵심 알고리즘을 이해한 후에는 엔지니어링 구현에서 재현성을 확보하는 방법에 집중해야 합니다. 이는 실제 구축 환경에서 시스템의 안정적인 작동을 보장하는 핵심 요소입니다.

5.1 결정론적 컴퓨팅 환경

데이터 출처 : mlnode/packages/pow/src/pow/compute/model_init.py의 환경 설정 기반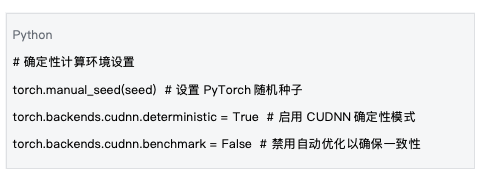

결정론적 컴퓨팅 환경을 구축하는 것은 재현성을 보장하는 기초입니다.

5.2 수치 정밀도 관리

수치적 정밀도 관리를 통해 다양한 하드웨어 플랫폼에서 계산 결과의 일관성을 보장합니다.

5.3 크로스 플랫폼 호환성

시스템 설계는 다양한 하드웨어 플랫폼의 호환성을 고려합니다.

- CPU 대 GPU : CPU와 GPU 모두에서 동일한 계산 결과를 생성하는 것을 지원합니다.

- 다양한 GPU 모델 : 표준화된 수치 정밀도를 통해 일관성을 보장합니다.

- 운영 체제 차이점 : 표준 수학 라이브러리 및 알고리즘 사용

다양한 플랫폼 간 호환성을 통해 다양한 배포 환경에서 시스템의 안정적인 작동이 보장됩니다.

6. 시스템 성능 및 확장성

재현성을 보장하는 것 외에도 시스템은 우수한 성능과 확장성을 갖춰야 하며, 이는 네트워크의 효율적인 운영을 보장하는 데 핵심입니다.

6.1 병렬화 전략

데이터 소스 : mlnode/packages/pow/src/pow/compute/model_init.py#L26-L53

병렬화 전략은 현대 하드웨어의 계산 능력을 최대한 활용합니다.

6.2 메모리 최적화

시스템은 다양한 전략을 통해 메모리 사용을 최적화합니다.

- 배치 최적화 : GPU 활용도를 극대화하기 위해 배치 크기를 자동으로 조정합니다.

-정밀도 선택 : float16을 사용하여 메모리 사용량을 줄입니다.

- 그래디언트 관리 : 추론 모드에서 그래디언트 계산 비활성화

메모리 최적화는 리소스가 제한된 환경에서 효율적인 시스템 운영을 보장합니다.

요약: 재현 가능한 설계의 엔지니어링 가치

PoW 2.0의 재현 가능한 설계에 대한 심층 분석을 거쳐, 기술적 성과와 엔지니어링 가치를 요약할 수 있습니다.

핵심기술 성과

1. 다단계 시드 관리 : 컴퓨팅에서 결정성과 예측 불가능성 간의 균형을 보장하기 위해 네트워크 수준에서 작업 수준까지 완전한 시드 시스템

2. LLM 구성 요소의 체계적 무작위화 : 모델 가중치, 입력 벡터 및 출력 순열을 위한 통합 무작위화 프레임워크

3. 고차원 기하학의 엔지니어링 응용 : 구면 기하학적 속성을 사용하여 공정한 컴퓨팅 과제 설계

4. 크로스 플랫폼 재현성 : 표준화된 알고리즘과 정밀 제어를 통해 다양한 하드웨어 플랫폼 간 일관성을 보장합니다.

이러한 기술적 성과는 모두 PoW 2.0의 재현 가능한 디자인의 핵심을 형성합니다.

시스템 설계의 혁신적 가치

블록체인 보안을 유지하는 동시에, Gonka PoW 2.0은 무의미한 해싱 작업에서 가치 있는 AI 연산으로 컴퓨팅 리소스를 성공적으로 전환합니다. 재현 가능한 설계는 시스템 공정성과 보안을 보장할 뿐만 아니라 미래의 "의미 있는 채굴" 모델을 위한 실행 가능한 기술 패러다임을 제공합니다.

기술적 영향 :

• 분산 AI 컴퓨팅을 위한 검증 가능한 실행 프레임워크 제공

• 복잡한 AI 작업과 블록체인 합의의 호환성 입증

• 새로운 유형의 작업 증명을 위한 설계 표준 수립

신중하게 설계된 시드 시스템과 결정론적 알고리즘을 통해 Gonka PoW 2.0은 기존의 "폐기물 기반 보안"에서 "가치 기반 보안"으로 근본적인 전환을 이루어 블록체인 기술의 지속 가능한 발전을 위한 새로운 길을 열었습니다.

참고: 이 문서는 Gonka 프로젝트의 실제 코드 구현을 기반으로 합니다. 모든 코드 예제와 기술 설명은 해당 프로젝트의 공식 코드 저장소에서 가져왔습니다.

Gonka.ai 소개

Gonka는 효율적인 AI 컴퓨팅 파워를 제공하도록 설계된 탈중앙화 네트워크입니다. Gonka의 설계 목표는 글로벌 GPU 컴퓨팅 파워를 최대한 활용하여 의미 있는 AI 워크로드를 완료하는 것입니다. 중앙화된 게이트키퍼를 제거함으로써 Gonka는 개발자와 연구자에게 컴퓨팅 리소스에 대한 허가 없는 접근을 제공하는 동시에 모든 참여자에게 GNK 토큰을 보상으로 제공합니다.

Gonka는 미국 AI 개발사 Product Science Inc.에서 인큐베이팅되었습니다. 웹 2 업계 베테랑이자 Snap Inc.의 전 핵심 제품 책임자였던 Libermans 형제가 설립한 이 회사는 2023년 OpenAI 투자자 Coatue Management, Solana 투자자 Slow Ventures, K5, Insight, Benchmark Partners 등의 투자자들로부터 1,800만 달러를 성공적으로 유치했습니다. 이 프로젝트의 초기 참여자로는 6 Blocks, Hard Yaka, Gcore, Bitfury 등 웹 2-웹 3 분야의 유명 기업들이 있습니다.

공식 웹사이트 | Github | X | Discord | 백서 | 경제 모델 | 사용자 매뉴얼