대화식 증명을 비대화식 증명으로 변환하는 방법은 무엇입니까?
머리말
머리말
암호화의 영지식 증명 기술은 사설 컴퓨팅, zkRollup 등을 포함하여 web3 세계에서 광범위한 응용 프로그램을 보유하고 있습니다. 그 중 Layer 2 프로젝트 FOX에서 사용하는 FOAKS는 영지식 증명 알고리즘입니다. 위에서 언급한 일련의 응용 프로그램 중에서 두 가지 속성이 영지식 증명 알고리즘에 매우 중요합니다. 즉, 알고리즘의 효율성과 상호 작용성입니다.
알고리즘 효율성의 중요성은 자명합니다.효율적인 알고리즘은 시스템 런타임을 크게 줄여 클라이언트 대기 시간을 줄이고 사용자 경험과 효율성을 크게 향상시킵니다.또한 이것이 FOAKS가 선형 증명 시간을 달성하기 위해 노력하는 중요한 이유입니다.
반면에 암호화의 관점에서 볼 때 영지식 증명 시스템의 설계는 증명자와 검증자 간의 여러 라운드의 상호 작용에 의존하는 경우가 많습니다. 예를 들어, 영지식 증명을 소개하는 많은 대중 과학 기사에서 사용되는 "영지식 동굴" 이야기에서 증명의 실현은 알리바바(증명자)와 기자 간의 여러 차례의 정보 전송 및 상호 작용에 달려 있습니다. 확인자). 그러나 실제로 많은 애플리케이션 시나리오에서 상호 작용에 의존하면 시스템을 더 이상 사용할 수 없게 되거나 지연이 크게 증가합니다. zkRollup 시스템과 마찬가지로 검증자(즉, FOX의 폴더)가 검증자와의 상호 작용에 의존하지 않고 로컬에서 올바른 증명 값을 계산할 수 있을 것으로 기대합니다.
첫 번째 레벨 제목
영지식증명의 도전
영지식 증명 알고리즘은 응용 프로그램의 보급으로 큰 인기를 얻었으며 최근에는 FOAKS, Orion, zk-stark 등 다양한 알고리즘도 탄생했습니다. 암호화 분야의 초기 시그마 프로토콜뿐만 아니라 이러한 알고리즘의 핵심 증명 논리는 증명자(Prover)가 먼저 특정 값을 검증자(Verifier)에게 보내고 검증자는 다음을 통해 챌린지(Challenge)를 생성한다는 것입니다. 임의로 생성된 챌린지 값은 증명자에게 전송되며, 증명자는 검증자를 통과할 확률이 높은 응답을 하기 위해 실제 지식이 필요합니다. 예를 들어 영지식동굴에서 기자가 동전을 던지고 알리바바에게 좌우에서 나오라고 했는데 여기서 '좌우'는 알리바바에게 도전이다. 실패 확률의 절반이 됩니다.
여기서 우리는 챌린지 생성이 중요한 단계라는 것을 알 수 있습니다. 두 가지 요구 사항이 있습니다. 즉, 무작위 및 증명자가 예측할 수 없습니다. 첫째, 임의성은 확률적 속성을 보장합니다. 두 번째 포인트는 증명자가 챌린지 값을 예측할 수 있다면 프로토콜의 보안이 깨졌다는 것입니다. 증명자는 지식 없이 검증을 통과할 수 있습니다. 비유를 계속할 수 있습니다. 에서 나오는, 그는 철자가 없더라도 미리 그쪽에 들어갈 수 있으며 결과는 당신이 동의를 통과 할 수 있음을 보여줍니다.
첫 번째 레벨 제목
해시 함수
해시 함수의 이름은 우리에게 낯설지 않을 수 있는데, 비트코인 합의 프로토콜 POW에서 채굴하는 수학적인 문제든, 데이터의 양을 압축하거나, 메시지 검증 코드를 구성하는 등, 해시 함수가 있습니다. . 위에서 언급한 여러 가지 프로토콜 중에서 해시 함수의 다양한 속성이 실제로 사용됩니다.
특히 보안 해시 함수의 속성에는 다음이 포함됩니다.
압축성: 결정론적 해시 함수는 모든 길이의 메시지를 고정된 길이로 압축할 수 있습니다.
효율성: 입력 x가 주어지면 출력 h(x)를 계산하기 쉽습니다.
충돌 방지: 입력 x 1 이 주어지면 다른 입력 x 2 , x 1 x 2 , h(x 1 ) = h(x 2 )를 찾기가 어렵습니다.
해시 함수가 충돌 저항을 만족하는 경우 단방향 속성을 충족해야 합니다. 즉, 출력 y가 주어지면 h(x) = y를 만족하는 x를 찾기가 어렵습니다. 암호학에서는 이론적으로 일방향성을 절대적으로 만족하는 함수를 구성하는 것은 불가능하지만, 해쉬함수는 기본적으로 실전에서 일방향함수라고 볼 수 있다.
첫 번째 레벨 제목
Fiat-Shamir 휴리스틱(휴리스틱)
실제로 Fiat-Shamir 휴리스틱(Heuristic)은 해시 함수를 이용해 이전에 생성된 스크립트를 해시하여 값을 얻고, 이를 챌린지 값으로 사용하는 것입니다.
이미지 설명
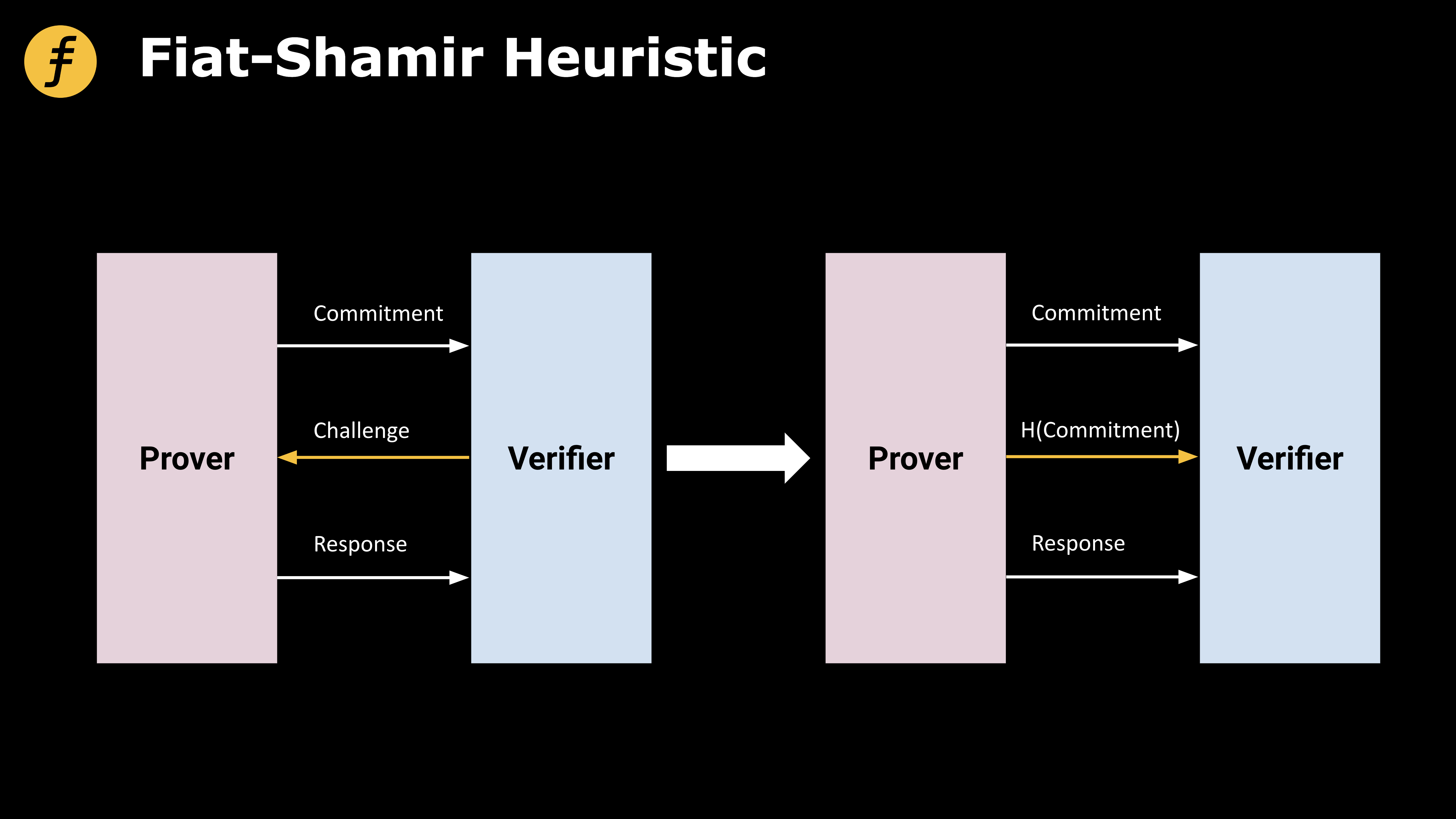
첫 번째 레벨 제목
비대화형 FOAKS
이 섹션에서는 FOAKS 프로토콜에서 Fiat-Shamir 휴리스틱의 적용을 구체적으로 보여줍니다. 이는 주로 브레이크다운 부분에서 챌린지를 생성하는 데 사용되어 비대화형 FOAKS를 실현합니다.
이미지 설명

그림 2: 비대화형 증명 FOAKS의 브레이크다운 확인
이제 우리는 해시 함수를 사용하고 증명자가 이 랜덤 벡터를 직접 생성하도록 합니다.
γ0=H(C1, R, r0, r1)라고 하면, 검증기의 검증 계산에서 γ0를 계산하는 이 단계도 추가되어야 합니다. 이 구조에 따르면 Commit이 생성되기 전에 Prover는 Challenge 값을 미리 예측할 수 없으므로 미리 Challenge 값에 따라 "Cheat", 즉 그에 따라 잘못된 Commitment 값을 생성할 수 없음을 알 수 있습니다. .동시에 함수 출력의 해시 임의성에 따라 챌린지 값도 임의성을 만족합니다.
두 번째 점에 대해 Δ =H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 )라고 합니다.
발문
function PC. Commit(ϕ):
Parse was a k × k matrix. The prover locally computes the tensor code encoding C1 ,C2 ,C1 is a k × n matrix,C2 is a n × n matrix.
for i ∈ [n] do
Compute the Merkle tree root Roott=Merkle.Commit(C2 [:, i])
Compute a Merkle tree root R=Merkle.Commit([Root0 ,......Rootn-1 ]), and output R as the commitment.
function PC. Prover(ϕ, X, R)
The prover generates a random vector γ0 ∈ Fk by computing: γ0 =H(C1 , R, r0 , r1 )
Proximity:
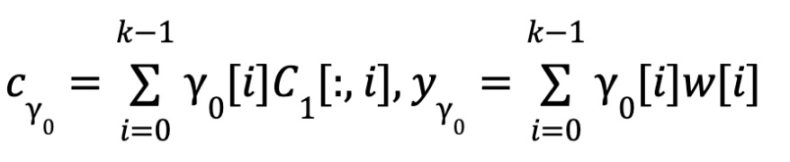
Consistency:
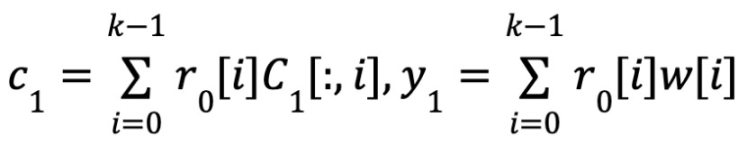
Prover sends c1 , y1 , cγ 0 , yγ 0 to the verifier.
Prover computes a vector Î as challenge, in which Î = H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 )
for idx ∈ Î do
Prover sends C1 [:, idx] and the Merkle tree proof of Rootidx for C2 [:, idx] under R to verifier
function PC. VERIFY_EVAL(ΠX, X, y= ϕ (X), R)
Proximity: ∀idx ∈ Î, Cγ 0 [idx] == <γ0 , C1 [:, idx]> and Ec(yγ 0 ) == Cγ 0
Consistency: ∀idx ∈ Î, C1 [idx] == <γ0 , C1 [:, idx]> and Ec(y1 ) == C1
y==
∀idx ∈ Î, Ec ( C1 [:, idx]) is consistent with ROOTidx, and ROOTidx’s Merkle tree proof is valid.
Output accept if all conditions above holds. Otherwise output reject.
발문
참조
참조
1.Fiat, Amos; Shamir, Adi ( 1987). "How To Prove Yourself: Practical Solutions to Identification and Signature Problems". Advances in Cryptology — CRYPTO' 86. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 263: 186 – 194. doi: 10.1007/3-540-47721-7 _ 12. ISBN 978-3-540-18047-0.
2.https://www.cnblogs.com/zhuowangy 2 k/p/12246575.html



