Vitalik Buterin: 스텔스 주소에 대한 불완전한 가이드

DeFi之道

特邀专栏作者

2023-01-24 02:00

이 기사는 약 5487자로, 전체를 읽는 데 약 8분이 소요됩니다

장기적으로 스텔스 주소 생태계는 영지식 증명에 크게 의존하는 것으로 보입니다.

AI 요약

펼치기

장기적으로 스텔스 주소 생태계는 영지식 증명에 크게 의존하는 것으로 보입니다.

원작자: 비탈릭 부테린

원문 편집: The Way of DeFi

원작자: 비탈릭 부테린

원문 편집: The Way of DeFi

이더리움 생태계에 남아 있는 가장 큰 과제 중 하나는 프라이버시입니다. 퍼블릭 블록체인에 들어가는 모든 것은 기본적으로 퍼블릭입니다. 점점 더 이것은 돈과 금융 거래뿐만 아니라 ENS 이름, POAP, NFT, 소울바운드 토큰 등을 의미합니다. 실제로 Ethereum 응용 프로그램의 전체 제품군을 사용하려면 누구나 보고 분석할 수 있도록 삶의 중요한 부분을 노출해야 합니다.

이러한 상황을 개선하는 방법은 중요한 문제가 되었으며 널리 인식되고 있습니다. 그러나 지금까지 개인 정보 보호 개선에 대한 논의는 ETH 및 주류 ERC 20 토큰의 개인 정보 보호 전송(종종 자체 전송)이라는 특정 사용 사례를 중심으로 이루어졌습니다. 이 게시물은 많은 다른 맥락에서 이더리움의 프라이버시 상태를 개선할 수 있는 다른 종류의 도구인 스텔스 주소의 메커니즘과 사용 사례를 설명합니다.

첫 번째 레벨 제목

스텔스 주소 시스템이란 무엇입니까?

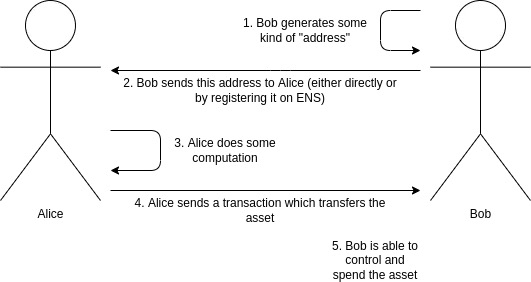
Alice가 Bob에게 자산을 제공하려고 한다고 가정합니다. 이는 일정량의 암호화폐(예: 1 ETH, 500 RAI)이거나 NFT일 수 있습니다. Bob은 자산을 받았을 때 자신이 자산을 얻었다는 사실을 세상이 알기를 원하지 않습니다. 특히 온체인에 하나의 사본만 있는 NFT인 경우 전송이 발생했다는 사실을 숨기는 것은 불가능하지만 수신자가 누구인지 숨기는 것이 더 가능할 수 있습니다. Alice와 Bob도 게으릅니다. 그들은 결제 프로세스가 오늘날과 정확히 동일한 시스템을 원합니다. Bob은 누군가가 그에게 지불할 수 있는 방법을 인코딩하는 일종의 "주소"를 Alice에게 보냅니다(또는 ENS에 등록). 이 정보만으로도 Alice(또는 다른 사람)가 그에게 자산을 보낼 수 있습니다.

이것은 Tornado Cash와 같은 도구에서 제공하는 개인 정보 보호와는 다릅니다. Tornado Cash는 ETH 또는 주요 ERC 20 토큰과 같은 주류 대체 자산의 전송을 숨길 수 있지만(개인적으로 전송하는 데 사용하는 것이 가장 쉽지만) 알려지지 않은 ERC 20 전송에 개인 정보를 추가하는 데 매우 약하고 방법이 없습니다. NFT 전송에 개인 정보를 추가합니다.

암호화폐 결제를 위한 일반적인 워크플로. 개인 정보 보호를 강화하고 싶지만(아무도 자산을 받은 사람이 Bob인지 알 수 없음) 작업 흐름은 동일하게 유지합니다.

스텔스 주소는 이러한 솔루션을 제공합니다. 스텔스 주소는 Alice나 Bob이 생성할 수 있지만 Bob만 제어할 수 있는 주소입니다. Bob은 지출 키 비밀을 생성 및 유지하고 해당 키를 사용하여 스텔스 메타 주소를 생성합니다. 그는 이 메타 주소를 Alice에게 전달합니다(또는 ENS에 등록). Alice는 이 메타 주소에 대한 계산을 수행하여 Bob에게 속한 스텔스 주소를 생성할 수 있습니다. 그런 다음 그녀는 원하는 자산을 이 주소로 보낼 수 있으며 Bob은 해당 자산을 완전히 제어할 수 있습니다. 전송과 함께 그녀는 Bob이 이 주소가 자신의 것임을 발견하는 데 도움이 되는 추가 암호화 데이터(임시 공개 키)를 온체인에 게시합니다.

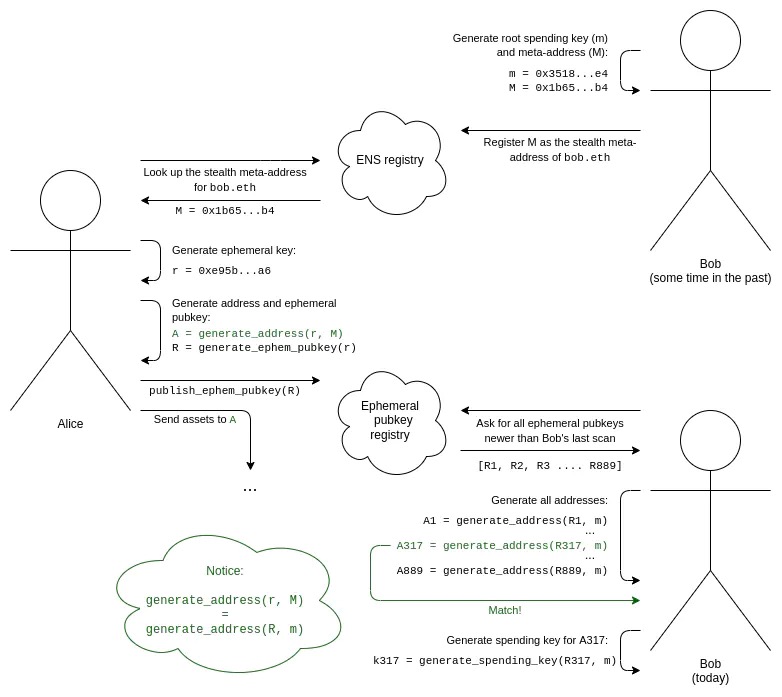
또 다른 방법: 스텔스 주소는 Bob과 동일한 개인 정보 보호 속성을 제공하여 각 트랜잭션에 대해 새 주소를 생성하지만 Bob의 상호 작용이 필요하지 않습니다.

스텔스 주소 체계의 전체 워크플로는 다음과 같습니다.

1. Bob은 루트 지출 키(m)와 스텔스 메타 주소(M)를 생성합니다.

2. Bob은 bob.eth의 스텔스 메타 주소로 M을 등록하기 위해 ENS 레코드를 추가합니다.

3. Alice는 Bob이 bob.eth라는 것을 알고 있다고 가정합니다. Alice는 ENS에서 자신의 스텔스 메타 주소 M을 찾습니다.

4. Alice는 자신만 아는 임시 키를 생성하고 한 번만 사용합니다(이 특정 스텔스 주소 생성).

5. Alice는 자신의 임시 키와 Bob의 메타 주소를 결합하여 스텔스 주소를 생성하는 알고리즘을 사용합니다. 그녀는 이제 이 주소로 자산을 보낼 수 있습니다.

6. Alice는 또한 임시 공개 키를 생성하여 임시 공개 키 레지스트리에 게시합니다(이는 자산을 스텔스 주소로 보낸 첫 번째 트랜잭션과 동일한 트랜잭션에서 수행할 수 있음).

7. Bob이 자신에게 속한 스텔스 주소를 발견하기 위해 Bob은 임시 공개 키 레지스트리를 스캔하여 마지막 스캔 이후 어떤 이유로든 누구에 의해 발행된 임시 공개 키의 전체 목록을 찾아야 합니다.

그것은 모두 암호 스푸핑의 두 가지 용도에 의존합니다. 먼저 공유 비밀을 생성하기 위한 한 쌍의 알고리즘이 필요합니다. 하나는 Alice의 비밀 항목(그녀의 임시 키)과 Bob의 공개 항목(그의 메타 주소)을 사용하는 알고리즘이고 다른 하나는 Bob의 비밀 항목(그의 루트 지출 키)을 사용하는 알고리즘입니다. ) 및 Alice의 공개 트랜잭션(임시 공개 키). 이는 여러 가지 방법으로 수행할 수 있으며, 현대 암호학 분야를 설립한 열매 중 하나인 Diffie-Hellman 키 교환이 바로 그 작업을 수행합니다.

그러나 공유 비밀만으로는 충분하지 않습니다. 공유 비밀에서 개인 키를 생성하면 Alice와 Bob 모두 이 주소에서 사용할 수 있습니다. 우리는 거기서 멈추고 Bob이 자금을 새 주소로 이체하도록 할 수 있지만 그것은 비효율적이고 불필요하게 보안을 감소시킬 것입니다. 그래서 우리는 키 블라인드 메커니즘도 추가했습니다. 한 쌍의 알고리즘, Bob은 공유 비밀을 그의 루트 지출 키와 결합할 수 있고 Alice는 공유 비밀을 Bob의 메타 주소와 결합하여 Alice가 스텔스 주소를 생성할 수 있고 Bob은 스텔스 주소와 Bob의 메타 주소 사이(또는 하나의 스텔스 주소와 다른 주소 사이)에 공개 링크를 생성하지 않고 해당 스텔스 주소에 키를 사용합니다.

첫 번째 레벨 제목

타원 곡선 암호화를 사용한 스텔스 주소

타원 곡선 암호화를 사용하는 스텔스 주소는 2014년 Peter Todd가 Bitcoin과 관련하여 처음 소개했습니다. 이 기술은 다음과 같이 작동합니다(기본 타원 곡선 암호화에 대한 사전 지식이 있다고 가정합니다. 일부 자습서는 여기, 여기 및 여기 참조).

• Bob은 비밀 키 m을 생성하고 M = G * m을 계산합니다. 여기서 G는 타원 곡선의 상호 동의 생성 지점입니다. 보이지 않는 메타 주소는 M의 인코딩입니다.

• Alice는 임시 키 r을 생성하고 임시 공개 키 R = G * r을 게시합니다.

• Alice는 공유 비밀 S = M * r을 계산할 수 있고 Bob은 동일한 공유 비밀 S = m * R을 계산할 수 있습니다.

• 이 주소에 대한 개인 키를 계산하기 위해 Bob(및 Bob 혼자)은 위의 모든 요구 사항을 충족하고 매우 간단한 p = m + hash(S)를 계산할 수 있습니다!

오늘날 이 접근 방식을 지원하고 사용자가 다른 접근 방식을 개발할 수 있는 여지를 남겨두는 이더리움에 대한 스텔스 주소 표준을 정의하려고 시도하는 EIP도 있습니다. 내성 보안). 이제 다음과 같이 생각할 수 있습니다. 스텔스 주소는 어렵지 않고 이론은 견고하며 채택은 단지 구현 세부 사항일 뿐입니다. 그러나 문제는 진정으로 효율적인 구현을 위해서는 꽤 큰 구현 세부 사항을 거쳐야 한다는 것입니다.

첫 번째 레벨 제목

스텔스 주소 및 거래 수수료 지불

누군가 당신에게 NFT를 보낸다고 가정해 봅시다. 귀하의 개인 정보를 염두에 두고 귀하가 제어하는 스텔스 주소로 보냅니다. 지갑은 체인에서 ephem 공개 키를 스캔한 후 이 주소를 자동으로 발견합니다. 이제 이 NFT의 소유권을 자유롭게 증명하거나 다른 사람에게 양도할 수 있습니다. 하지만 문제가 있습니다! 계정에 0 ETH가 있으므로 거래 수수료를 지불할 수 없습니다. ERC-4337 토큰 지불자도 대체 가능한 ERC 20 토큰으로만 작동하기 때문에 작동하지 않습니다. 공개적으로 볼 수 있는 링크를 생성하기 때문에 기본 지갑에서 ETH를 보낼 수 없습니다.

이 문제를 해결하는 "쉬운" 방법이 있습니다. ZK-SNARK를 사용하여 자금을 이체하고 수수료를 지불하기만 하면 됩니다! 그러나 이것은 많은 가스를 소비하고 단일 전송에는 수십만 가스가 필요합니다.

또 다른 영리한 접근 방식은 전문화된 거래 집계자(MEV 용어의 "추적자")를 신뢰하는 것입니다. 이러한 애그리게이터를 통해 사용자는 온체인 거래에 대해 지불하는 데 사용할 수 있는 "티켓" 세트를 구매하기 위해 한 번 지불할 수 있습니다. 사용자가 다른 것을 포함하지 않는 스텔스 주소에서 NFT를 사용해야 하는 경우 Chaumian 블라인드 체계를 사용하여 인코딩된 티켓 중 하나를 애그리게이터에 제공합니다. 이것은 1980년대와 1990년대에 제안된 중앙 집중식 개인 정보 보호 전자 현금 제안에 사용된 원래 프로토콜입니다. 찾는 사람은 "티켓"을 수락하고 트랜잭션이 블록에서 성공적으로 수락될 때까지 무료로 번들에 트랜잭션을 반복적으로 포함합니다. 관련된 자금의 양이 적고 거래 수수료를 지불하는 데만 사용할 수 있기 때문에 신뢰 및 규제 문제는 이러한 중앙 집중식 개인 정보 보호 전자 현금의 "완전한" 구현보다 훨씬 낮습니다.

첫 번째 레벨 제목

스텔스 주소와 별도의 지출 및 보기 키

모든 작업을 수행하는 하나의 마스터 "루트 지출 키" 대신 Bob이 별도의 루트 지출 키와 보기 키를 원한다고 가정합니다. 키를 보면 Bob의 모든 스텔스 주소를 볼 수 있지만 지출할 수는 없습니다.

타원 곡선 세계에서 이것은 매우 간단한 암호화 트릭을 사용하여 해결할 수 있습니다.

• Bob의 메타 주소 M은 이제 (K, V) 형식이며 G * k 및 G * v로 인코딩됩니다. 여기서 k는 지출 키이고 v는 보기 키입니다.

• 이제 공유 비밀은 S = V * r = v * R입니다. 여기서 r은 여전히 Alice의 임시 키이고 R은 여전히 Alice의 임시 공개 키입니다.

• 스텔스 주소의 공개 키는 P = K + G * hash(S)이고 개인 키는 p = k + hash(S)입니다.

첫 번째 영리한 암호화 단계(공유 비밀 생성)는 보기 키를 사용하고 두 번째 영리한 암호화 단계(스텔스 주소와 개인 키를 생성하는 Alice와 Bob의 병렬 알고리즘)는 루트 지출 키를 사용합니다.

여기에는 많은 사용 사례가 있습니다. 예를 들어 Bob이 POAP를 수신하려는 경우 Bob은 자신의 POAP 지갑(또는 덜 안전한 웹 인터페이스)에 보기 키를 제공하여 체인을 스캔하고 인터페이스에 POAP 권한을 사용하지 않고도 모든 POAP를 볼 수 있습니다.

전체 임시 공개 키 세트를 보다 쉽게 스캔하기 위한 한 가지 기술은 각 임시 공개 키에 보기 태그를 추가하는 것입니다. 위의 메커니즘에서 이를 수행하는 한 가지 방법은 보기 레이블을 공유 비밀의 바이트(예: S 모듈로 256의 x 좌표 또는 hash(S)의 첫 번째 바이트)로 만드는 것입니다.

이런 식으로 Bob은 공유 비밀을 계산하기 위해 각 임시 공개 키에 대해 하나의 타원 곡선 곱셈을 수행하면 되고 전체 주소를 생성하고 확인하기 위해 Bob이 더 복잡한 계산을 수행하는 데 필요한 시간은 1/256뿐입니다.

첫 번째 레벨 제목

스텔스 주소 및 양자 저항 보안

위의 체계는 타원 곡선에 의존하는데, 이는 양호하지만 불행하게도 양자 컴퓨터에 취약합니다. 양자 컴퓨터가 문제가 된다면 양자 저항 알고리즘으로 전환해야 합니다. 타원 곡선 상동성과 격자의 두 가지 자연 후보가 있습니다.

타원 곡선 상동성은 위에서 수행한 것과 유사한 암호화 트릭을 사용할 수 있게 해주는 선형 속성을 갖는 타원 곡선을 기반으로 하는 매우 다른 수학적 구성이지만 양자 컴퓨터에 취약할 수 있는 구성을 깔끔하게 피합니다. 이산 대수 공격의 순환 그룹 .

신원 기반 암호화의 주요 약점은 매우 복잡한 기본 수학과 이러한 복잡성 아래 숨겨진 가능한 공격의 위험입니다. 작년에 일부 동종 기반 프로토콜이 손상되었지만 다른 프로토콜은 여전히 안전합니다. 상동성의 주요 이점은 상대적으로 작은 키 크기와 많은 타원 곡선 기반 방법으로 직접 이식할 수 있는 기능입니다.

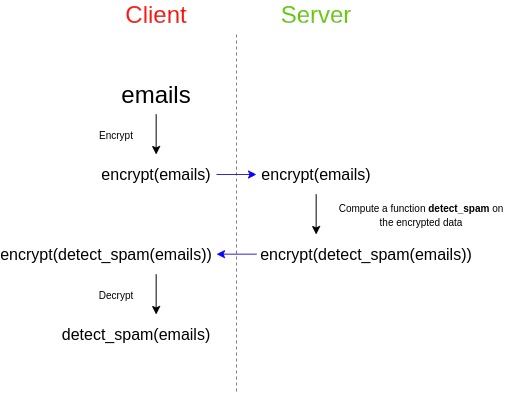
CSIDH의 3-상동성, 소스는 여기입니다.

래티스는 타원 곡선 동형사상보다 훨씬 단순한 수학에 의존하는 매우 다른 암호화 구조이며 매우 강력한 기능(예: 완전 동형 암호화(FHE))을 수행할 수 있습니다. 스텔스 주소 체계는 격자에 구축할 수 있지만 최상의 체계를 설계하는 것은 미해결 문제입니다. 그러나 격자 기반 구조는 키 크기가 더 큰 경향이 있습니다.

격자를 응용한 완전 동형암호. FHE는 또한 다른 방식으로 스텔스 주소 프로토콜을 지원하는 데 사용할 수 있습니다. 즉, Bob이 보기 키를 공개하지 않고 전체 체인에 자산이 포함되어 있는지 확인하는 스텔스 주소 계산을 아웃소싱하는 데 도움이 됩니다.

세 번째 접근 방식은 일반 블랙박스 프리미티브(많은 사람들이 다른 이유로 필요로 하는 기본 요소)에서 스텔스 주소 체계를 구축하는 것입니다. 체계의 공유 비밀 생성 부분은 공개 키 암호화 시스템의 중요한 구성 요소인 키 교환에 직접 매핑됩니다. 어려운 부분은 Alice가 스텔스 주소(지출 키 아님)만 생성하고 Bob이 지출 키를 생성하도록 하는 병렬 알고리즘입니다.

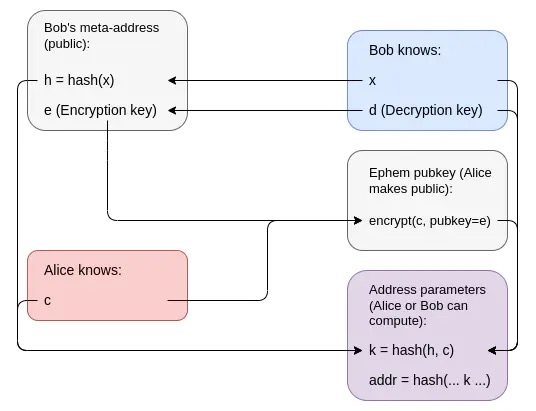
불행히도 공개 키 암호 시스템을 구축하는 데 필요한 것보다 더 간단한 요소를 사용하여 스텔스 주소를 구축할 수 없습니다. 간단한 증거가 있습니다. 은밀한 주소 체계를 사용하여 공개 키 암호화 시스템을 구축할 수 있습니다. Alice가 Bob에게 메시지를 암호화하려는 경우 그녀는 N개의 트랜잭션을 보낼 수 있으며 각 트랜잭션은 Bob의 스텔스 주소 중 하나 또는 자신의 스텔스 주소 중 하나로 전송되며 Bob은 뉴스 받기를 읽기 위해 수신한 트랜잭션을 확인할 수 있습니다. . 이는 해시만으로는 공개 키 암호화를 수행할 수 없고 해시만으로 영지식 증명을 수행할 수 있다는 수학적 증거가 있기 때문에 중요합니다. 따라서 스텔스 주소는 해시만으로 수행할 수 없습니다.

c의 암호화는 Bob에게 다른 사람에 대해 아무 것도 알려주지 않으며 k는 해시이므로 c에 대해 거의 아무것도 나타내지 않습니다. 지갑 코드 자체에는 k만 포함되며 c는 비공개이므로 k를 h까지 추적할 수 없습니다.

그러나 이것은 STARK가 필요하고 STARK는 큽니다. 궁극적으로 포스트 퀀텀 이더리움 세계에는 많은 Stark를 사용하는 많은 응용 프로그램이 포함될 가능성이 높으므로 공간을 절약하기 위해 이러한 모든 Stark를 하나의 재귀 Stark로 결합하기 위해 여기에 설명된 것과 같은 집계 프로토콜을 옹호합니다.

첫 번째 레벨 제목

스텔스 주소 및 소셜 복구 및 다중 L2 지갑

저는 오랫동안 소셜 복구 지갑의 팬이었습니다. 기관, 다른 장치 및 친구 간에 키가 공유되는 다중 서명 메커니즘이 있는 지갑입니다. 마스터 키를 잃어버렸습니다.

그러나 소셜 복구 지갑은 스텔스 주소와 잘 섞이지 않습니다. 계정을 복원해야 하는 경우(즉, 계정을 제어하는 개인 키 변경) N 스텔스 지갑의 계정 확인을 변경하기 위한 몇 가지 단계도 수행해야 합니다. 논리적으로 이것은 높은 수수료, 편의성 및 개인 정보 보호 비용을 희생하면서 N개의 트랜잭션이 필요합니다.

소셜 복구 및 여러 계층 2 프로토콜의 세계 상호 작용에 대한 유사한 우려가 있습니다. Optimism, Arbitrum, Starknet, Scroll, Polygon에 계정이 있고 이러한 롤업 중 일부는 확장 이유 인스턴스를 위해 병렬로 12개가 있을 수 있습니다. 각 인스턴스에 계정이 있으므로 키 변경은 매우 복잡한 작업이 될 수 있습니다.

여러 체인에서 여러 계정의 키를 변경하는 것은 엄청난 양의 작업입니다.

이를 통해 많은 계층 2 프로토콜에 걸쳐 많은 계정이 어딘가(기본 체인 또는 일부 계층 2)에서 k의 단일 값에 의해 제어될 수 있습니다. 여기서 하나의 값을 변경하면 모든 계정의 소유권을 변경하기에 충분합니다. 계정 간의 연결을 공개합니다.