前章に引き続き、「多要素モデルを使用した強力な暗号資産ポートフォリオの構築」に関する一連の記事を 3 回公開しました。「理論の基礎」、「データの前処理」、「因子妥当性テスト」。

最初の 3 つの記事では、多要素戦略の理論と単一要素テストの手順をそれぞれ説明します。

1. 因子相関検定の理由: 多重共線性

単一因子テストを通じて一連の有効な因子を選別しますが、上記の因子をデータベースに直接入力することはできません。要因そのものは、具体的な経済的意味に応じて大まかに分類できる 同種の要因間には強い相関関係がある 相関スクリーニングを行わずに直接データベースに入力し、重回帰を行って期待収益率を算出した場合さまざまな要因に基づいて、多重共線性の問題が発生します。計量経済学における多重共線性とは、回帰モデル内の一部またはすべての説明変数が「完全な」または正確な線形関係 (変数間の高い相関関係) を持っていることを意味します。

したがって、有効な因子を選別した後、まず大分類ごとに因子の相関関係をT検定し、相関性の高い因子については有意性の低い因子を破棄するか、因子合成を行う必要があります。

多重共線性の数学的説明は次のとおりです。

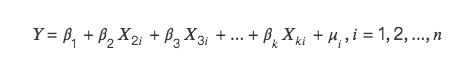
次の 2 つの状況が考えられます。

多重共線性の結果:

1. パラメータ推定器は完全な共線性の下では存在しません

2. OLS 推定器は、近似共線性の下では有効ではありません。

3. パラメータ推定量の経済的重要性は不合理である

4. 変数の有意性検定 (t 検定) は有意性を失います。

5. モデルの予測関数は失敗します。多変量線形モデルによって適合された予測収益率は非常に不正確であり、モデルは失敗します。

2. ステップ 1: 同じタイプの因子の相関検定

新しく計算された因子とデータベースにすでに存在する因子の間の相関関係をテストします。一般に、相関関係のデータには次の 2 種類があります。

1. バックテスト期間中のすべてのトークンの因子値に基づいて相関関係を計算します

2.バックテスト期間中の全トークンの因子超過戻り値に基づいて相関関係を計算

私たちが求める各要素は、トークンの収益率に一定の貢献と説明力を持っています。相関テスト**を実施する目的は、異なる説明と戦略リターンへの寄与を持つ要因を見つけることであり、戦略の最終目標はリターン**です。 2 つの因子が同じリターンを記述する場合、2 つの因子の値が大きく異なっていても意味がありません。したがって、ファクター値自体に大きな差があるファクターを見つけたかったのではなく、リターンを説明する異なるファクターを持つファクターを見つけたかったため、最終的にファクター超過リターン値を使用して相関関係を計算することにしました。

私たちの戦略は毎日の頻度であるため、バックテスト間隔の日付に基づいてファクター超過収益間の相関係数行列を計算します。

ライブラリ内で相関性が最も高い上位 n 個の因子をプログラムで解決します。

def get_n_max_corr(self, factors, n= 1):
       factors_excess = self.get_excess_returns(factors)
       save_factor_excess = self.get_excess_return(self.factor_value, self.start_date, self.end_date)
       if len(factors_excess) < 1:
           return factor_excess, 1.0, None
       factors_excess[self.factor_name] = factor_excess['excess_return']
       factors_excess = pd.concat(factors_excess, axis= 1)
       factors_excess.columns = factors_excess.columns.levels[ 0 ]
       # get corr matrix
       factor_corr = factors_excess.corr()
       factor_corr_df = factor_corr.abs().loc[self.factor_name]
       max_corr_score = factor_corr_df.sort_values(ascending=False).iloc[ 1:].head(n)
       
       return save_factor_excess, factor_corr_df, max_corr_score

3. ステップ 2: 因子の選択と因子の合成

相関性の高い因子セットの場合、それらに対処する方法が 2 つあります。

(1) 因子の選択

ファクター自体の ICIR 値、利回り、回転率、シャープ レシオに基づいて、特定の次元で最も効果的なファクターが選択されて保持され、他のファクターは削除されます。

(2) 因子合成

因子セット内の因子を合成し、断面上で可能な限り多くの有効な情報を保持します。

現在、処理すべき因子行列が 3 つあると仮定します。

2.1 均等な重み付け

各因子の重みは等しく（w=1/因子の数）、総合因子＝各因子の値の合計が平均されます。

例: モメンタム要因、1 か月収益率、2 か月収益率、3 か月収益率、6 か月収益率、12 か月収益率 これら 6 つの要因の要因負荷量は、それぞれを説明します。重量の 1/6、新しい運動量係数負荷を合成し、再度正規化を実行します。

Synthetic 1 = Synthetic.mean(axis= 1) # 行ごとに平均を求める

2.2 過去の IC 重み付け、過去の ICIR、過去の収入重み付け

ファクターは、バックテスト期間にわたる IC 値 (ICIR 値、履歴戻り値) によって重み付けされます。過去には多くの期間があり、各期間には IC 値があるため、その平均が係数の重みとして使用されます。バックテスト期間にわたる IC の平均 (算術平均) を重みとして使用するのが一般的です。

2.3 過去の IC 半減期の重み付け、過去の ICIR 半減期の重み付け

2.1 と 2.2 はどちらも算術平均を計算し、バックテスト期間の各 IC と ICIR はデフォルトで係数に同じ影響を与えます。

ただし、実際には、バックテスト期間の各期間が現在の期間に与える影響はまったく同じではなく、時間による減衰が生じます。期間が現在の期間に近づくほど影響は大きくなり、離れるほど影響は小さくなります。この原理に基づいて、IC 重みを計算する前に、まず半減期重みを定義し、現在の期間に近いほど重みの値が大きくなり、遠ざかるほど重みが小さくなります。

半減期重量の数学的導出:

2.4 ICIR 重み付けを最大化する

方程式を解くことで、ICIR を最大化する最適な因子重み w を計算します。

共分散行列推定問題: 共分散行列は、異なる資産間の相関を測定するために使用されます。統計学では母集団共分散行列の代わりに標本共分散行列がよく使われますが、標本サイズが不十分な場合、標本共分散行列と母集団共分散行列は大きく異なります。そこで、推定された共分散行列と実際の共分散行列の間の平均二乗誤差を最小化するという圧縮推定法が提案されました。

方法：

1. サンプル共分散行列

2. Ledoit-Wolf 収縮: 収縮係数を導入して元の共分散行列と単位行列を混合し、ノイズの影響を軽減します。

3. Oracle 近似収縮: Ledoit-Wolf 収縮を改良したもの。目標は、共分散行列を調整することで、サンプル サイズが小さい場合に真の共分散行列をより正確に推定することです。 (プログラミング実装は Ledoit-Wolf 収縮と同じです)

2.5 主成分分析 PCA

主成分分析 (PCA) は、次元を削減し、データの主な特徴を抽出するために使用される統計手法です。目標は、線形変換を通じて元のデータを新しい座標系にマッピングし、新しい座標系におけるデータの分散を最大化することです。

具体的には、PCA はまずデータ内の主成分を見つけます。これは、データ内で最大の分散を持つ方向です。次に、最初の主成分と直交し (無関係で)、最大の分散を持つ 2 番目の主成分を見つけます。このプロセスは、データ内のすべての主成分が見つかるまで繰り返されます。