LUCIDA:如何利用多因子策略构建强大的加密资产投资组合(因子有效性检验篇)
序文
前著に引き続き、「多要素モデルを使用した強力な暗号資産ポートフォリオの構築」に関する記事シリーズの 2 つの記事を公開しました。「理論の基礎」、「データの前処理」
今回は 3 番目の記事「因子妥当性テスト」です。
特定の因子の値を決定した後、まず因子の妥当性テストを実施し、重要性、安定性、単調性、収益率の要件を満たす因子を選別する必要があり、因子の妥当性テストは因子間の関係を分析することによって行われます。現在の期間の価値と期待収益率の関係を考慮して、要因の妥当性を判断します。主に 3 つの古典的な方法があります。
IC/IR法:IC/IR値はファクター値と期待リターンの相関係数であり、ファクター値が大きいほどパフォーマンスが良いことを示します。
T値(回帰法):T値は、当期のファクター値に対する次期の収益率を線形回帰した後の係数の有意性を反映しており、回帰係数がt検定に合格するかどうかを比較することで、寄与度を判断できます。現在の期間の因子値から次の期間の収益までの値。通常は多変量 (つまり、多因子) 回帰モデルで使用されます。
階層的バックテスト方法: 階層的バックテスト方法では、因子値に基づいてトークンを階層化し、トークンの各層の収益率を計算して因子の単調性を決定します。
1. IC/IR法
(1) IC/IRの定義
IC: 情報係数。トークンのリターンを予測する要素の能力を表します。ある期間のIC値は、当期のファクター値と次期の収益率との相関係数です。
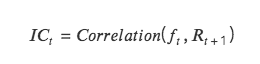

IC が 1 に近づくほど、ファクター値と次の期間の収益率の間の正の相関関係が強くなります。IC= 1 は、ファクターの通貨選択が 100% 正確であることを意味します。これは、最高のランキング スコアを持つトークンに対応します。選択されたトークンは次のポジション調整サイクルで使用されます。 、最大の増加。
ICが-1に近いほど、ファクター値と次の期間の収益率との負の相関が強くなります。IC=-1の場合、最高ランクのトークンが次の期間で最も大きく下落することを意味しますリバランス サイクル。これは完全な反転です。
IC が 0 に近い場合、そのファクターの予測能力が非常に弱いことを意味し、そのファクターがトークンに対する予測能力を持たないことを示します。
IR:情報比。因子が安定したアルファを取得する能力を表します。 IR は、すべての期間の平均 IC をすべての期間の IC 標準偏差で割ったものです。
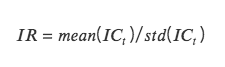
IC の絶対値が 0.05 (0.02) より大きい場合、ファクターの銘柄選択能力は強力です。 IRが0.5より大きい場合、安定して超過収益を得る能力が高いファクターとなります。
(2)ICの計算方法
標準 IC (ピアソン相関): 最も古典的な相関係数であるピアソン相関係数を計算します。ただし、この計算方法には多くの前提条件があります。データは連続的で正規分布し、2 つの変数は線形関係を満たすなどです。
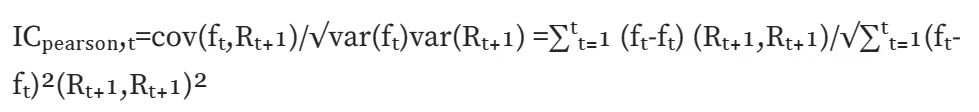
ランク IC (スピアマンの順位相関係数): スピアマンの順位相関係数を計算し、最初に 2 つの変数を並べ替えてから、並べ替えた結果に基づいてピアソン相関係数を計算します。スピアマンの順位相関係数は 2 つの変数間の単調な関係を評価し、順序付けされた値に変換されるため、データの外れ値の影響をあまり受けません。ピアソン相関係数は、2 つの変数間の線形関係を評価します。これは、元のデータに対する特定の前提条件があるだけでなく、データの外れ値によっても大きく影響されます。実際の計算では、ランク IC を見つける方がより一貫性があります。
(3) IC/IRメソッドのコード実装
日付と時刻の昇順で一意の日付と時刻の値のリストを作成します - リバランス日を記録します defchoosedate(dateList,cycle)
class TestAlpha(object):
def __init__(self, ini_data):
self.ini_data = ini_data
def chooseDate(self, cycle, start_date, end_date):
'''
cycle: day, month, quarter, year
df: 元のデータフレーム df、日付列の処理
'''
chooseDate = []
dateList = sorted(self.ini_data[self.ini_data['date'].between(start_date, end_date)]['date'].drop_duplicates().values)
dateList = pd.to_datetime(dateList)
for i in range(len(dateList)-1):
if getattr(dateList[i], cycle) != getattr(dateList[i + 1 ], cycle):
chooseDate.append(dateList[i])
chooseDate.append(dateList[-1 ])
chooseDate = [date.strftime('%Y-%m-%d') for date in chooseDate]
return chooseDate
def ICIR(self, chooseDate, factor):
#1. まず各位置調整日のIC、つまりICtを表示します。
testIC = pd.DataFrame(index=chooseDate, columns=['normalIC','rankIC'])
dfFactor = self.ini_data[self.ini_data['date'].isin(chooseDate)][['date','name','price', factor]]
for i in range(len(chooseDate)-1):
# ( 1) normalIC
X = dfFactor[dfFactor['date'] == chooseDate[i]][['date','name','price', factor]].rename(columns={'price':'close 0'})
Y = pd.merge(X, dfFactor[dfFactor['date'] == chooseDate[i+ 1 ]][['date','name','price']], on=['name']).rename(columns={'price':'close 1'})
Y['returnM'] = (Y['close 1'] - Y['close 0']) / Y['close 0']
Yt = np.array(Y['returnM'])
Xt = np.array(Y[factor])
Y_mean = Y['returnM'].mean()
X_mean = Y[factor].mean()
num = np.sum((Xt-X_mean)*(Yt-Y_mean))
den = np.sqrt(np.sum((Xt-X_mean)** 2)*np.sum((Yt-Y_mean)** 2))
normalIC = num / den # pearson correlation
# ( 2) rankIC
Yr = Y['returnM'].rank()
Xr = Y[factor].rank()
rankIC = Yr.corr(Xr)
testIC.iloc[i] = normalIC, rankIC
testIC =testIC[:-1 ]
# 2. ICt に基づいて、[IC_Mean, IC_Std,IR,IC を見つけます<0 比率 - 因子の方向、-IC ->0.05 比率]
'''
ICmean: |IC|>0.05,ファクターはコインを選択する能力が強く、ファクターの値は次の期間の収益率と高い相関を持っています。 -IC-<0.05,ファクターの通貨選択能力が弱く、ファクター値と次期収益率との相関性が低い。
IR: |IR|>0.5,ファクター通貨選択力が強く、IC価値も比較的安定しています。 -IR-<0.5,IR 値が小さすぎるため、この係数はあまり効果的ではありません。 0に近い場合は基本的に無効となります。
IClZero (IC がゼロ未満): IC<0 がほぼ半分を占めます -> ファクター ニュートラル、IC>0 が半分を超え、マイナスのファクターです。つまり、ファクター値が増加するにつれて、収益率が低下します。
ICALzpF(IC abs large than zero poin five): |IC|>0.05 という比率は高い方にあり、ほとんどの要素が有効であることを示しています。
'''
IR = testIC.mean()/testIC.std()
IClZero = testIC[testIC<0 ].count()/testIC.count()
ICALzpF = testIC[abs(testIC)>0.05 ].count()/testIC.count()
combined =pd.concat([testIC.mean(), testIC.std(), IR, IClZero, ICALzpF], axis= 1)
combined.columns = ['ICmean','ICstd','IR','IClZero','ICALzpF']
#3.リバランス期間中のIC累積チャート
print("Test IC Table:")
print(testIC)
print("Result:")
print('normal Skewness:', combined['normalIC'].skew(),'rank Skewness:', combined['rankIC'].skew())
print('normal Skewness:', combined['normalIC'].kurt(),'rank Skewness:', combined['rankIC'].kurt())
return combined, testIC.cumsum().plot()
2. T値検定(回帰法)
T 値法でも、当期のファクター値と次期の収益率の関係をテストしますが、両者の相関関係を分析する点で ICIR 法とは異なります。従属変数 Y として戻り、現在の期間の因子値を独立変数 X として返します。X 回帰の場合、回帰因子値の回帰係数に対して t 検定を実行して、回帰因子値が 0 から有意に異なるかどうか、つまり、現在の期間の要因は、次の期間の返品率に影響します。
この手法の本質は二変量回帰モデルを解くことであり、具体的な式は次のとおりです。
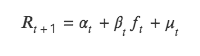

(1) 回帰法の理論

(2) 回帰手法のコード実装
def regT(self, chooseDate, factor, return_ 24 h):
testT = pd.DataFrame(index=chooseDate, columns=['coef','T'])
for i in range(len(chooseDate)-1):
X = self.ini_data[self.ini_data['date'] == chooseDate[i]][factor].values
Y = self.ini_data[self.ini_data['date'] == chooseDate[i+ 1 ]][return_ 24 h].values
b, intc = np.polyfit(X, Y,1) # 勾配
ut = Y - (b * X + intc)
# t 値を求める t = (\hat{b} - b) / se(b)
n = len(X)
dof = n - 2 # 自由度
std_b = np.sqrt(np.sum(ut** 2) / dof)
t_stat = b / std_b
testT.iloc[i] = b, t_stat
testT = testT[:-1 ]
testT_mean = testT['T'].abs().mean()
testT L1 96 = len(testT[testT['T'].abs() > 1.96 ]) / len(testT)
print('testT_mean:', testT_mean)
print(1.96を超えるT値の割合:, testT L1 96)
return testT
3. 層別バックテスト手法
層化とはすべてのトークンを層化することを指し、バックテストはトークンの組み合わせの各層の収益率を計算することを指します。
(1) 階層化
まず、トークン プールに対応するファクター値を取得し、そのファクター値でトークンを並べ替えます。昇順に並べ替えます。つまり、係数値が小さいものが最初にランク付けされ、並べ替えに従ってトークンが均等に分割されます。レイヤ 0 トークンのファクタ値が最も小さく、レイヤ 9 トークンのファクタ値が最も大きくなります。
理論的には、「均等分割」とは、トークンの数を均等に分割すること、つまり、各レイヤーのトークンの数が同じであることを指します。これは分位数を使用して実現されます。実際には、トークンの総数は必ずしもレイヤー数の倍数であるとは限りません。つまり、各レイヤーのトークンの数は必ずしも等しいとは限りません。
(2) バックテスト
因子値の小さい順にトークンを10グループに分けた後、各トークンの組み合わせの還元率の計算を開始します。このステップでは、各レイヤーのトークンを投資ポートフォリオとして扱い(各レイヤーのトークンの組み合わせに含まれるトークンは、異なるバックテスト期間中に変化します)、ポートフォリオの全体的な価値を計算します。次期収益率。 ICIR と t 値は現在の係数値を分析し、次期の全体収益率ただし、段階的なバックテストには計算が必要ですバックテスト期間中の各営業日の層別ポートフォリオ収益率。バックテストは期間が多いため、期間ごとに層別化とバックテストが必要になります。最後に、各レイヤーのトークン還元率を累積的に乗算して、トークンの組み合わせの累積還元率を計算します。
理想的には、良好なファクターの場合、グループ 9 のカーブ リターンが最も高く、グループ 0 のカーブ リターンが最も低くなります。
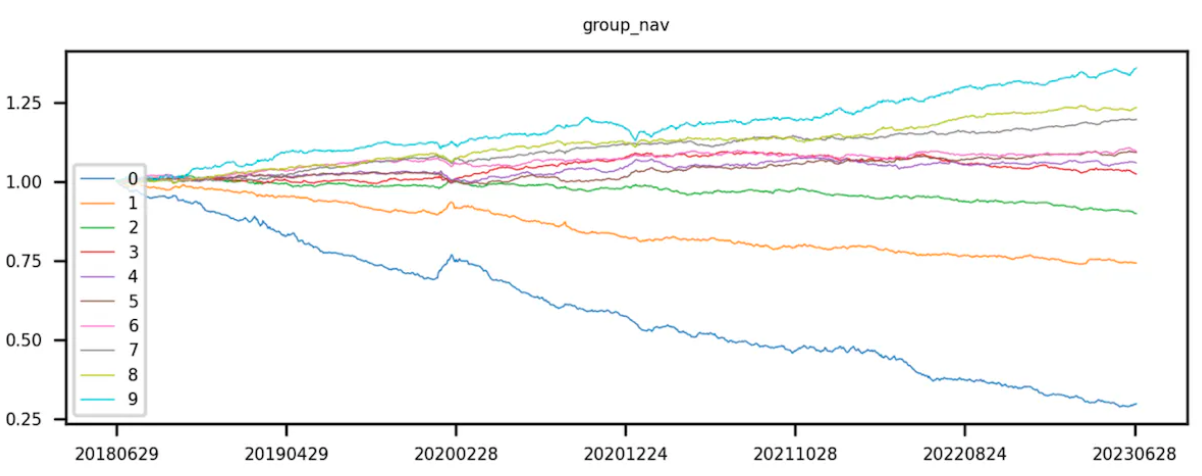
グループ 9 からグループ 0 を引いた曲線 (つまり、ロングとショートのリターン) は単調増加しています。
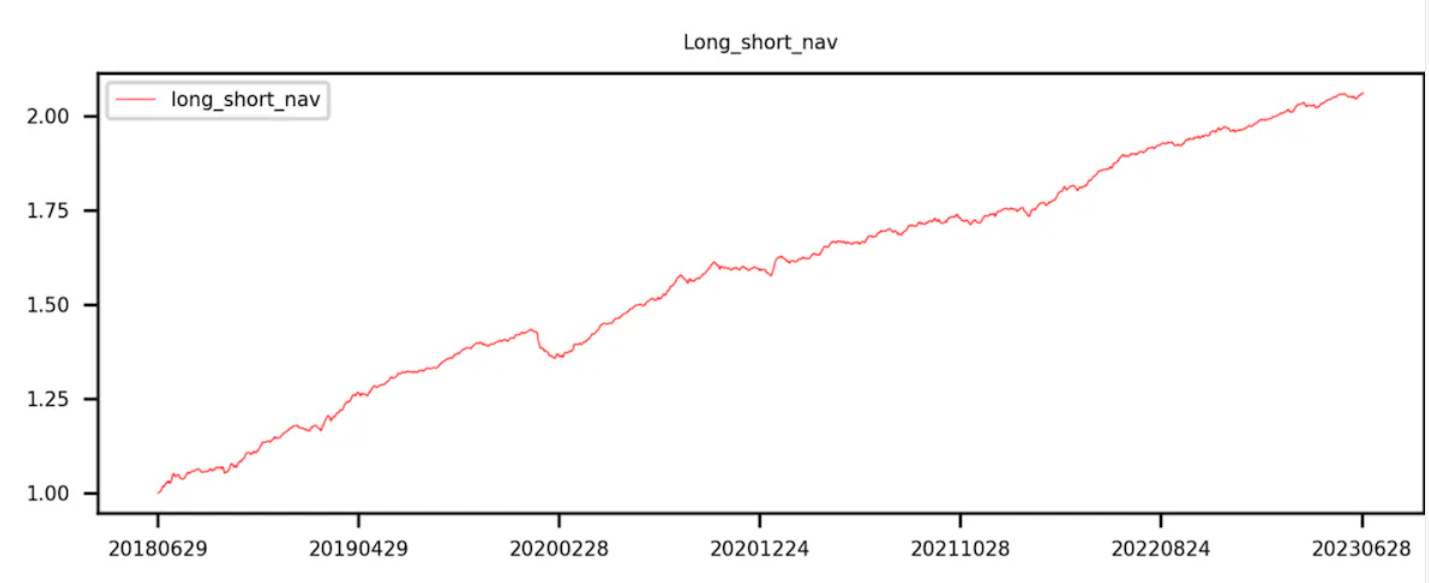
(3) 階層型バックテスト手法のコード実装
def layBackTest(self, chooseDate, factor):
f = {}
returnM = {}
for i in range(len(chooseDate)-1):
df 1 = self.ini_data[self.ini_data['date'] == chooseDate[i]].rename(columns={'price':'close 0'})
Y = pd.merge(df 1, self.ini_data[self.ini_data['date'] == chooseDate[i+ 1 ]][['date','name','price']], left_on=['name'], right_on=['name']).rename(columns={'price':'close 1'})
f[i] = Y[factor]
returnM[i] = Y['close 1'] / Y['close 0'] -1
labels = ['0','1','2','3','4','5','6','7','8','9']
res = pd.DataFrame(index=['0','1','2','3','4','5','6','7','8','9','LongShort'])
res[chooseDate[ 0 ]] = 1
for i in range(len(chooseDate)-1):
dfM = pd.DataFrame({'factor':f[i],'returnM':returnM[i]})
dfM['group'] = pd.qcut(dfM['factor'], 10, labels=labels)
dfGM = dfM.groupby('group').mean()[['returnM']]
dfGM.loc[LongShort] = dfGM.loc[0]- dfGM.loc[9]res[chooseDate[i+ 1 ]] = res[chooseDate[ 0 ]] * ( 1 + dfGM[returnM ]) data = pd.DataFrame({階層型累積収益:res.iloc[: 10,-1],Group:[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9]})
df 3 = data.corr()
print("Correlation Matrix:")
print(df 3)
return res.T.plot(title='Group backtest net worth curve')



