原作者：Vitalik Buterin

原作者：

• 現在のデータ可用性サンプリング (DA サンプリングまたは DAS) スキームは、KZG コミットメントを使用して行われます。 KZG Promise の利点は、非常に使いやすく、非常に優れた代数的特性を備えていることです。

• 評価証明は一定のサイズを持ち、一定の時間で検証できます。

• ここには、単位の N 個の根のそれぞれで deg を評価するすべての証明を O(N∗log(N)) 時間で計算するアルゴリズムが存在します。

• コミットメントを線形結合して、コミットメントの線形結合を取得できます: com(P)+com(Q)=com(P+Q)

証明を線形に組み合わせることができます: Proof(P,x)+Proof(Q,x)+Proof(P+Q,x)

1 つ目のポイントは、優れた効率の保証です。 2 番目のポイントは、DA サンプリングの準備ができた BLOB を簡単に生成できることを保証します。すべての証明を生成するのにこれだけ O(N2) かかる場合、DAS 対応にするために高度に集中化されたアクターまたは複雑な分散アルゴリズムが必要になります。

• 3 番目と 4 番目のポイントは 2D サンプリングにとって非常に価値があり、分散ブロックプロデューサーと効率的な自己修復を可能にします。

• ブロックプロデューサーは、FFT-over-the-curve を使用して「列を拡張」し、

行ごとの再構築を行うだけでなく、列ごとの再構築も行うことができます。列の一部の値と証明が欠落している場合 (ただし半分以上はまだ利用可能)、FFT を実行してデータを回復できます。欠損値と証明。ただし、KZG には弱点があります。それは、複雑なペアリング暗号化と信頼できる設定に依存しているということです。ペア暗号化は 20 年以上にわたって研究され、使用されてきました。信頼できる設定は N で 1 つの信頼仮定です。N は数百人の参加者であるため、実際のリスクは高く、著者らは KZG の使用を継続することは完全に許容できると感じています。ただし、次のような質問をする価値はあります。

KZG のコストを支払いたくない場合、代わりに内積パラメータ (IPA) を使用できますか?

IPA の説明については、この記事の前半を参照してください。

• IPA には次の特性があります。

• 評価は対数サイズであることが判明し、線形時間 (サイズ 4096 の多項式の場合約 40 ミリ秒) で検証できます。

• 効率的なマルチプルーフ生成アルゴリズムは知られていません。

• コミットメントは楕円曲線の点であり、KZG コミットメントのように直線的に結合できます。

線形結合を証明する既知の方法はありません。

したがって、いくつかの資産を保持し、いくつかを失います。実際、私たちは証拠を生成、配布、自己修復する「現在の方法」がもはや不可能になるほど多くのものを失いました。この投稿では、少し不格好ではありますが、目的を達成できる代替方法について説明します。

代替案

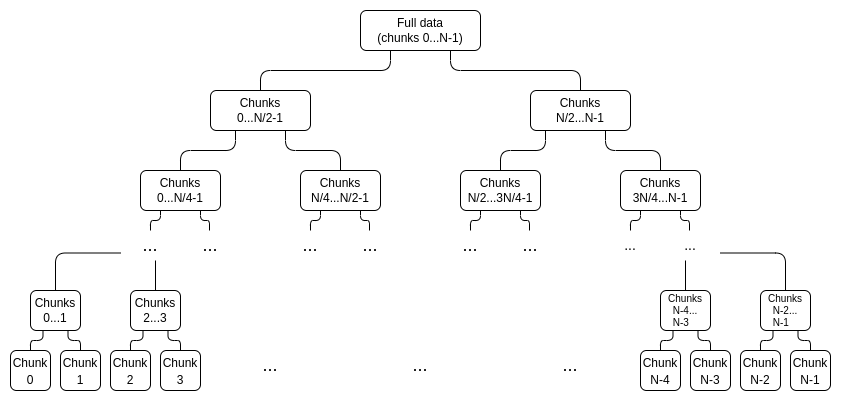
まず、deg の代わりに証明木を生成します。

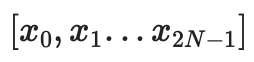
データを評価形式で解釈し、ベクトルとして扱います。

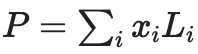
, ここで、多項式は

(Li は、セット内の座標 i で 1、その他の座標 0 に等しい deg<2N 多項式です)。

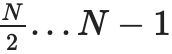
証明ツリーの各ノードは、データのその部分に対するコミットメントであり、このコミットメントが実際に「範囲内」にあることの証明です。例えば、

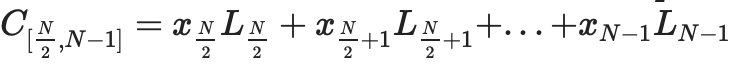
ノードにはPromiseが含まれます

。 IPA証明書が発行されますので、

実際には、これらの点の線形結合であり、他の点は結合しません。

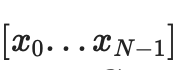
2 つのツリーを生成します。最初のツリーは

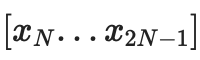
、2番目の
、データに対する「完全な」コミットメントは、C[0,N−1] と C[N,2N−1] で構成されます。

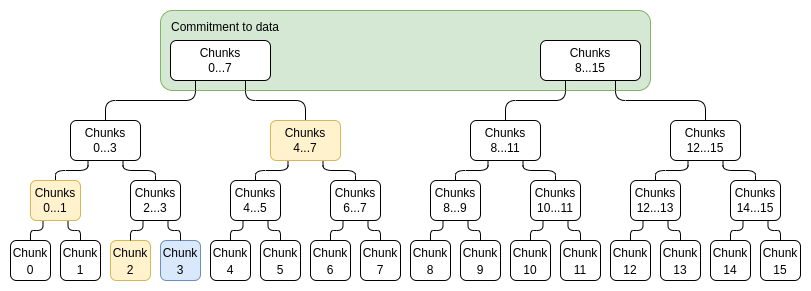
特定の値 xi を証明するには、0...N−1 または N....2N−1 (i を含む方)、i を含まない範囲全体をカバーする (サブコミットメント、証明) ペアのリストを提供するだけです。私が属していないトップレベルのコミットは、正しい構築の証拠です。たとえば、N=8 および i=3 の場合、証明には C[0,1]、C2、C[4,7] とその証明、および C[8,15] が正しく構築されたことの証明が含まれます。証明は、個々の証明を検証し、コミットメントの合計が完全なコミットメントに達することを確認することによって検証されます。

青: チャンク 3、黄色: チャンク 3 の証拠。

効率を高めるために各チャンクが単一の評価である必要はないことに注意してください。代わりに、チャンクが 16 個の評価のセットになるようにツリーを枝刈りできます。いずれにせよ、証明の合計サイズがこれよりも大きくなることを考えると、このようにチャンクを大きくしても損失はほとんどありません。

これらの証明の生成には O(N*log(N)) 時間がかかります。証明の検証には O(N) 時間かかりますが、多くの証明はバッチで検証できることに注意してください。IPA を検証する O(N) ステップは楕円曲線線形結合であり、その多くはランダムな線形結合を使用してチェックできます。各証明には依然として O(N) フィールド操作が必要ですが、これにかかる時間は 1 ミリ秒未満です。

拡張: ファンアウト (ファンアウト) が 2 より大きい

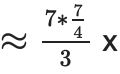
ステップごとに 2 つのファンアウトを持つ代わりに、より高いファンアウト、たとえば 8 つのファンアウトを持つことができます。コミットメントごとに 1 つのプルーフの代わりに、コミットメントごとに 7 つのプルーフが存在します。たとえば、最下層には証明 {1,2,3,4,5,6,7}、{0,2,3,4,5,6,7}、{0,1,3 があります。 、4、5、6、7}など。これにより、プルーフ生成作業の合計が次のように増加します。

(ノードごとに 7 つのプルーフ、各プルーフ サイズは元のサイズの 1.75 倍ですが、レイヤーが 3 分の 1 であるため、最大 4.08 倍の労力がかかります)、ただし、プルーフ サイズは 3 倍削減されます。

プルーフサイズ

サイズ 32 の N=128 チャンク (つまり、多項式が deg < 4096) とファンアウト (4x、4x、8x) を扱っているとします。 1 つの分岐証明には 3 つの IPA が含まれ、合計サイズは 2*(7+9+12)=56 曲線ポイント (約 1792 バイト) とチャンクの 512 バイトです。現在、256 バイトまたは 512 バイトのチャンクには 48 バイトの証明があります。

プルーフを生成するには、合計 2*8192*(3*2+7) の曲線乗算 (2 つのファンアウト 4 レイヤーの場合は 3*2、ファンアウト 8 レイヤーの場合は 7)、または合計で ~212992 の乗算が必要です。したがって、これは強力なコンピュータ (通常のコンピュータは乗算を約 50 マイクロ秒で実行できるため、これには 10 秒かかります。これは少し長すぎます)、または異なるノードが異なるチャンクに特化する分散プロセスによって迅速に実行される必要があります。

証明はバッチで検証でき、楕円曲線の乗算は 1 つだけ実行されるため、証明の検証は簡単です。したがって、KZG 証明を使用するよりもそれほど遅くならないはずです。

自己修復

列ごとに効果的に自己修復することができません。しかし、単一の修正ですべてのデータ (すべての 2M 多項式からのすべての 2N チャンク) を取得する必要を回避できるでしょうか?

1 つの行が完全に失われたと仮定します。任意の列を使用して、その列の欠落している行の値を再構築するのは簡単です。しかし、それをどうやって証明するのでしょうか？

最も単純な手法は暗号経済学です。誰でも簡単に価値を主張する債券を発行することができ、その後誰かがその主張を別の価値を証明する分岐証明とともに使用してバリデーターを打ち切ることができます。十分な正当な請求が利用可能である限り、銀行のサブネット上の誰かが請求をまとめてコミットメントと証明を再構築できます。バリデーターは、割り当てられたサンプルインデックスに対してそのようなクレームを発行することを要求される場合もあります。暗号経済学を持たないが、技術的により複雑で遅い代替方法は、正しい検証の証明とともに、その列に沿った値の M 分岐証明を渡すことです。。