foreword

foreword

The zero-knowledge proof technology in cryptography has a wide range of applications in the web3 world, including private computing, zkRollup, and so on. Among them, FOAKS used by the Layer 2 project FOX is a zero-knowledge proof algorithm. Among the above-mentioned series of applications, two attributes are extremely important for the zero-knowledge proof algorithm, that is, the efficiency and interactivity of the algorithm.

The importance of algorithm efficiency is self-evident. Efficient algorithms can significantly reduce system runtime, thereby reducing client latency and significantly improving user experience and efficiency. This is also an important reason why FOAKS is committed to achieving linear proof time.

On the other hand, from the perspective of cryptography, the design of zero-knowledge proof systems often relies on multiple rounds of interaction between the prover and the verifier. For example, in the "Zero-Knowledge Cave" story that is used in many popular science articles introducing zero-knowledge proofs, the realization of the proof depends on multiple rounds of information transmission and interaction between Alibaba (the prover) and the reporter (the verifier). But in fact, in many application scenarios, relying on interaction will make the system no longer available, or greatly increase the delay. Just like in the zkRollup system, we expect the prover (that is, the folder in FOX) to be able to calculate the correct proof value locally without depending on the interaction with the verifier.

first level title

Challenge in Zero Knowledge Proof

The zero-knowledge proof algorithm has become extremely popular with the spread of applications. In recent years, various algorithms including FOAKS, Orion, and zk-stark have also been born. The core proof logic of these algorithms, as well as the early sigma protocol in the field of cryptography, is that the prover (Prover) first sends a certain value to the verifier (Verifier), and the verifier generates a challenge (Challenge) through a local random number. The randomly generated challenge value is sent to the prover, and the prover needs to have real knowledge to respond with a high probability of passing the verifier. For example, in the zero-knowledge cave, the reporter tossed a coin and told Alibaba to come out from the left or the right. The "left and right" here is a challenge to Alibaba. Go out in the required direction, otherwise there will be half the probability of failure.

Here we notice that the generation of Challenge is a critical step, it has two requirements, random and unpredictable by the prover. First, randomness guarantees its probabilistic properties. The second point is that if the prover can predict the challenge value, it means that the security of the protocol is broken. The prover can pass the verification without knowledge. The analogy can be continued. If Alibaba can predict which side the reporter asks him to come out from, he will Even if there is no spell, you can enter that side in advance, and the results show that you can pass the agreement.

first level title

Hash Function

The name of the hash function may not be unfamiliar to us. Whether it is the mathematical problem of mining in the Bitcoin consensus protocol POW, or compressing the amount of data, constructing message verification codes, etc., there are hash functions. . Among the different protocols mentioned above, various properties of the hash function are actually used.

Specifically, the properties of a secure hash function include the following:

Compressibility: A deterministic hash function can compress a message of any length into a fixed length.

Efficiency: Given an input x, it is easy to compute the output h(x).

Anti-collision: Given an input x 1 , it is difficult to find another input x 2 , x 1 x 2 , h(x 1 ) = h(x 2 ).

Note that if the hash function satisfies collision resistance, it must satisfy one-way property, that is to say, given an output y, it is difficult to find x satisfying h(x) = y. In cryptography, it is impossible to construct a function that absolutely satisfies the one-way property in theory, but the hash function can basically be regarded as a one-way function in practical applications.

first level title

Fiat-Shamir Heuristic (Heuristic)

In fact, the Fiat-Shamir heuristic (Heuristic) is to use the hash function to hash the previously generated script to obtain a value, which is used as the challenge value.

image description

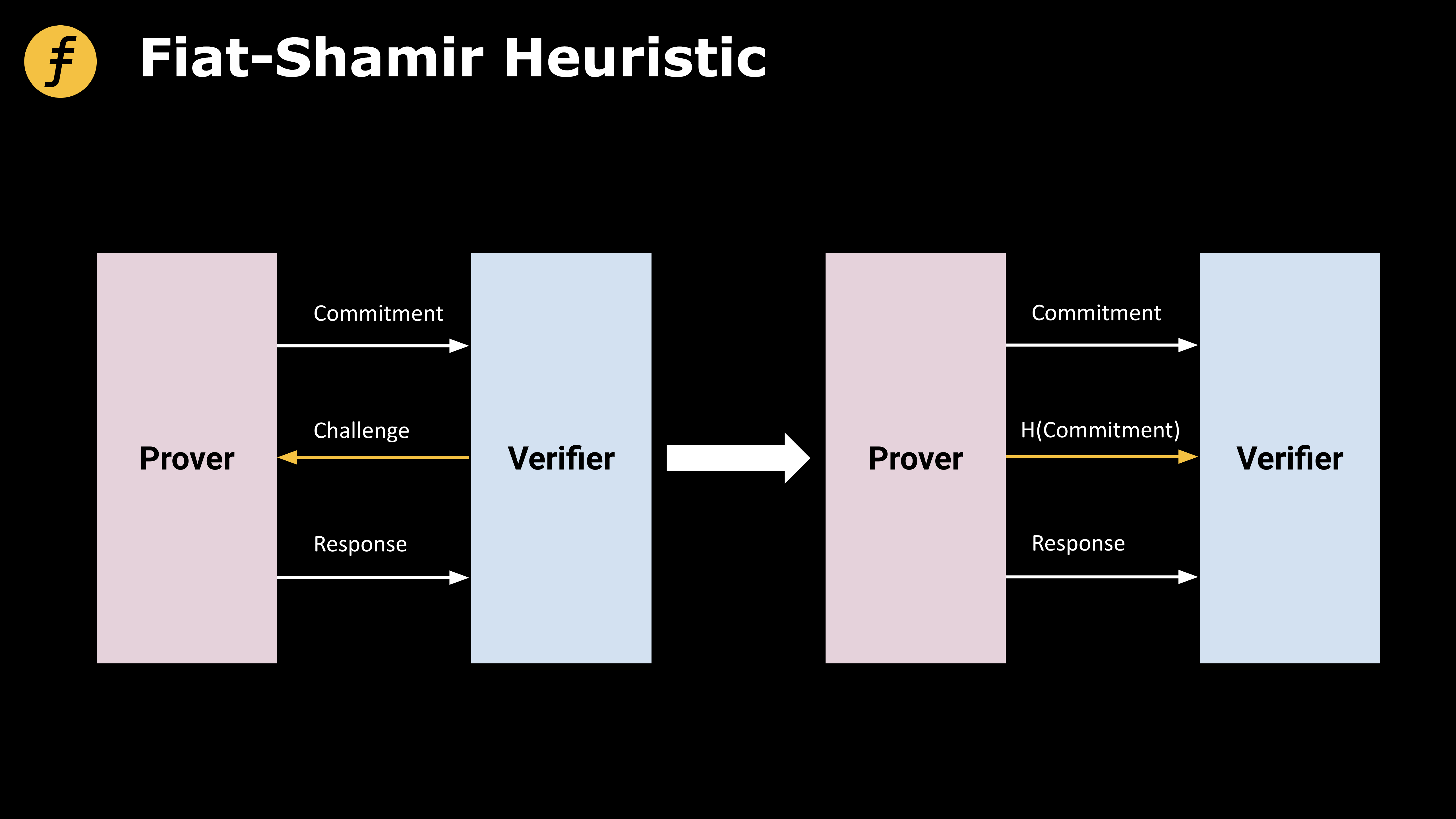
first level title

non-interactive FOAKS

In this section, we specifically demonstrate the application of the Fiat-Shamir heuristic in the FOAKS protocol, which is mainly used to generate challenges in the Brakedown part, thereby realizing non-interactive FOAKS.

image description

Figure 2: Brakedown Checks in non-interactive proof FOAKS

Now we use a hash function and let the prover generate this random vector himself.

Let γ0 =H(C1 , R, r0 , r1 ), correspondingly, in the verification calculation of the verifier, this step of calculating γ0 also needs to be added. According to this structure, it can be found that before the commitment is generated, the prover cannot predict the challenge value in advance, so it cannot "cheat" correspondingly according to the challenge value in advance, that is, correspondingly generate a false commitment value. At the same time, according to the hash The randomness of the function output, the challenge value also satisfies the randomness.

For the second point, let Î =H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 ).

epilogue

1. function PC. Commit(ϕ)：

2. Parse was a k × k matrix. The prover locally computes the tensor code encoding C1 ，C2  ，C1  is a k × n matrix，C2  is a n × n matrix.

3. for i ∈ [n] do

4. Compute the Merkle tree root Roott=Merkle.Commit(C2 [:, i])

5. Compute a Merkle tree root R=Merkle.Commit([Root0 ,......Rootn-1 ]), and output R as the commitment.

6. function PC. Prover(ϕ, X, R)

7. The prover generates a random vector γ0  ∈ Fk by computing: γ0 =H(C1 , R, r0 , r1 )

8. Proximity:

   

   
   

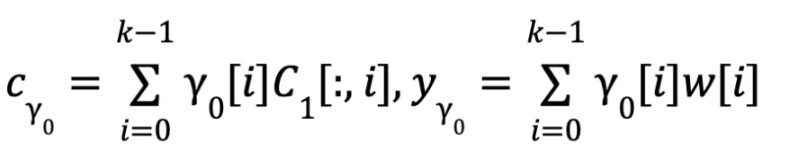
9. Consistency:

   

   
   

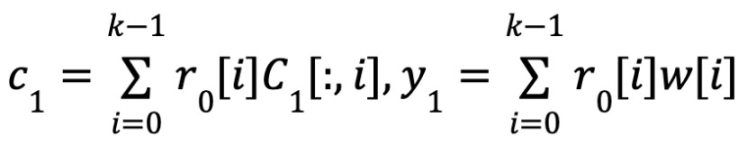
10. Prover sends c1 , y1 , cγ 0 , yγ 0  to the verifier.

11. Prover computes a vector Î as challenge, in which Î = H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 )

12. for idx ∈ Î do

13. Prover sends C1  [:, idx] and the Merkle tree proof of Rootidx for C2  [:, idx] under R to verifier

14. function PC. VERIFY_EVAL(ΠX, X, y= ϕ (X), R)

15. Proximity: ∀idx ∈ Î, Cγ 0 [idx] == <γ0 , C1 [:, idx]> and Ec(yγ 0 ) == Cγ 0 

16. Consistency: ∀idx ∈ Î, C1  [idx] == <γ0 , C1 [:, idx]> and Ec(y1 ) == C1 

17. y==

18. ∀idx ∈ Î, Ec ( C1 [:, idx]) is consistent with ROOTidx, and ROOTidx’s Merkle tree proof is valid.

19. Output accept if all conditions above holds. Otherwise output reject.

epilogue

references

references

1.Fiat, Amos; Shamir, Adi ( 1987). "How To Prove Yourself: Practical Solutions to Identification and Signature Problems". Advances in Cryptology — CRYPTO' 86. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 263: 186 – 194. doi: 10.1007/3-540-47721-7 _ 12. ISBN 978-3-540-18047-0.

2.https://www.cnblogs.com/zhuowangy 2 k/p/12246575.html