Original text author: Fox Tech CEO Kang Shuiyue, Fox Tech Chief Scientist Meng Xuanji

Original text author: Fox Tech CEO Kang Shuiyue, Fox Tech Chief Scientist Meng Xuanji

With the spread of concepts such as Bitcoin, blockchain, and smart contracts, more and more people are paying attention to the vigorous development of the Web3 field. In terms of technology, many developers also pay attention to the cryptographic protocols that support the underlying blockchain. Among them, the zero-knowledge proof protocol shines with its unique characteristics, and it plays a key role in realizing privacy protection and in the zkrollup project that realizes Layer 2 performance expansion.

Zero-knowledge proof is a general term for a class of algorithms. So far, researchers have invented many protocols including Plonk, Groth 16, zkStark, Virgo, Orion, Foaks, etc. Different protocols are suitable for different computing scenarios, and the complexity and efficiency are also different. For example, Foaks has the advantages of linear proof time and small proof length.

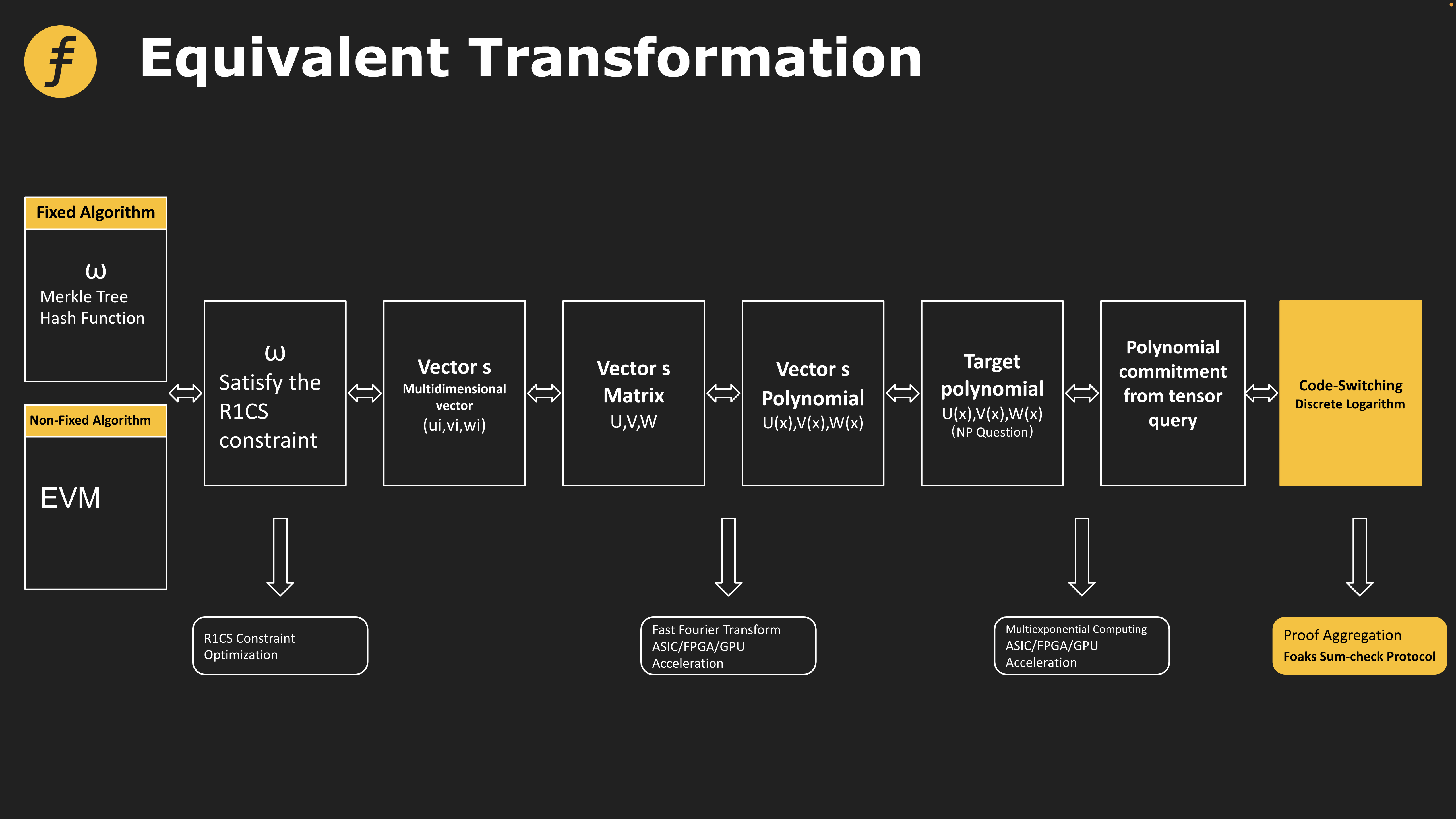
This protocol also plays an important role in the Foaks proof system adopted by Fox Tech. Specifically, in order to prove the correctness of an opcode, it is necessary to convert it into an arithmetic circuit first, then convert it into a matrix, and finally generate a polynomial, apply the algorithm in the proof system to the polynomial, and compress the part of the proof at the end Among them, the interactive process between the prover (Prover) and the verifier (Verifier) ​​is also converted into the process of calculating a certain sum, that is, the process of sum-check protocol.

first level title

Sum-check Protocol

secondary title

1. Protocol Objectives

The goal of the protocol is very simple and easy to understand.

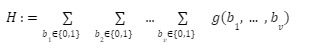
Similar to the "outsourced calculation" scenario considered in zkRollup, in the application, the calculation amount of the above formula will be very large. We hope to hand over the calculation of this formula to the prover (Prover), and then the prover will report to the verifier (Verifier) ​​to prove that their calculation results are correct.

secondary title

2. Protocol Assumptions

First of all, it is necessary to clarify the capabilities of the verifier in this protocol. We assume that the verifier has an oracle (Oracle) that can compute the function g. That is, it is easy for the verifier to compute g(r 1, ... , rv) after determining some input r 1, ... , rv. But computing the full result H is difficult.

The second point, regarding the goal of the protocol, in fact the sum-check protocol can calculate bBmg(b) for any set B, but without loss of generality, we assume B={0, 1}.

secondary title

3. Protocol process

The agreement contains a total of v rounds. One variable in g is processed in each round.

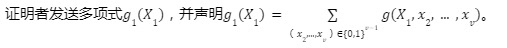
Round 1:

If the prover is honest, H=g 1( 0)+g 1( 1) should be established. The verifier verifies, and if it passes, the random number r 1 is selected and sent to the certifier. Note that, according to the assumptions of the protocol, the prover can complete the above verification.

We use degi(p) to denote the degree of the ith variable in the multivariate polynomial p. The degree of g 1(X 1) is deg 1(g), so we know that g 1 can be represented by deg 1(g)+ 1 domain elements.

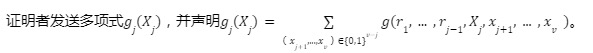
Round j (j>1):

Round v:

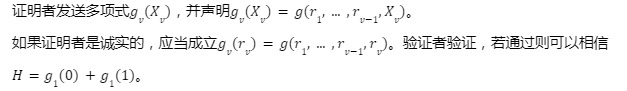
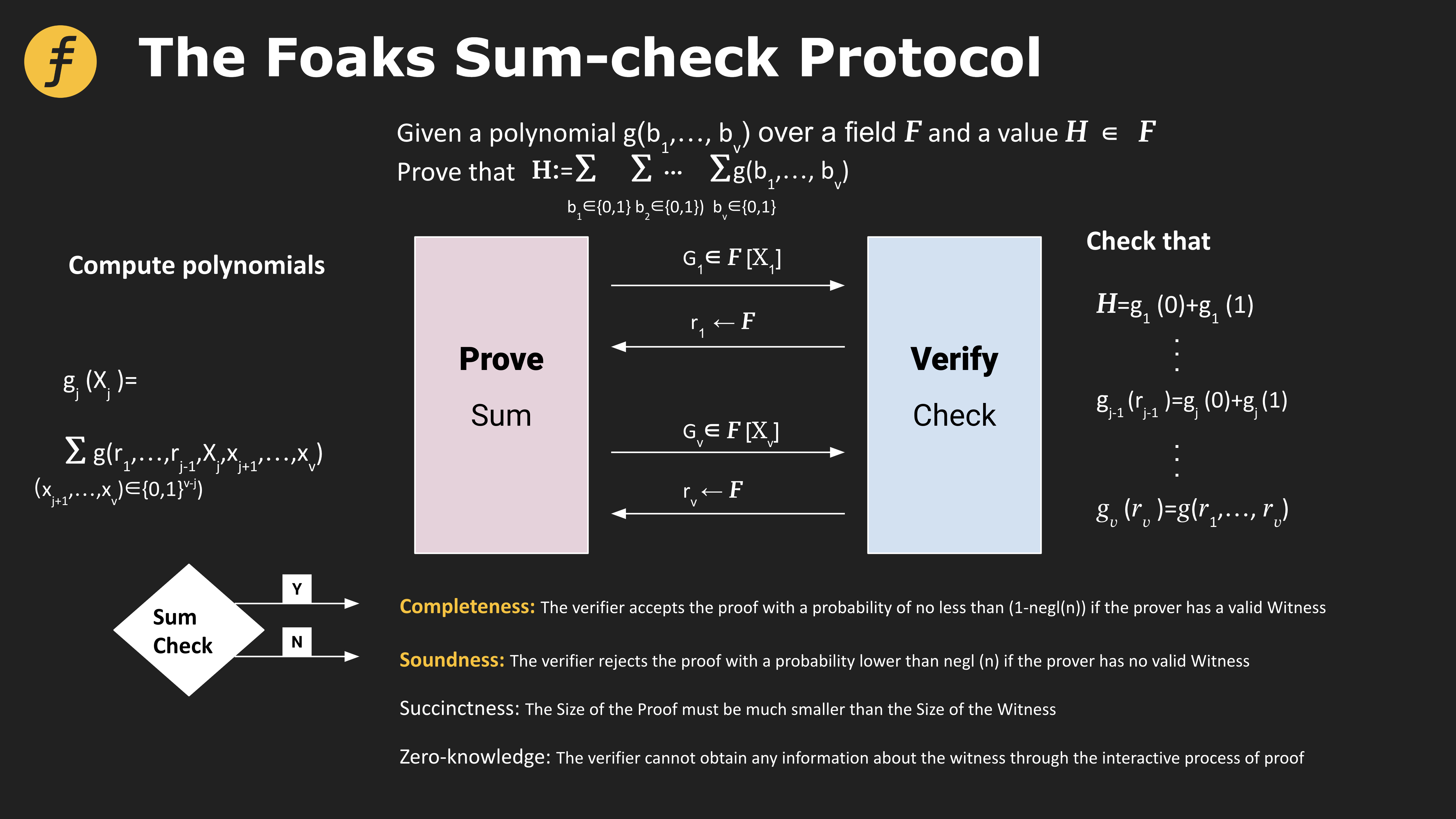
image description

• Figure 2: The Foaks Sum-check protocol

• Completeness: If the prover has a valid Witness, the verifier will accept the proof with a probability not lower than (1-negl(n));

• Soundness: If the prover does not have a valid Witness, the verifier will reject the proof with a probability lower than negl(n)

• Succinctness: The Size of Proof must be much smaller than the Size of Witness;

# where negl(n) is any negligible function

secondary title

4. Protocol complexity

The following table shows the complexity results in detail, where T represents the overhead required to access an oracle (Oracle), that is, to evaluate g once.

Figure 3: Complexity of the Sum-check protocol

first level title

Application of Sum-check Protocol

Among many zero-knowledge proof algorithms, sum-check protocol is playing an important role. The proof of many problems relies on converting the original problem into a sum-check form, and then completing the subsequent steps.

For example, the sum-check protocol can be used to count the number of triangles in an undirected graph.

First, we use the adjacency matrix A to represent the undirected graph G, let E be its edge set, then Ai, j= 1(i, j)E, that is to say, if there is an edge between points i, j then Ai, j = 1 otherwise 0. For points i, j, k, the condition for three points to form a triangle is Ai, j= 1, Ai, k= 1, Aj, k= 1 .

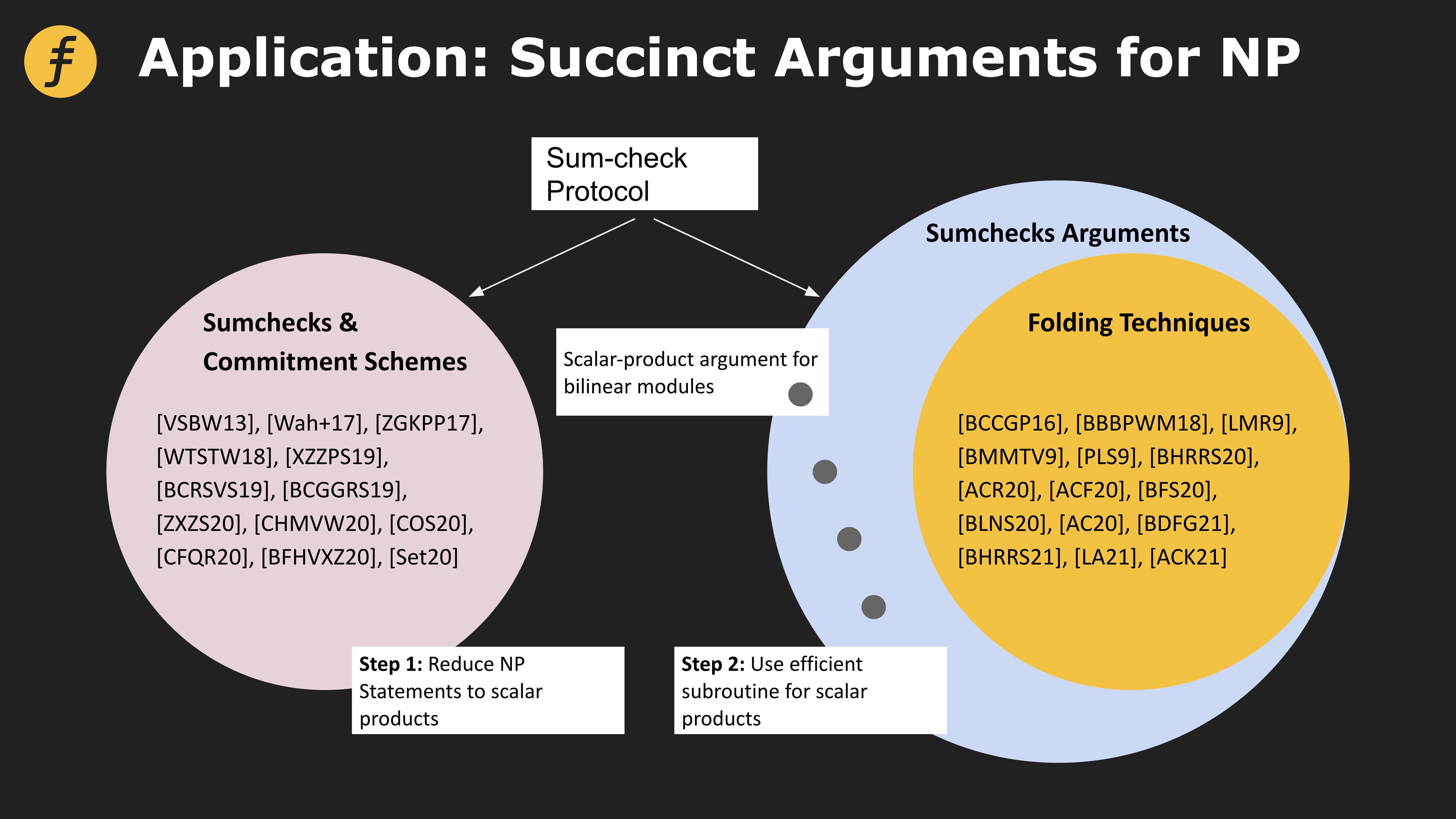
In addition, in many proof systems, the sum-check protocol is used as the underlying logic for construction. The figure below shows different proof systems based on different transformations based on sum-check.

Figure 4: Application of Sum-check protocol in four types of proof systems

first level title

epilogue

epilogue

first level title

references

1. [LFKN 92 ] Carsten Lund, Lance Fortnow, Howard Karloff, and Noam Nisan. Algebraic methods for interactive proof systems. J. ACM, 39: 859 – 868, October 1992.

2. https://people.cs.georgetown.edu/jthaler/sumcheck.pdf

3. https://zkproof.org/2020/03/16/sum-checkprotocol/

4. https://eprint.iacr.org/2021/333.pdf

5. referenceshttps://blog.csdn.net/mutourend/article/details/111610754