引言：從系統架構到可重現性保證

在傳統區塊鏈系統中，工作量證明主要依靠哈希運算的隨機性來確保安全性。而Gonka PoW 2.0面臨更複雜的挑戰：如何在基於大語言模型的計算任務中，既保證計算結果的不可預測性，又確保任何誠實節點都能重現和驗證相同的計算過程。本文將深入分析MLNode端如何透過精心設計的種子機制和確定性演算法來實現這一目標。

在深入了解特定的技術實作之前，我們需要先理解PoW 2.0系統架構的整體設計，以及可重現性在其中扮演的關鍵角色。

1. PoW 2.0系統架構概覽

1.1 分層架構設計

Gonka PoW 2.0採用分層架構，確保可重現性從區塊鏈層級貫穿到運算執行層面：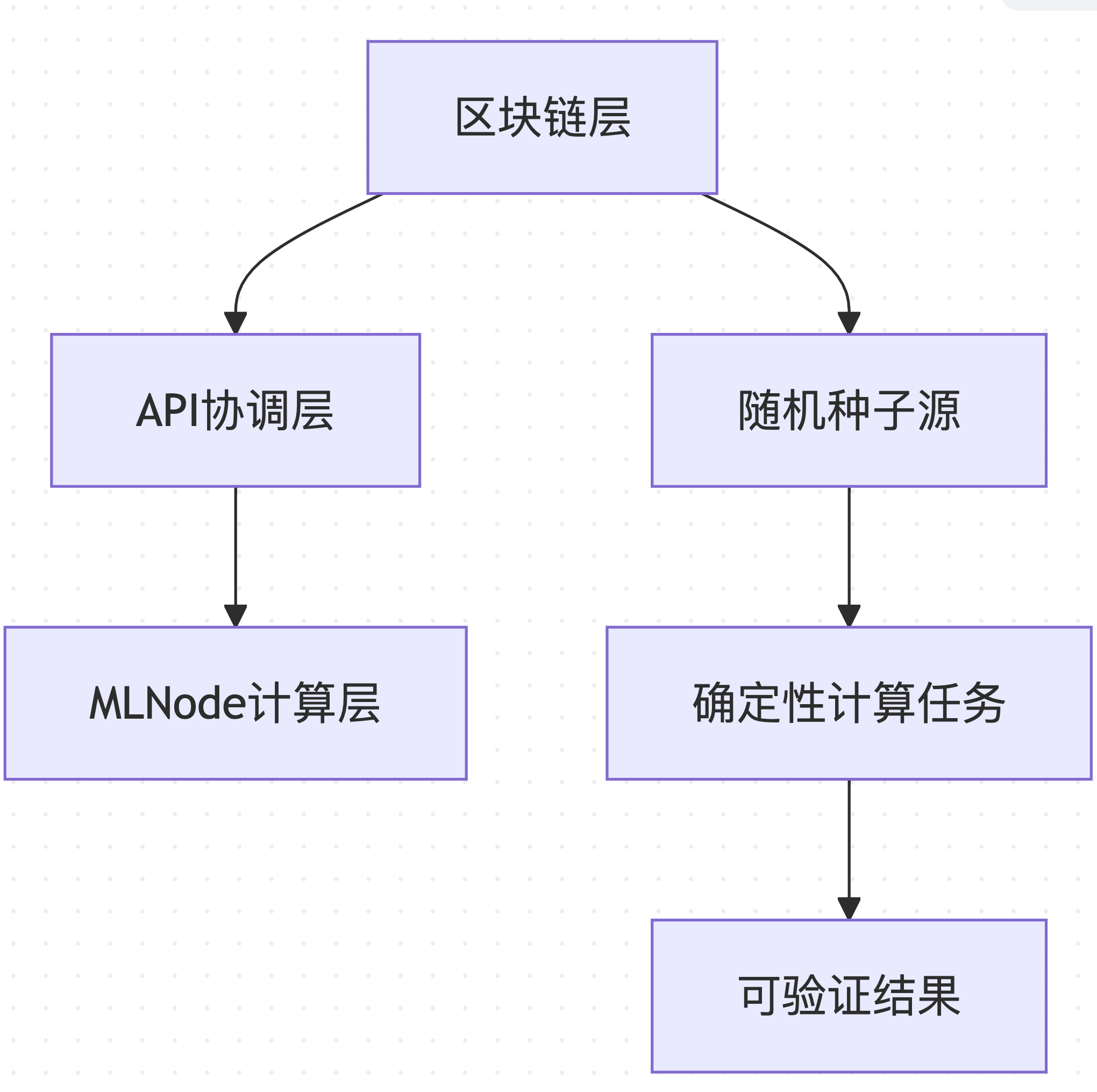

資料來源：基於decentralized-api/internal/poc 和mlnode/packages/pow 的架構設計

這種分層設計使得系統的不同元件可以獨立最佳化，同時保持整體的一致性和可驗證性。

1.2 可重現性的核心目標

PoW 2.0系統的可重現性設計服務於以下核心目標：

1.計算公平性：確保所有節點面臨相同的計算挑戰

2.結果驗證性：任何誠實節點都能重現並驗證計算結果

3.防作弊保證：使預計算和結果偽造在計算上不可行

4.網路同步：確保分散式環境下的狀態一致性

這些目標共同構成了PoW 2.0可重現性設計的基礎，確保了系統的安全性和公平性。

2. 種子系統：多層次隨機性的統一管理

在了解了系統架構之後，我們需要深入探討實現可重現性的關鍵技術—種子系統。這個系統透過多層次的隨機性管理，確保了計算的一致性和不可預測性。

2.1 種子類型與特定目標

Gonka PoW 2.0設計了四種不同類型的種子，每種種子服務於特定的計算目標：

網路級種子（Network-Level Seeds）

資料來源：decentralized-api/internal/poc/random_seed.go#L90-L111

目標：為整個網路的每個epoch提供統一的隨機性基礎，確保所有節點使用相同的全域隨機來源。

網路級種子是整個系統隨機性的根基，透過區塊鏈交易確保全網節點使用相同的隨機性基礎。

任務等級種子（Task-Level Seeds）

資料來源：mlnode/packages/pow/src/pow/random.py#L9-L21

目標：透過多輪SHA-256雜湊擴展熵空間，為每個計算任務產生高品質的隨機數產生器。

任務級種子透過擴展熵空間，為每個特定的計算任務提供高品質的隨機性。

節點級種子（Node-Level Seeds）

資料來源：種子字串建構模式`f"{hash_str}_{public_key}_nonce{nonce}"`

目標：確保不同節點和不同nonce值產生完全不同的計算路徑，防止碰撞和重複。

節點級種子透過結合節點公鑰和nonce值，確保每個節點的運算路徑都是唯一的。

目標向量種子（Target Vector Seeds）

資料來源：mlnode/packages/pow/src/pow/random.py#L165-L177

目標：為整個網路產生統一的目標向量，所有節點都朝著相同的高維度球面位置進行最佳化。

目標向量種子確保全網節點朝著相同的目標計算，這是驗證結果一致性的關鍵。

2.2 種子生命週期管理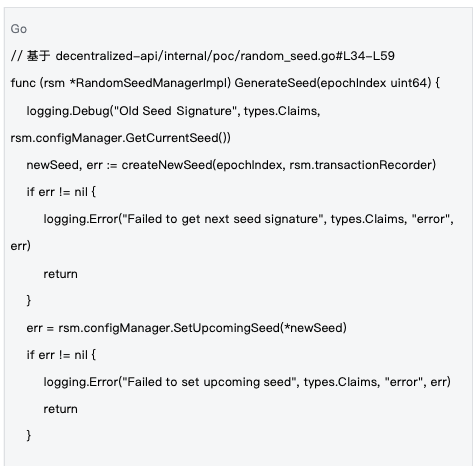

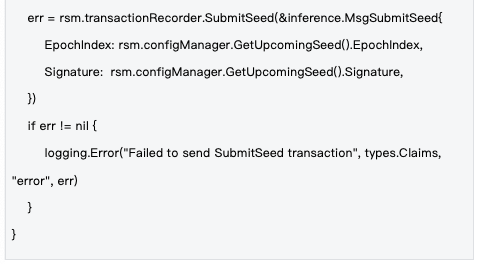
管理機制：種子在epoch層級進行管理，每個epoch開始時產生新種子，透過區塊鏈交易同步到全網，確保所有節點使用相同的隨機性基礎。

種子的生命週期管理確保了隨機性的時效性和一致性，是系統安全運作的重要保障。

3. LLM組件的種子驅動產生機制

在了解了種子系統之後，我們需要進一步探討如何將這些種子應用到LLM組件的生成過程中。這是實現可重現性的關鍵環節。

3.1 模型權重的隨機初始化

為什麼需要隨機初始化模型權重？

在傳統的深度學習中，模型權重通常透過預訓練獲得。但在PoW 2.0中，為了確保：

1.計算任務的不可預測性：相同的輸入不會因為固定權重而產生可預測的輸出

2. ASIC抗性：專用硬體無法針對固定權重進行最佳化

3.公平競爭：所有節點使用相同的隨機初始化規則

資料來源：mlnode/packages/pow/src/pow/random.py#L71-L88

隨機初始化模型權重是確保計算不可預測性和公平性的關鍵步驟。

權重初始化的確定性過程

資料來源：mlnode/packages/pow/src/pow/compute/model_init.py#L120-L125

關鍵特性：

• 使用區塊雜湊作為隨機種子，確保所有節點產生相同的權重

• 採用常態分佈N(0, 0.02²) 進行權重初始化

• 支援不同的資料型態（如float16）進行記憶體最佳化

這種確定性過程確保了不同節點在相同條件下產生完全一致的模型權重。

3.2 輸入向量生成機制

為什麼需要隨機輸入向量？

傳統PoW使用固定的資料（如交易清單）作為輸入，但PoW 2.0需要為每個nonce產生不同的輸入向量，確保：

1.搜尋空間的連續性：不同nonce對應不同的計算路徑

2.結果的不可預測性：輸入的微小變化導致輸出的巨大差異

3.驗證的高效性：驗證者可以快速重現相同的輸入

資料來源：mlnode/packages/pow/src/pow/random.py#L129-L155

隨機輸入向量的產生確保了計算的多樣性和不可預測性。

輸入生成的數學基礎

資料來源：mlnode/packages/pow/src/pow/random.py#L28-L40

技術特點：

• 每個nonce對應唯一的種子字串

• 使用標準常態分佈產生嵌入向量

• 支援批量生成以提高效率

這種數學基礎確保了輸入向量的品質和一致性。

3.3 輸出排列（Permutations）生成

為什麼需要輸出排列？

在LLM的輸出層，詞彙表通常很大（如32K-100K個token）。為了增加計算複雜度和防止針對性最佳化，系統會對輸出向量進行隨機排列：

資料來源：mlnode/packages/pow/src/pow/random.py#L158-L167

輸出排列增加了計算的複雜度，提高了系統的安全性。

排列的應用機制

資料來源：基於mlnode/packages/pow/src/pow/compute/compute.py 中的處理邏輯

設計目標：

• 增加計算挑戰的複雜度

• 防止特定詞彙表位置的最佳化

• 保持確定性以支援驗證

這種應用機制確保了排列的有效性和一致性。

4. 目標向量與球面距離計算

在了解了LLM元件的產生機制之後，我們需要進一步探討PoW 2.0中核心的運算挑戰－目標向量與球面距離計算。

4.1 什麼是目標向量？

目標向量是PoW 2.0計算挑戰的"靶心"——所有節點都嘗試讓自己的模型輸出盡可能接近這個預定的高維向量。

目標向量的數學性質

資料來源：mlnode/packages/pow/src/pow/random.py#L43-L56

關鍵特性：

• 向量位於高維單位球面上（||target|| = 1）

• 使用Marsaglia方法確保球面均勻分佈

• 所有維度具有相等的被選中機率

目標向量的數學性質確保了計算挑戰的公平性和一致性。

4.2 為什麼在球面上比較結果？

數學優勢

1.歸一化優勢：球面上的所有向量都具有單位長度，消除了向量幅度的影響

2.幾何直觀性：歐氏距離在球面上直接對應角度距離

3.數值穩定性：避免了大數值範圍所帶來的計算不穩定

高維幾何的特殊性質

在高維度空間（如4096維的詞彙表空間）中，球面分佈具有反直覺的特性：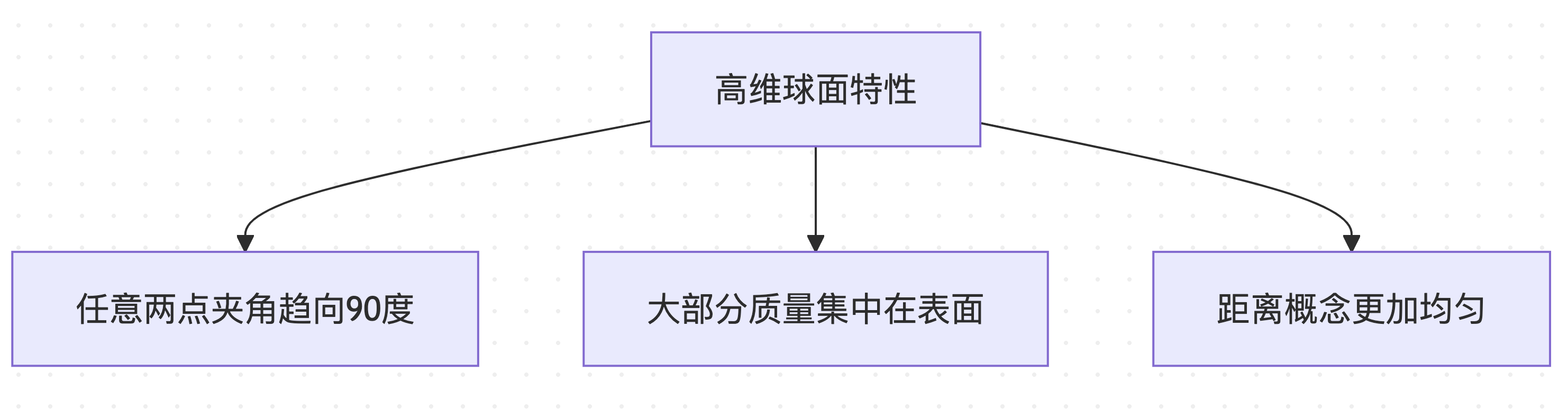

這些特殊性質使得球面距離計算成為理想的計算挑戰量測。

4.3 r_target估計與PoC階段初始化

r_target的概念與計算

r_target 是一個關鍵的難度參數，定義了"成功"計算結果的距離閾值。距離小於r_target 的結果被認為是有效的工作量證明。

資料來源：decentralized-api/mlnodeclient/poc.go#L12-L14

在Gonka PoW 2.0中，r_target 的預設值被設定為1.4013564660458173，這個值是透過大量實驗和統計分析確定的，旨在平衡計算難度和網路效率。雖然系統中有動態調整機制，但大多數情況下都會接近這個預設值。

PoC階段的r_target初始化

在每個PoC（Proof of Computation）階段開始時，系統需要：

1.評估網路算力：基於歷史資料估算目前網路的總運算能力

2.調整難度參數：設定適當的`r_target` 值以維持穩定的出塊時間

3.同步全網參數：確保所有節點使用相同的`r_target` 值

技術實現：

• r_target 值透過區塊鏈狀態同步到所有節點

• 每個PoC階段可能使用不同的r_target 值

• 自適應調整演算法根據前階段的成功率調整難度

這種初始化機制確保了網路的穩定運作和公平性。

5. 可重現性的工程保證

在了解了核心演算法之後，我們需要關注如何在工程實作上保證可重現性。這是確保系統在實際部署中穩定運作的關鍵。

5.1 確定性計算環境

資料來源：基於mlnode/packages/pow/src/pow/compute/model_init.py 的環境設置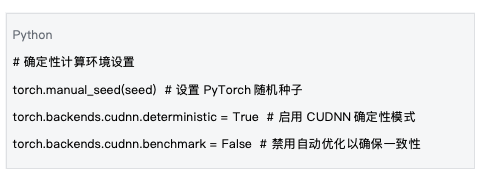

確定性計算環境的設定是保證可重現性的基礎。

5.2 數值精度管理

數值精度管理確保了在不同硬體平台上計算結果的一致性。

5.3 跨平台相容性

系統設計考慮了不同硬體平台的兼容性：

- CPU vs GPU ：支援在CPU和GPU上產生相同的運算結果

-不同GPU型號：透過標準化的數值精度確保一致性

-作業系統差異：使用標準的數學函式庫和演算法

跨平台相容性確保了系統在各種部署環境中的穩定運作。

6. 系統效能與可擴充性

在確保可重現性的基礎上，系統還需要良好的效能和可擴展性。這是確保網路高效運作的關鍵。

6.1 並行化策略

資料來源：mlnode/packages/pow/src/pow/compute/model_init.py#L26-L53

並行化策略充分利用了現代硬體的運算能力。

6.2 內存優化

系統透過多種策略優化記憶體使用：

-批次最佳化：自動調整批次大小以最大化GPU利用率

-精確度選擇：使用float16減少記憶體佔用

-梯度管理：在推理模式下停用梯度計算

記憶體優化確保了系統在資源受限環境中的高效運作。

總結：可重現性設計的工程價值

在深入分析了PoW 2.0的可重現性設計之後，我們可以總結其技術成就和工程價值。

核心技術成就

1.多層次種子管理：從網路層級到任務層級的完整種子體系，確保計算的確定性和不可預測性的平衡

2. LLM組件的系統化隨機化：模型權重、輸入向量、輸出排列的統一隨機化框架

3.高維度幾何的工程應用：利用球面幾何特性設計公平的計算挑戰

4.跨平台可重現性：透過標準化演算法和精確度控制確保不同硬體平台的一致性

這些技術成就共同構成了PoW 2.0可重現性設計的核心。

系統設計的創新價值

Gonka PoW 2.0在維持區塊鏈安全性的同時，成功地將計算資源從無意義的哈希運算轉向有價值的AI計算。其可重現性設計不僅確保了系統的公平性和安全性，也為未來的"有意義挖礦"模式提供了可行的技術範式。

技術影響：

• 為分散式AI計算提供了可驗證的執行框架

• 證明了複雜AI任務與區塊鏈共識的兼容性

• 建立了新型工作量證明的設計標準

透過精心設計的種子系統和確定性演算法，Gonka PoW 2.0實現了從傳統"浪費型安全"到"價值型安全"的根本轉變，為區塊鏈技術的可持續發展開闢了新的道路。

註：本文基於Gonka專案的實際程式碼實作編寫，所有程式碼範例和技術描述均來自專案官方程式碼庫。

關於Gonka.ai

Gonka 是一個旨在提供高效AI 算力的去中心化網絡，其設計目標是最大限度地利用全球GPU 算力，完成有意義的AI 工作負載。透過消除中心化守門人，Gonka 為開發者和研究人員提供了無需許可的算力資源訪問，同時透過其原生代幣GNK 獎勵所有參與者。

Gonka 由美國AI 開發商Product Science Inc. 孵化。該公司由Web 2 產業資深人士、前Snap Inc. 核心產品總監Libermans 兄妹創立，並於2023 年成功融資1,800 萬美元，投資者包括OpenAI 投資方Coatue Management、Solana 投資方Slow Ventures、K 5、Insight and Benchmark 合夥人等。計畫的早期貢獻者包括6 blocks、Hard Yaka、Gcore 和Bitfury 等Web 2-Web 3 領域的知名領導企業。

官網| Github | X | Discord |白皮書|經濟模型|使用手冊