บทนำ: จากสถาปัตยกรรมระบบสู่การรับรองความสามารถในการทำซ้ำ

ในระบบบล็อกเชนแบบดั้งเดิม การพิสูจน์การทำงาน (proof-of-work) อาศัยความสุ่มของการดำเนินการแฮชเป็นหลักเพื่อรับประกันความปลอดภัย อย่างไรก็ตาม Gonka PoW 2.0 เผชิญกับความท้าทายที่ซับซ้อนกว่า นั่นคือ วิธีการรับรองผลลัพธ์ที่ไม่สามารถคาดการณ์ได้สำหรับการคำนวณที่อิงจากแบบจำลองภาษาขนาดใหญ่ ขณะเดียวกันก็ต้องมั่นใจว่าโหนดที่ซื่อสัตย์ใดๆ ก็สามารถทำซ้ำและตรวจสอบกระบวนการคำนวณเดียวกันได้ บทความนี้จะเจาะลึกว่า MLNode บรรลุเป้าหมายนี้ได้อย่างไรผ่านกลไก seeding ที่ออกแบบมาอย่างพิถีพิถันและอัลกอริทึมแบบกำหนดตายตัว

ก่อนที่จะเจาะลึกถึงการใช้งานทางเทคนิคที่เฉพาะเจาะจง เราก็ต้องทำความเข้าใจการออกแบบโดยรวมของสถาปัตยกรรมระบบ PoW 2.0 และบทบาทสำคัญที่ความสามารถในการทำซ้ำได้มีอยู่ในนั้นเสียก่อน

1. ภาพรวมของสถาปัตยกรรมระบบ PoW 2.0

1.1 การออกแบบสถาปัตยกรรมแบบเลเยอร์

Gonka PoW 2.0 ใช้สถาปัตยกรรมแบบหลายชั้นเพื่อให้มั่นใจถึงความสามารถในการทำซ้ำได้ตั้งแต่ระดับบล็อคเชนไปจนถึงระดับการดำเนินการคำนวณ: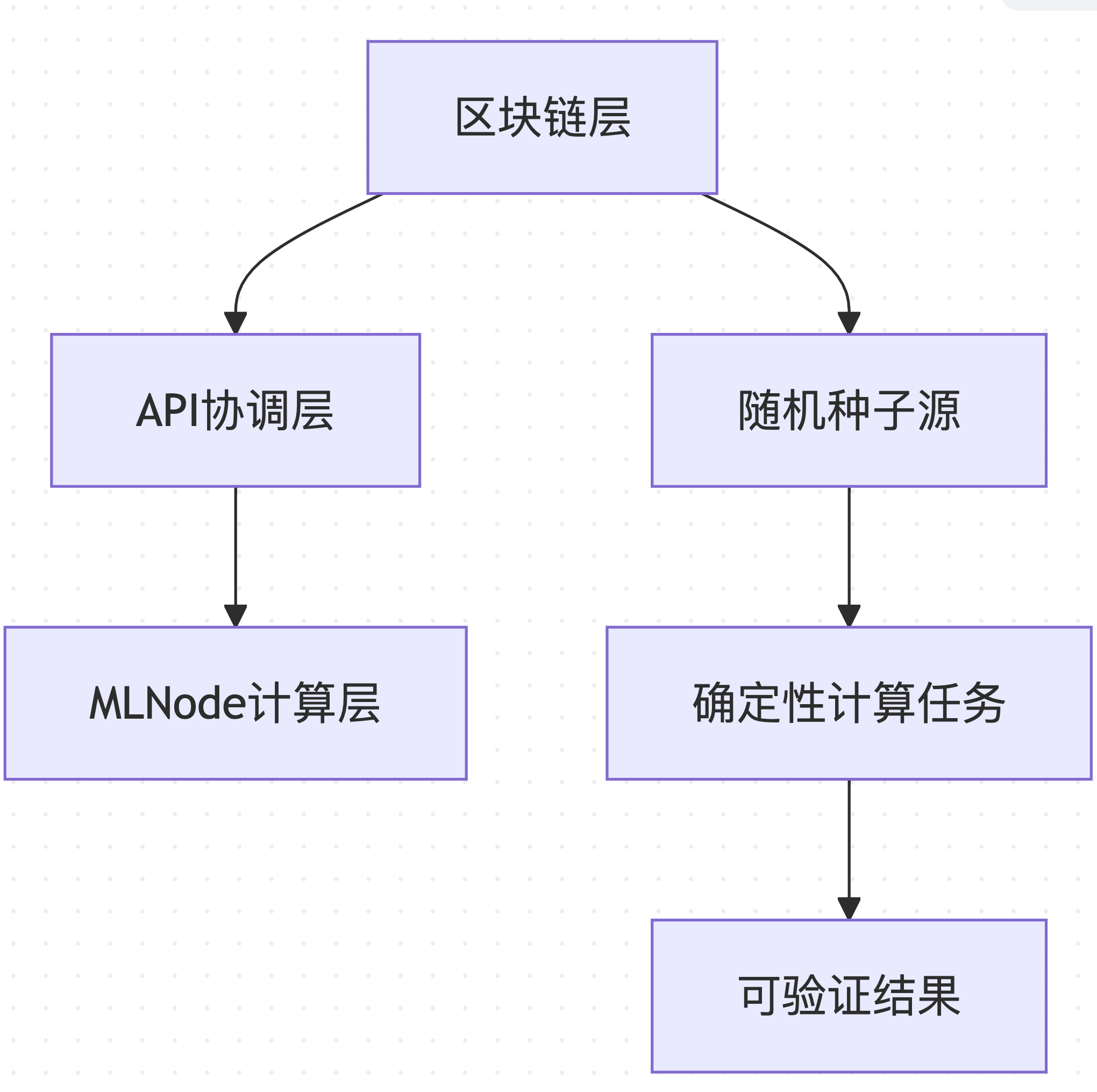

แหล่งที่มาของข้อมูล : อ้างอิงจากการออกแบบสถาปัตยกรรมของ decentralized-api/internal/poc และ mlnode/packages/pow

การออกแบบแบบหลายชั้นนี้ช่วยให้สามารถปรับส่วนประกอบต่างๆ ของระบบได้อย่างอิสระในขณะที่ยังคงความสอดคล้องและการตรวจสอบโดยรวมไว้

1.2 เป้าหมายหลักของการทำซ้ำได้

การออกแบบความสามารถในการทำซ้ำได้ของระบบ PoW 2.0 มีวัตถุประสงค์หลักดังต่อไปนี้:

1. ความยุติธรรมในการคำนวณ : การรับรองว่าโหนดทั้งหมดเผชิญกับความท้าทายในการคำนวณแบบเดียวกัน

2. การตรวจสอบผลลัพธ์ : โหนดที่ซื่อสัตย์ใดๆ ก็สามารถทำซ้ำและตรวจสอบผลลัพธ์การคำนวณได้

3. การรับประกันป้องกันการโกง : ทำให้การคำนวณล่วงหน้าและการปลอมแปลงผลลัพธ์เป็นไปไม่ได้

4. การซิงโครไนซ์เครือข่าย : การรับรองความสอดคล้องของสถานะในสภาพแวดล้อมแบบกระจาย

เป้าหมายเหล่านี้ร่วมกันก่อให้เกิดพื้นฐานของการออกแบบที่สามารถทำซ้ำได้ของ PoW 2.0 เพื่อให้แน่ใจว่าระบบมีความปลอดภัยและยุติธรรม

2. ระบบเมล็ดพันธุ์: การจัดการแบบรวมของการสุ่มหลายระดับ

หลังจากทำความเข้าใจสถาปัตยกรรมระบบแล้ว เราจำเป็นต้องเจาะลึกเทคโนโลยีสำคัญที่ช่วยให้สามารถทำซ้ำได้ นั่นคือ ระบบเมล็ดพันธุ์ (Seed System) ระบบนี้รับประกันความสม่ำเสมอและความไม่แน่นอนของการคำนวณผ่านการจัดการความสุ่มแบบหลายระดับ

2.1 ประเภทเมล็ดพันธุ์และเป้าหมายเฉพาะ

Gonka PoW 2.0 ออกแบบเมล็ดพันธุ์สี่ประเภทที่แตกต่างกัน โดยแต่ละประเภทมีเป้าหมายการคำนวณที่เฉพาะเจาะจง:

เมล็ดพันธุ์ระดับเครือข่าย

แหล่งที่มาของข้อมูล : decentralized-api/internal/poc/random_seed.go#L90-L111

เป้าหมาย : จัดทำฐานความสุ่มแบบรวมศูนย์สำหรับเครือข่ายทั้งหมดในแต่ละยุค เพื่อให้แน่ใจว่าโหนดทั้งหมดใช้แหล่งความสุ่มทั่วโลกเดียวกัน

เมล็ดพันธุ์ระดับเครือข่ายเป็นรากฐานของความสุ่มสำหรับระบบทั้งหมด โดยรับรองว่าโหนดทั้งหมดในเครือข่ายใช้รากฐานความสุ่มแบบเดียวกันผ่านธุรกรรมบล็อคเชน

เมล็ดพันธุ์ระดับงาน

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/random.py#L9-L21

เป้าหมาย : เพื่อผลิตเครื่องกำเนิดตัวเลขสุ่มคุณภาพสูงสำหรับงานคำนวณทุกงานโดยขยายพื้นที่เอนโทรปีผ่านการแฮช SHA-256 หลายรอบ

เมล็ดพันธุ์ระดับงานให้ความสุ่มคุณภาพสูงสำหรับงานคอมพิวเตอร์เฉพาะแต่ละงานโดยการขยายพื้นที่เอนโทรปี

เมล็ดพันธุ์ระดับโหนด

แหล่งที่มาของข้อมูล : รูปแบบการสร้างสตริงเมล็ดพันธุ์ `f"{hash_str}_{public_key}_nonce{nonce}"`

เป้าหมาย : ให้แน่ใจว่าโหนดที่แตกต่างกันและค่า nonce ที่แตกต่างกันสร้างเส้นทางการคำนวณที่แตกต่างกันโดยสิ้นเชิงเพื่อป้องกันการชนกันและการทำซ้ำ

เมล็ดพันธุ์ระดับโหนดช่วยให้แน่ใจว่าเส้นทางการคำนวณของแต่ละโหนดไม่ซ้ำกันโดยการรวมคีย์สาธารณะของโหนดและค่า nonce

เมล็ดพันธุ์เวกเตอร์เป้าหมาย

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/random.py#L165-L177

เป้าหมาย : สร้างเวกเตอร์เป้าหมายรวมสำหรับเครือข่ายทั้งหมด โดยที่โหนดทั้งหมดได้รับการปรับให้เหมาะสมเพื่อให้ได้ตำแหน่งทรงกลมมิติสูงเดียวกัน

เมล็ดพันธุ์เวกเตอร์เป้าหมายช่วยให้แน่ใจว่าโหนดทั้งหมดในเครือข่ายคำนวณไปสู่เป้าหมายเดียวกัน ซึ่งเป็นกุญแจสำคัญในการตรวจสอบความสอดคล้องของผลลัพธ์

2.2 การจัดการวงจรชีวิตเมล็ดพันธุ์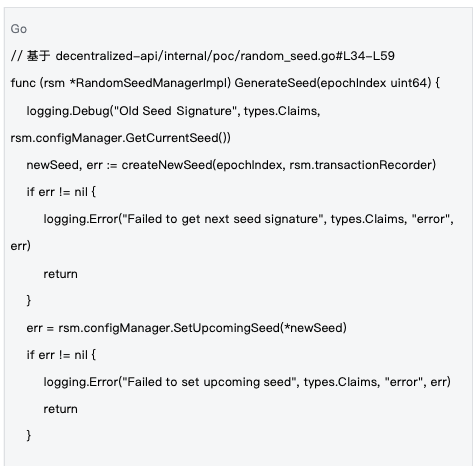

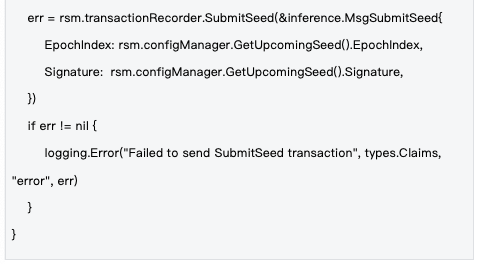
กลไกการจัดการ : เมล็ดพันธุ์ (Seeds) จะถูกจัดการที่ระดับยุค (Epoch) เมล็ดพันธุ์ใหม่จะถูกสร้างขึ้นในตอนเริ่มต้นของแต่ละยุค และซิงโครไนซ์กับเครือข่ายทั้งหมดผ่านธุรกรรมบล็อกเชน เพื่อให้มั่นใจว่าทุกโหนดจะใช้ฐานความสุ่มเดียวกัน

การจัดการวงจรชีวิตของเมล็ดพันธุ์ช่วยให้มั่นใจได้ถึงความตรงเวลาและความสม่ำเสมอของความสุ่ม และถือเป็นการรับประกันที่สำคัญสำหรับการดำเนินงานที่ปลอดภัยของระบบ

3. กลไกการสร้างเมล็ดพันธุ์ที่ขับเคลื่อนด้วยส่วนประกอบ LLM

ตอนนี้เรามีความเข้าใจที่ชัดเจนเกี่ยวกับระบบเมล็ดพันธุ์แล้ว เราจำเป็นต้องศึกษาวิธีการนำเมล็ดพันธุ์เหล่านี้ไปใช้กับการสร้างส่วนประกอบ LLM นี่คือกุญแจสำคัญในการบรรลุความสามารถในการทำซ้ำได้

3.1 การเริ่มต้นแบบสุ่มของน้ำหนักแบบจำลอง

เหตุใดเราจึงต้องกำหนดค่าเริ่มต้นน้ำหนักโมเดลแบบสุ่ม?

ในการเรียนรู้เชิงลึกแบบดั้งเดิม มักจะได้น้ำหนักของโมเดลผ่านการฝึกอบรมเบื้องต้น อย่างไรก็ตาม ใน PoW 2.0 เพื่อให้แน่ใจว่า:

1. ความไม่แน่นอนของงานการคำนวณ : อินพุตเดียวกันจะไม่สร้างเอาต์พุตที่คาดเดาได้เนื่องจากน้ำหนักคงที่

2. ความต้านทาน ASIC : ฮาร์ดแวร์เฉพาะทางไม่สามารถปรับให้เหมาะสมกับน้ำหนักคงที่ได้

3. การแข่งขันที่เป็นธรรม : โหนดทั้งหมดใช้กฎการเริ่มต้นแบบสุ่มแบบเดียวกัน

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/random.py#L71-L88

การกำหนดค่าเริ่มต้นน้ำหนักของโมเดลแบบสุ่มเป็นขั้นตอนสำคัญเพื่อให้แน่ใจว่าการคำนวณมีความไม่แน่นอนและมีความยุติธรรม

กระบวนการกำหนดสำหรับการเริ่มต้นน้ำหนัก

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/compute/model_init.py#L120-L125

คุณสมบัติหลัก :

• ใช้แฮชบล็อกเป็นเมล็ดพันธุ์สุ่มเพื่อให้แน่ใจว่าโหนดทั้งหมดสร้างน้ำหนักเท่ากัน

• ใช้การแจกแจงแบบปกติ N(0, 0.02²) สำหรับการเริ่มต้นน้ำหนัก

• รองรับประเภทข้อมูลที่แตกต่างกัน (เช่น float16) สำหรับการเพิ่มประสิทธิภาพหน่วยความจำ

กระบวนการกำหนดนี้รับประกันว่าโหนดต่างๆ จะสร้างน้ำหนักโมเดลที่เหมือนกันทุกประการภายใต้เงื่อนไขเดียวกัน

3.2 กลไกการสร้างเวกเตอร์อินพุต

เหตุใดเราจึงต้องใช้เวกเตอร์อินพุตแบบสุ่ม?

PoW แบบดั้งเดิมใช้ข้อมูลคงที่ (เช่น รายการธุรกรรม) เป็นอินพุต แต่ PoW 2.0 จำเป็นต้องสร้างเวกเตอร์อินพุตที่แตกต่างกันสำหรับแต่ละ nonce เพื่อให้แน่ใจว่า:

1. ความต่อเนื่องของพื้นที่การค้นหา : nonce ที่แตกต่างกันสอดคล้องกับเส้นทางการคำนวณที่แตกต่างกัน

2. ผลลัพธ์ที่ไม่สามารถคาดเดาได้ : การเปลี่ยนแปลงเล็กน้อยในอินพุตนำไปสู่ความแตกต่างที่มากในเอาต์พุต

3. ประสิทธิภาพของการตรวจสอบ : ผู้ตรวจสอบสามารถทำซ้ำข้อมูลอินพุตเดียวกันได้อย่างรวดเร็ว

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/random.py#L129-L155

การสร้างเวกเตอร์อินพุตแบบสุ่มช่วยให้การคำนวณมีความหลากหลายและไม่สามารถคาดเดาได้

พื้นฐานทางคณิตศาสตร์สำหรับการสร้างอินพุต

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/random.py#L28-L40

คุณสมบัติทางเทคนิค :

• nonce แต่ละอันจะสอดคล้องกับสตริงเมล็ดพันธุ์เฉพาะ

• สร้างเวกเตอร์ฝังตัวโดยใช้การแจกแจงแบบปกติมาตรฐาน

• รองรับการสร้างชุดเพื่อปรับปรุงประสิทธิภาพ

รากฐานทางคณิตศาสตร์นี้รับประกันคุณภาพและความสอดคล้องของเวกเตอร์อินพุต

3.3 การสร้างการเรียงสับเปลี่ยนผลลัพธ์

เพราะเหตุใดเราจึงต้องแสดงผลการเรียงสับเปลี่ยน?

ในเลเยอร์เอาต์พุตของ LLM คำศัพท์มักจะมีขนาดใหญ่ (เช่น โทเค็น 32,000-100,000 โทเค็น) เพื่อเพิ่มความซับซ้อนในการคำนวณและป้องกันการเพิ่มประสิทธิภาพแบบเจาะจง ระบบจะสุ่มสับเปลี่ยนเวกเตอร์เอาต์พุต:

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/random.py#L158-L167

การสับเปลี่ยนผลลัพธ์จะเพิ่มความซับซ้อนของการคำนวณและปรับปรุงความปลอดภัยของระบบ

กลไกการใช้งานการจัดเตรียม

แหล่งที่มาของข้อมูล : อ้างอิงจากตรรกะการประมวลผลใน mlnode/packages/pow/src/pow/compute/compute.py

เป้าหมายการออกแบบ :

• เพิ่มความซับซ้อนของความท้าทายในการคำนวณ

• ป้องกันการปรับปรุงตำแหน่งคำศัพท์เฉพาะ

• การรักษาความแน่นอนเพื่อสนับสนุนการตรวจสอบ

กลไกการใช้งานนี้ช่วยให้มั่นใจถึงความถูกต้องและความสอดคล้องของการจัดเตรียม

4. การคำนวณระยะทางระหว่างเวกเตอร์เป้าหมายและทรงกลม

หลังจากทำความเข้าใจกลไกการสร้างส่วนประกอบ LLM แล้ว เราจำเป็นต้องสำรวจความท้าทายในการคำนวณหลักใน PoW 2.0 เพิ่มเติม ซึ่งก็คือการคำนวณระยะห่างระหว่างเวกเตอร์เป้าหมายและทรงกลม

4.1 เวกเตอร์เป้าหมายคืออะไร?

เวกเตอร์เป้าหมายคือ "จุดสนใจ" ของความท้าทายในการคำนวณของ PoW 2.0 โหนดทั้งหมดพยายามทำให้เอาต์พุตของโมเดลใกล้เคียงกับเวกเตอร์มิติสูงที่กำหนดไว้ล่วงหน้าให้มากที่สุด

คุณสมบัติทางคณิตศาสตร์ของเวกเตอร์เป้าหมาย

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/random.py#L43-L56

คุณสมบัติหลัก :

• เวกเตอร์วางอยู่บนทรงกลมหน่วยมิติสูง (||เป้าหมาย|| = 1)

• ใช้หลักการของ Marsaglia เพื่อให้แน่ใจว่ามีการกระจายสม่ำเสมอทั่วทรงกลม

• มิติทั้งหมดมีความน่าจะเป็นที่จะถูกเลือกเท่ากัน

คุณสมบัติทางคณิตศาสตร์ของเวกเตอร์เป้าหมายช่วยให้มั่นใจถึงความยุติธรรมและความสอดคล้องในความท้าทายในการคำนวณ

4.2 เหตุใดจึงต้องเปรียบเทียบผลลัพธ์บนทรงกลม?

ข้อได้เปรียบทางคณิตศาสตร์

1. ข้อดีของการทำให้เป็นมาตรฐาน : เวกเตอร์ทั้งหมดบนทรงกลมมีความยาวหน่วย ซึ่งขจัดอิทธิพลของขนาดเวกเตอร์

2. สัญชาตญาณทางเรขาคณิต : ระยะทางแบบยุคลิดบนทรงกลมจะสัมพันธ์โดยตรงกับระยะทางเชิงมุม

3. เสถียรภาพเชิงตัวเลข : หลีกเลี่ยงความไม่เสถียรในการคำนวณที่เกิดจากช่วงตัวเลขขนาดใหญ่

คุณสมบัติพิเศษของรูปทรงเรขาคณิตมิติสูง

ในพื้นที่มิติสูง (เช่น พื้นที่คำศัพท์ 4096 มิติ) การกระจายทรงกลมมีคุณสมบัติที่ขัดกับสัญชาตญาณ: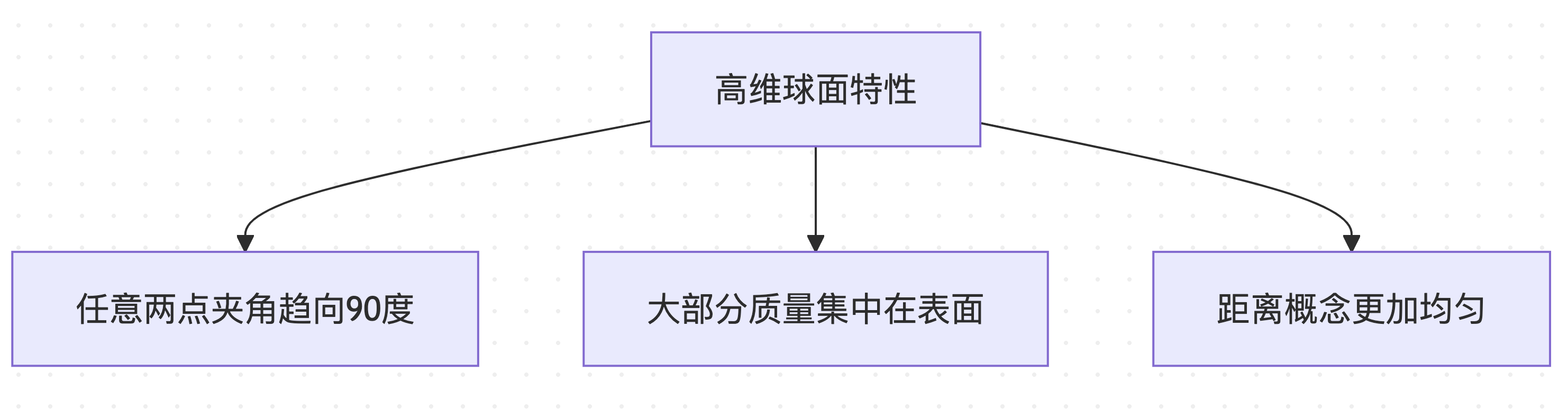

คุณสมบัติพิเศษเหล่านี้ทำให้การคำนวณระยะทางทรงกลมเป็นหน่วยวัดที่ท้าทายทางการคำนวณที่เหมาะสม

4.3 การประมาณค่า r_target และการเริ่มต้นขั้นตอน PoC

แนวคิดและการคำนวณของ r_target

r_target เป็นพารามิเตอร์ความยากหลักที่กำหนดเกณฑ์ระยะทางสำหรับผลลัพธ์การคำนวณที่ "สำเร็จ" ผลลัพธ์ที่มีระยะทางน้อยกว่า r_target ถือเป็นหลักฐานการทำงานที่ถูกต้อง

แหล่งที่มาของข้อมูล : decentralized-api/mlnodeclient/poc.go#L12-L14

ใน Gonka PoW 2.0 ค่าเริ่มต้นของ r_target ถูกตั้งไว้ที่ 1.4013564660458173 ค่านี้ถูกกำหนดโดยการทดลองและการวิเคราะห์ทางสถิติอย่างละเอียด เพื่อสร้างสมดุลระหว่างความยากในการคำนวณและประสิทธิภาพของเครือข่าย แม้ว่าจะมีกลไกการปรับแบบไดนามิกในระบบ แต่ในกรณีส่วนใหญ่ก็จะใกล้เคียงกับค่าเริ่มต้นนี้

การเริ่มต้น r_target ในระยะ PoC

ในช่วงเริ่มต้นของแต่ละเฟส PoC (Proof of Computation) ระบบจะต้อง:

1. ประเมินพลังการประมวลผลเครือข่าย : ประเมินพลังการประมวลผลทั้งหมดของเครือข่ายปัจจุบันโดยอิงจากข้อมูลในอดีต

2. ปรับพารามิเตอร์ความยาก : ตั้งค่า `r_target` ที่เหมาะสมเพื่อรักษาเวลาบล็อกให้คงที่

3. ซิงโครไนซ์พารามิเตอร์ทั่วทั้งเครือข่าย : ตรวจสอบให้แน่ใจว่าโหนดทั้งหมดใช้ค่า `r_target` เดียวกัน

การดำเนินการทางเทคนิค :

• ค่า r_target จะถูกซิงโครไนซ์กับโหนดทั้งหมดผ่านสถานะบล็อคเชน

• แต่ละขั้นตอน PoC อาจใช้ค่า r_target ที่แตกต่างกัน

• อัลกอริธึมการปรับแบบปรับตัวจะปรับระดับความยากตามอัตราความสำเร็จของด่านก่อนหน้า

กลไกการเริ่มต้นนี้ช่วยให้มั่นใจถึงการทำงานที่เสถียรและความยุติธรรมของเครือข่าย

5. การรับรองทางวิศวกรรมของความสามารถในการทำซ้ำได้

หลังจากเข้าใจอัลกอริทึมหลักแล้ว เราต้องมุ่งเน้นไปที่วิธีการรับประกันความสามารถในการทำซ้ำได้ในการใช้งานทางวิศวกรรม นี่คือกุญแจสำคัญในการรับประกันการทำงานที่เสถียรของระบบในการใช้งานจริง

5.1 สภาพแวดล้อมการคำนวณแบบกำหนดแน่นอน

แหล่งที่มาของข้อมูล : อิงตามการตั้งค่าสภาพแวดล้อมของ mlnode/packages/pow/src/pow/compute/model_init.py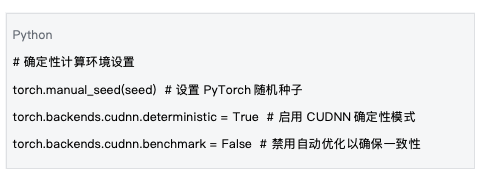

การจัดตั้งสภาพแวดล้อมการคำนวณแบบกำหนดได้เป็นพื้นฐานในการรับรองความสามารถในการทำซ้ำได้

5.2 การจัดการความแม่นยำเชิงตัวเลข

การจัดการความแม่นยำเชิงตัวเลขช่วยให้มั่นใจถึงความสอดคล้องของผลการคำนวณบนแพลตฟอร์มฮาร์ดแวร์ที่แตกต่างกัน

5.3 ความเข้ากันได้ข้ามแพลตฟอร์ม

การออกแบบระบบคำนึงถึงความเข้ากันได้ของแพลตฟอร์มฮาร์ดแวร์ที่แตกต่างกัน:

- CPU เทียบกับ GPU : รองรับการสร้างผลลัพธ์การคำนวณแบบเดียวกันทั้งบน CPU และ GPU

-โมเดล GPU ที่แตกต่างกัน : รับรองความสม่ำเสมอผ่านความแม่นยำเชิงตัวเลขมาตรฐาน

- ความแตกต่างของระบบปฏิบัติการ : ใช้ไลบรารีและอัลกอริทึมทางคณิตศาสตร์มาตรฐาน

ความเข้ากันได้ข้ามแพลตฟอร์มช่วยให้ระบบทำงานได้อย่างเสถียรในสภาพแวดล้อมการใช้งานต่างๆ

6. ประสิทธิภาพและความสามารถในการปรับขนาดของระบบ

เพื่อให้แน่ใจว่าสามารถทำซ้ำได้ ระบบยังต้องมีประสิทธิภาพที่ดีและมีความสามารถในการปรับขนาดได้ ซึ่งถือเป็นกุญแจสำคัญในการรับรองการทำงานที่มีประสิทธิภาพของเครือข่าย

6.1 กลยุทธ์การทำงานแบบคู่ขนาน

แหล่งที่มาของข้อมูล : mlnode/packages/pow/src/pow/compute/model_init.py#L26-L53

กลยุทธ์การประมวลผลแบบคู่ขนานใช้ประโยชน์จากพลังการประมวลผลของฮาร์ดแวร์สมัยใหม่ได้อย่างเต็มที่

6.2 การเพิ่มประสิทธิภาพหน่วยความจำ

ระบบจะเพิ่มประสิทธิภาพการใช้หน่วยความจำโดยใช้กลยุทธ์ต่างๆ:

- การเพิ่มประสิทธิภาพแบบแบตช์ : ปรับขนาดแบตช์โดยอัตโนมัติเพื่อเพิ่มการใช้ GPU ให้สูงสุด

-การเลือกความแม่นยำ : ใช้ float16 เพื่อลดการใช้หน่วยความจำ

- การจัดการการไล่ระดับสี : ปิดใช้งานการคำนวณการไล่ระดับสีในโหมดอนุมาน

การเพิ่มประสิทธิภาพหน่วยความจำช่วยให้ระบบทำงานได้อย่างมีประสิทธิภาพในสภาพแวดล้อมที่มีทรัพยากรจำกัด

สรุป: คุณค่าทางวิศวกรรมของการออกแบบที่ทำซ้ำได้

หลังจากวิเคราะห์เชิงลึกเกี่ยวกับการออกแบบที่ทำซ้ำได้ของ PoW 2.0 แล้ว เราสามารถสรุปความสำเร็จทางเทคนิคและคุณค่าทางวิศวกรรมได้

ความสำเร็จด้านเทคโนโลยีหลัก

1. การจัดการเมล็ดพันธุ์หลายระดับ : ระบบเมล็ดพันธุ์ที่สมบูรณ์ตั้งแต่ระดับเครือข่ายไปจนถึงระดับงานเพื่อให้แน่ใจว่ามีความสมดุลระหว่างการกำหนดล่วงหน้าและความไม่แน่นอนในการประมวลผล

2. การสุ่มแบบเป็นระบบของส่วนประกอบ LLM : กรอบการสุ่มแบบรวมสำหรับน้ำหนักแบบจำลอง เวกเตอร์อินพุต และการเรียงสับเปลี่ยนเอาต์พุต

3. การประยุกต์ใช้ทางวิศวกรรมของเรขาคณิตมิติสูง : การออกแบบความท้าทายในการคำนวณอย่างยุติธรรมโดยใช้คุณสมบัติทางเรขาคณิตทรงกลม

4. การทำซ้ำข้ามแพลตฟอร์ม : รับรองความสม่ำเสมอข้ามแพลตฟอร์มฮาร์ดแวร์ต่างๆ ผ่านอัลกอริทึมมาตรฐานและการควบคุมที่แม่นยำ

ความสำเร็จทางเทคนิคเหล่านี้ร่วมกันก่อให้เกิดแกนหลักของการออกแบบที่สามารถทำซ้ำได้ของ PoW 2.0

คุณค่าเชิงนวัตกรรมของการออกแบบระบบ

ขณะเดียวกันก็รักษาความปลอดภัยของบล็อกเชน Gonka PoW 2.0 ประสบความสำเร็จในการเปลี่ยนทรัพยากรการประมวลผลจากการดำเนินการแฮชที่ไม่มีความหมายไปสู่การประมวลผล AI ที่มีคุณค่า การออกแบบที่สามารถทำซ้ำได้นี้ไม่เพียงแต่รับประกันความยุติธรรมและความปลอดภัยของระบบเท่านั้น แต่ยังมอบกระบวนทัศน์ทางเทคนิคที่ใช้งานได้จริงสำหรับโมเดล "การขุดแบบมีนัยสำคัญ" ในอนาคตอีกด้วย

ผลกระทบทางเทคนิค :

• มอบกรอบการทำงานที่ตรวจสอบได้สำหรับการประมวลผล AI แบบกระจาย

• แสดงให้เห็นถึงความเข้ากันได้ของงาน AI ที่ซับซ้อนกับฉันทามติบล็อคเชน

• กำหนดมาตรฐานการออกแบบสำหรับการพิสูจน์การทำงานประเภทใหม่

ด้วยระบบเมล็ดพันธุ์ที่ได้รับการออกแบบอย่างรอบคอบและอัลกอริทึมที่กำหนดไว้ล่วงหน้า Gonka PoW 2.0 ประสบความสำเร็จในการเปลี่ยนแปลงครั้งสำคัญจาก "ความปลอดภัยตามขยะ" แบบดั้งเดิมไปเป็น "ความปลอดภัยตามมูลค่า" โดยเปิดเส้นทางใหม่สำหรับการพัฒนาเทคโนโลยีบล็อคเชนอย่างยั่งยืน

หมายเหตุ: บทความนี้อ้างอิงจากการใช้งานโค้ดจริงของโครงการ Gonka ตัวอย่างโค้ดและคำอธิบายทางเทคนิคทั้งหมดมาจากคลังโค้ดอย่างเป็นทางการของโครงการ

เกี่ยวกับ Gonka.ai

Gonka คือเครือข่ายแบบกระจายศูนย์ที่ออกแบบมาเพื่อมอบพลังการประมวลผล AI ที่มีประสิทธิภาพ เป้าหมายการออกแบบคือการเพิ่มประสิทธิภาพการใช้พลังการประมวลผล GPU ทั่วโลกให้สูงสุดเพื่อจัดการเวิร์กโหลด AI ที่สำคัญ ด้วยการขจัดระบบเกตเวย์แบบรวมศูนย์ Gonka จึงช่วยให้นักพัฒนาและนักวิจัยเข้าถึงทรัพยากรการประมวลผลได้โดยไม่ต้องขออนุญาต ขณะเดียวกันก็มอบโทเค็น GNK ดั้งเดิมให้กับผู้เข้าร่วมทุกคน

Gonka ได้รับการบ่มเพาะโดย Product Science Inc. ผู้พัฒนา AI สัญชาติอเมริกัน ก่อตั้งโดยพี่น้องตระกูล Liberman ผู้คร่ำหวอดในวงการ Web 2 และอดีตผู้อำนวยการฝ่ายผลิตภัณฑ์หลักของ Snap Inc. บริษัทประสบความสำเร็จในการระดมทุน 18 ล้านดอลลาร์ในปี 2023 จากนักลงทุน ได้แก่ Coatue Management ซึ่งเป็นนักลงทุนใน OpenAI, Slow Ventures ซึ่งเป็นนักลงทุนใน Solana, K5, Insight และ Benchmark Partners ผู้ร่วมก่อตั้งโครงการในช่วงแรก ๆ ได้แก่ ผู้นำที่มีชื่อเสียงในวงการ Web 2-Web 3 เช่น 6 Blocks, Hard Yaka, Gcore และ Bitfury

เว็บไซต์อย่างเป็นทางการ | Github | X | Discord | เอกสารเผยแพร่ | แบบจำลองเศรษฐกิจ | คู่มือผู้ใช้