LUCIDA:如何利用多因子策略构建强大的加密资产投资组合(因子合成篇)
ต่อจากบทที่แล้ว เราได้เผยแพร่บทความสามบทความในชุดบทความเกี่ยวกับ การสร้างพอร์ตโฟลิโอสินทรัพย์ดิจิทัลที่มีประสิทธิภาพโดยใช้แบบจำลองหลายปัจจัย:“พื้นฐานทางทฤษฎี”、“การประมวลผลข้อมูลล่วงหน้า”、การทดสอบความถูกต้องของปัจจัย。
บทความสามบทความแรกอธิบายทฤษฎีของกลยุทธ์หลายปัจจัยและขั้นตอนของการทดสอบปัจจัยเดียวตามลำดับ
1. เหตุผลในการทดสอบความสัมพันธ์ของปัจจัย: ความหลากหลาย
เราคัดกรองปัจจัยที่มีประสิทธิผลชุดหนึ่งผ่านการทดสอบปัจจัยเดียว แต่ปัจจัยข้างต้นไม่สามารถป้อนลงในฐานข้อมูลได้โดยตรง ปัจจัยต่างๆ เองสามารถแบ่งออกได้เป็นหมวดหมู่กว้างๆ ตามความหมายทางเศรษฐกิจเฉพาะ ปัจจัยประเภทเดียวกันมีความสัมพันธ์กันอย่างมาก หากนำมาลงในฐานข้อมูลโดยตรงโดยไม่มีการคัดกรองความสัมพันธ์ และดำเนินการถดถอยเชิงเส้นพหุคูณเพื่อคำนวณอัตราผลตอบแทนที่คาดหวัง ขึ้นอยู่กับปัจจัยที่แตกต่างกัน จะเกิดปัญหา Multicollinearity ในเศรษฐมิติ ความเป็นหลายคอลลิเนียร์หมายความว่าตัวแปรอธิบายบางส่วนหรือทั้งหมดในแบบจำลองการถดถอยมีความสัมพันธ์เชิงเส้นตรง สมบูรณ์ หรือแม่นยำ (ความสัมพันธ์สูงระหว่างตัวแปร)
ดังนั้น หลังจากกรองปัจจัยที่มีประสิทธิผลออกแล้ว จึงจำเป็นต้องทำการทดสอบ T กับความสัมพันธ์ของปัจจัยตามหมวดหมู่หลักๆ ก่อน สำหรับปัจจัยที่มีความสัมพันธ์กันสูงกว่า ให้ละทิ้งปัจจัยที่มีนัยสำคัญต่ำกว่าหรือทำการสังเคราะห์ปัจจัย
คำอธิบายทางคณิตศาสตร์ของพหุคอลลิเนียริตี้มีดังนี้:
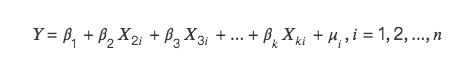
จะมีสองสถานการณ์:

ผลที่ตามมาของความหลากหลาย:
1. ไม่มีตัวประมาณค่าพารามิเตอร์ภายใต้ความเป็นเส้นตรงที่สมบูรณ์แบบ
2. ตัวประมาณค่า OLS ไม่ถูกต้องภายใต้ความใกล้เคียงกันโดยประมาณ


3. ความสำคัญทางเศรษฐกิจของตัวประมาณค่าพารามิเตอร์นั้นไม่สมเหตุสมผล
4. การทดสอบนัยสำคัญของตัวแปร (t test) สูญเสียนัยสำคัญ
5. ฟังก์ชันการทำนายของแบบจำลองล้มเหลว: อัตราผลตอบแทนที่คาดการณ์ไว้ซึ่งติดตั้งโดยแบบจำลองเชิงเส้นหลายตัวแปรนั้นไม่ถูกต้องอย่างยิ่ง และแบบจำลองล้มเหลว
2. ขั้นตอนที่ 1: การทดสอบความสัมพันธ์ของปัจจัยประเภทเดียวกัน
ทดสอบความสัมพันธ์ระหว่างปัจจัยที่คำนวณใหม่กับปัจจัยที่มีอยู่ในฐานข้อมูลแล้ว โดยทั่วไปแล้ว มีข้อมูลสองประเภทสำหรับความสัมพันธ์:
1. คำนวณความสัมพันธ์ตามค่าตัวประกอบของโทเค็นทั้งหมดในช่วง backtest
2. คำนวณความสัมพันธ์โดยพิจารณาจากค่าส่งคืนส่วนเกินของโทเค็นทั้งหมดในช่วง backtest

แต่ละปัจจัยที่เราแสวงหามีส่วนสนับสนุนและอำนาจในการอธิบายอัตราการส่งคืนของโทเค็น วัตถุประสงค์ของการดำเนินการทดสอบความสัมพันธ์** คือการค้นหาปัจจัยที่มีคำอธิบายและส่วนสนับสนุนที่แตกต่างกันต่อผลตอบแทนของกลยุทธ์ เป้าหมายสูงสุดของกลยุทธ์คือผลตอบแทน** หากปัจจัยทั้งสองอธิบายผลตอบแทนที่เหมือนกัน จะไม่มีความหมายแม้ว่าค่าปัจจัยทั้งสองจะแตกต่างกันอย่างมีนัยสำคัญก็ตาม ดังนั้นเราจึงไม่ต้องการค้นหาปัจจัยที่มีค่าตัวประกอบต่างกันมาก แต่ต้องการค้นหาปัจจัยที่มีปัจจัยต่างกันที่อธิบายผลตอบแทน ดังนั้นในที่สุดเราจึงเลือกใช้ค่าส่งคืนส่วนเกินของตัวประกอบในการคำนวณความสัมพันธ์
กลยุทธ์ของเราคือความถี่รายวัน ดังนั้นเราจึงคำนวณเมทริกซ์สัมประสิทธิ์สหสัมพันธ์ระหว่างปัจจัยที่ส่งคืนส่วนเกินตามวันที่ของช่วงการทดสอบย้อนกลับ

แก้ทางโปรแกรมเพื่อหาปัจจัย n อันดับแรกที่มีความสัมพันธ์สูงสุดในไลบรารี:
def get_n_max_corr(self, factors, n= 1):
factors_excess = self.get_excess_returns(factors)
save_factor_excess = self.get_excess_return(self.factor_value, self.start_date, self.end_date)
if len(factors_excess) < 1:
return factor_excess, 1.0, None
factors_excess[self.factor_name] = factor_excess['excess_return']
factors_excess = pd.concat(factors_excess, axis= 1)
factors_excess.columns = factors_excess.columns.levels[ 0 ]
# get corr matrix
factor_corr = factors_excess.corr()
factor_corr_df = factor_corr.abs().loc[self.factor_name]
max_corr_score = factor_corr_df.sort_values(ascending=False).iloc[ 1:].head(n)
return save_factor_excess, factor_corr_df, max_corr_score
3. ขั้นตอนที่ 2: การเลือกปัจจัยและการสังเคราะห์ปัจจัย
สำหรับชุดปัจจัยที่มีความสัมพันธ์สูง มีสองวิธีในการจัดการกับปัจจัยเหล่านี้:
(1) การเลือกปัจจัย
ขึ้นอยู่กับค่า ICIR อัตราผลตอบแทน อัตราการหมุนเวียน และอัตราส่วน Sharpe ของปัจจัยนั้นเอง ปัจจัยที่มีประสิทธิผลมากที่สุดในมิติหนึ่งๆ จะถูกเลือกเพื่อคงไว้ และปัจจัยอื่นๆ จะถูกลบออก
(2) การสังเคราะห์ปัจจัย
สังเคราะห์ปัจจัยในชุดปัจจัยและเก็บข้อมูลที่มีประสิทธิภาพมากที่สุดเท่าที่จะเป็นไปได้ในหน้าตัดขวาง

สมมติว่าปัจจุบันมีเมทริกซ์ปัจจัย 3 ตัวที่ต้องประมวลผล:

2.1 การถ่วงน้ำหนักที่เท่ากัน
น้ำหนักของแต่ละปัจจัยจะเท่ากัน (w= 1/จำนวนปัจจัย) และปัจจัยที่ครอบคลุม = ผลรวมของค่าของแต่ละปัจจัยเป็นค่าเฉลี่ย
เช่น ปัจจัยโมเมนตัม อัตราผลตอบแทน 1 เดือน อัตราผลตอบแทน 2 เดือน อัตราผลตอบแทน 3 เดือน อัตราผลตอบแทน 6 เดือน อัตราผลตอบแทน 12 เดือน ปัจจัยโหลดของปัจจัยทั้ง 6 ประการที่แต่ละปัจจัยพิจารณา 1/6 ของน้ำหนัก สังเคราะห์การโหลดปัจจัยโมเมนตัมใหม่ จากนั้นดำเนินการทำให้เป็นมาตรฐานอีกครั้ง
การสังเคราะห์ 1 = synthetic.mean(axis= 1) # หาค่าเฉลี่ยทีละแถว
2.2 การถ่วงน้ำหนัก IC ในอดีต, ICIR ในอดีต, การถ่วงน้ำหนักรายได้ในอดีต
ปัจจัยต่างๆ ได้รับการถ่วงน้ำหนักด้วยค่า IC (ค่า ICIR, ค่าที่ส่งคืนในอดีต) ในช่วงเวลาการทดสอบย้อนหลัง มีหลายช่วงในอดีต และแต่ละช่วงมีค่า IC ดังนั้นจึงใช้ค่าเฉลี่ยเป็นน้ำหนักของตัวประกอบ เป็นเรื่องปกติที่จะใช้ค่าเฉลี่ย (ค่าเฉลี่ยเลขคณิต) ของ IC ในช่วง backtest เป็นน้ำหนัก

2.3 การถ่วงน้ำหนักครึ่งชีวิต ICIR ในอดีต, การถ่วงน้ำหนักครึ่งชีวิต ICIR ในอดีต
2.1 และ 2.2 ทั้งคู่คำนวณค่าเฉลี่ยเลขคณิต และ IC และ ICIR แต่ละตัวในช่วงการทดสอบย้อนหลังจะมีผลเหมือนกันกับปัจจัยตามค่าเริ่มต้น
อย่างไรก็ตาม ในความเป็นจริง ผลกระทบของแต่ละช่วงเวลาของช่วง backtest ต่อช่วงเวลาปัจจุบันนั้นไม่เหมือนกันทุกประการ และมีการลดทอนเวลาด้วย ยิ่งช่วงเวลาใกล้กับช่วงเวลาปัจจุบันมากเท่าใด ผลกระทบก็จะยิ่งมากขึ้นเท่านั้น และยิ่งผลกระทบอยู่ไกลเท่าไรก็ยิ่งน้อยลงเท่านั้น ตามหลักการนี้ ก่อนที่จะคำนวณน้ำหนัก IC ให้กำหนดน้ำหนักครึ่งชีวิตก่อน ยิ่งใกล้กับช่วงเวลาปัจจุบัน ค่าน้ำหนักก็จะยิ่งมากขึ้น และยิ่งห่างออกไป น้ำหนักก็จะยิ่งน้อยลง
ที่มาทางคณิตศาสตร์ของน้ำหนักครึ่งชีวิต:


2.4 เพิ่มน้ำหนัก ICIR สูงสุด
โดยการแก้สมการ ให้คำนวณน้ำหนักตัวประกอบที่เหมาะสมที่สุด w เพื่อเพิ่ม ICIR ให้สูงสุด

ปัญหาการประมาณค่าเมทริกซ์ความแปรปรวนร่วม: เมทริกซ์ความแปรปรวนร่วมใช้เพื่อวัดความสัมพันธ์ระหว่างสินทรัพย์ต่างๆ ในสถิติ เมทริกซ์ความแปรปรวนร่วมตัวอย่างมักใช้แทนเมทริกซ์ความแปรปรวนร่วมประชากร อย่างไรก็ตาม เมื่อขนาดตัวอย่างไม่เพียงพอ เมทริกซ์ความแปรปรวนร่วมตัวอย่างและเมทริกซ์ความแปรปรวนร่วมประชากรจะแตกต่างกันมาก ดังนั้นจึงมีคนเสนอวิธีการประมาณค่าการบีบอัด หลักการคือ การลดค่าคลาดเคลื่อนกำลังสองเฉลี่ยระหว่างเมทริกซ์ความแปรปรวนร่วมที่ประมาณไว้และเมทริกซ์ความแปรปรวนร่วมจริงให้เหลือน้อยที่สุด
ทาง:
1. ตัวอย่างเมทริกซ์ความแปรปรวนร่วม

2. การหดตัวของ Ledoit-Wolf: แนะนำค่าสัมประสิทธิ์การหดตัวเพื่อผสมเมทริกซ์ความแปรปรวนร่วมดั้งเดิมกับเมทริกซ์เอกลักษณ์เพื่อลดผลกระทบของสัญญาณรบกวน

3. การหดตัวโดยประมาณของ Oracle: การปรับปรุงการหดตัวของ Ledoit-Wolf มีเป้าหมายคือการประมาณเมทริกซ์ความแปรปรวนร่วมที่แท้จริงได้แม่นยำยิ่งขึ้น เมื่อขนาดตัวอย่างมีขนาดเล็กโดยการปรับเมทริกซ์ความแปรปรวนร่วม (การดำเนินการเขียนโปรแกรมเหมือนกับการหดตัวของ Ledoit-Wolf)
2.5 PCA การวิเคราะห์องค์ประกอบหลัก
การวิเคราะห์องค์ประกอบหลัก (PCA) เป็นวิธีการทางสถิติที่ใช้เพื่อลดมิติและแยกคุณลักษณะหลักของข้อมูล เป้าหมายคือการแมปข้อมูลต้นฉบับกับระบบพิกัดใหม่ผ่านการแปลงเชิงเส้นเพื่อเพิ่มความแปรปรวนของข้อมูลในระบบพิกัดใหม่ให้สูงสุด
โดยเฉพาะอย่างยิ่ง PCA จะค้นหาองค์ประกอบหลักในข้อมูลก่อน ซึ่งเป็นทิศทางที่มีความแปรปรวนมากที่สุดในข้อมูล จากนั้นจะค้นหาองค์ประกอบหลักตัวที่สองที่ตั้งฉาก (ไม่เกี่ยวข้อง) กับองค์ประกอบหลักตัวแรกและมีความแปรปรวนมากที่สุด กระบวนการนี้ทำซ้ำจนกว่าจะพบองค์ประกอบหลักทั้งหมดในข้อมูล




