이전 장에 이어 다중 요소 모델을 사용하여 강력한 암호화폐 자산 포트폴리오 구축에 관한 기사 시리즈 중 세 가지 기사를 게시했습니다.이론적 기초、데이터 전처리、요인타당성검사。

처음 세 개의 기사에서는 다중 요인 전략 이론과 단일 요인 테스트 단계를 각각 설명합니다.

1. 요인 상관관계 검정을 하는 이유: 다중공선성

단일 요인 테스트를 통해 유효 요인을 일괄 선별하지만 위 요인을 데이터베이스에 직접 입력할 수는 없습니다. 요인 자체는 구체적인 경제적 의미에 따라 넓은 범주로 나눌 수 있으며, 동일한 유형의 요인들 간에는 강한 상관관계가 존재하며, 이를 상관심사 과정 없이 데이터베이스에 직접 입력하고 다중선형회귀분석을 수행하여 기대수익률을 계산하면 다양한 요인에 따라 다중공선성 문제가 발생합니다. 계량경제학에서 다중 공선성은 회귀 모델의 설명 변수 중 일부 또는 전체가 완전하거나 정확한 선형 관계(변수 간 높은 상관 관계)를 갖는다는 것을 의미합니다.

따라서 유효요인을 선별한 후에는 먼저 요인의 주요 항목별 상관관계에 대한 T 검정을 실시하고, 상관관계가 높은 요인에 대해서는 유의성이 낮은 요인을 폐기하거나 요인합성을 수행하는 것이 필요하다.

다중공선성에 대한 수학적 설명은 다음과 같습니다.

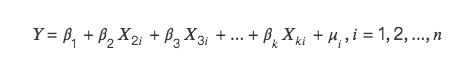
두 가지 상황이 있습니다.

다중 공선성의 결과:

1. 완벽한 공선성에서는 매개변수 추정기가 존재하지 않습니다.

2. OLS 추정기는 대략적인 공선성에서는 유효하지 않습니다.

3. 모수추정기의 경제적 중요성이 불합리하다

4. 변수의 유의성 검정(t 검정)은 유의성을 잃습니다.

5. 모델의 예측 기능이 실패합니다. 다변량 선형 모델에 의해 맞춰진 예측 수익률이 매우 부정확하여 모델이 실패합니다.

2. 1단계: 동일 유형 요인의 상관성 검정

새로 계산된 요인과 이미 데이터베이스에 있는 요인 간의 상관 관계를 테스트합니다. 일반적으로 상관관계 분석에는 두 가지 유형의 데이터가 있습니다.

1. 백테스트 기간 동안 모든 토큰의 팩터 값을 기반으로 상관관계를 계산합니다.

2. 백테스트 기간 동안 모든 토큰의 팩터 초과 수익률 값을 기반으로 상관 관계를 계산합니다.

우리가 추구하는 각 요소는 토큰의 수익률에 대한 특정 기여와 설명력을 가지고 있습니다. 상관관계 테스트**를 수행하는 목적은 전략 수익에 대한 설명과 기여도가 다른 요소를 찾는 것입니다. 전략의 궁극적인 목표는 수익입니다**. 두 팩터가 동일한 수익률을 기술한다면 두 팩터 값이 크게 달라도 의미가 없습니다. 따라서 팩터 값 자체의 차이가 큰 팩터를 찾는 것이 아니라, 수익률을 설명하는 팩터가 서로 다른 팩터를 찾고자 하여 결국 팩터 초과 수익률 값을 이용하여 상관 관계를 계산하기로 결정했습니다.

우리의 전략은 일일 빈도이므로 백테스트 간격의 날짜를 기준으로 팩터 초과 수익률 간의 상관 계수 행렬을 계산합니다.

라이브러리에서 상관관계가 가장 높은 상위 n개 요인을 프로그래밍 방식으로 해결합니다.

def get_n_max_corr(self, factors, n= 1):
       factors_excess = self.get_excess_returns(factors)
       save_factor_excess = self.get_excess_return(self.factor_value, self.start_date, self.end_date)
       if len(factors_excess) < 1:
           return factor_excess, 1.0, None
       factors_excess[self.factor_name] = factor_excess['excess_return']
       factors_excess = pd.concat(factors_excess, axis= 1)
       factors_excess.columns = factors_excess.columns.levels[ 0 ]
       # get corr matrix
       factor_corr = factors_excess.corr()
       factor_corr_df = factor_corr.abs().loc[self.factor_name]
       max_corr_score = factor_corr_df.sort_values(ascending=False).iloc[ 1:].head(n)
       
       return save_factor_excess, factor_corr_df, max_corr_score

3. 2단계: 인자 선택 및 인자 합성

상관관계가 높은 요인 세트의 경우 이를 처리하는 두 가지 방법이 있습니다.

(1) 요인 선정

팩터 자체의 ICIR 값, 수익률, 회전율, 샤프비율을 기준으로 특정 차원에서 가장 효과적인 팩터를 선택하여 유지하고 다른 팩터는 삭제합니다.

(2) 인자합성

요인 집합의 요인을 합성하고 단면에서 가능한 한 많은 효과적인 정보를 유지합니다.

현재 처리할 3가지 요인 행렬이 있다고 가정합니다.

2.1 균등 가중치

각 요소의 가중치는 동일하며(w=1/요인수), 종합요소=각 요소 값의 합을 평균화합니다.

예: 모멘텀 요인, 1개월 수익률, 2개월 수익률, 3개월 수익률, 6개월 수익률, 12개월 수익률 이 6가지 요인의 요인 로딩은 각각 다음을 설명합니다. 가중치의 1/6. , 새로운 운동량 인자 로딩을 합성한 후 다시 정규화를 수행합니다.

종합 1 = 종합.평균(축= 1) # 행별로 평균을 구합니다.

2.2 과거 IC 가중치, 과거 ICIR, 과거 소득 가중치

팩터는 백테스트 기간 동안 IC 값(ICIR 값, 과거 반환 값)에 따라 가중치가 부여됩니다. 과거에는 여러 기간이 있었고 각 기간마다 IC 값이 있으므로 그 평균을 팩터의 가중치로 사용합니다. 백테스트 기간 동안의 IC의 평균(산술 평균)을 가중치로 사용하는 것이 일반적입니다.

2.3 과거 IC 반감기 가중치, 과거 ICIR 반감기 가중치

2.1과 2.2는 모두 산술 평균을 계산하며 백테스트 기간의 각 IC와 ICIR은 기본적으로 요인에 동일한 영향을 미칩니다.

그러나 실제로 백테스트 기간의 각 기간이 현재 기간에 미치는 영향은 정확히 동일하지 않으며 시간 감쇠가 있습니다. 해당 기간이 현재 기간에 가까울수록 영향이 크고, 멀수록 영향이 작습니다. 이 원리에 따라 IC 가중치를 계산하기 전에 먼저 반감기 가중치를 정의하고, 현재 주기에 가까울수록 가중치 값이 커지고 멀어질수록 가중치가 작아집니다.

반감기 체중의 수학적 유도:

2.4 ICIR 가중치 최대화

방정식을 풀어 ICIR을 최대화하는 최적의 요인 가중치 w를 계산합니다.

공분산 행렬 추정 문제: 공분산 행렬은 서로 다른 자산 간의 상관 관계를 측정하는 데 사용됩니다. 통계에서는 모집단 공분산 행렬 대신 표본 공분산 행렬을 사용하는 경우가 많지만, 표본 크기가 부족할 경우 표본 공분산 행렬과 모집단 공분산 행렬이 크게 달라지게 됩니다. 이에 누군가가 압축 추정 방법을 제안했는데, 그 원리는 추정된 공분산 행렬과 실제 공분산 행렬 사이의 평균 제곱 오차를 최소화하는 것입니다.

방법:

1. 샘플 공분산 행렬

2. Ledoit-Wolf 수축: 수축 계수를 도입하여 원래 공분산 행렬과 항등 행렬을 혼합하여 잡음의 영향을 줄입니다.

3. Oracle Approximate Shrinkage: Ledoit-Wolf 수축에 대한 개선으로, 목표는 공분산 행렬을 조정하여 표본 크기가 작을 때 실제 공분산 행렬을 보다 정확하게 추정하는 것입니다. (프로그래밍 구현은 Ledoit-Wolf 수축과 동일합니다)

2.5 주성분 분석 PCA

PCA(Principal Component Analysis)는 데이터의 차원을 줄이고 주요 특징을 추출하는 데 사용되는 통계 방법입니다. 목표는 선형 변환을 통해 원본 데이터를 새 좌표계에 매핑하여 새 좌표계에서 데이터의 분산을 최대화하는 것입니다.

구체적으로 PCA는 먼저 데이터에서 가장 큰 분산이 있는 방향인 주성분을 찾습니다. 그런 다음 첫 번째 주성분과 직교(관련되지 않음)하고 가장 큰 분산을 갖는 두 번째 주성분을 찾습니다. 이 프로세스는 데이터의 모든 주성분을 찾을 때까지 반복됩니다.