LUCIDA:如何利用多因子策略构建强大的加密资产投资组合(因子有效性检验篇)
머리말
이전 책에 이어, 우리는 다중 요소 모델을 사용하여 강력한 암호화 자산 포트폴리오 구축에 관한 기사 시리즈 중 두 개의 기사를 출판했습니다.이론적 기초、데이터 전처리
세 번째 글은 요인 타당성 검정입니다.
특정 요인값을 결정한 후에는 먼저 유의성, 안정성, 단조성, 수익률의 요구사항을 만족하는 요인과 스크린 요인에 대한 타당성 검정을 실시해야 하며, 요인 타당성 검정은 요인 간의 관계를 분석하여 수행합니다. 현재 기간의 가치와 예상 수익률 관계 요인의 타당성을 결정합니다. 주로 3가지 고전적인 방법이 있습니다:
IC/IR 방법: IC/IR 값은 팩터 값과 기대 수익률 간의 상관 계수로 팩터가 클수록 성과가 좋습니다.
T값(회귀법): T값은 현재 기간의 팩터 값에 대해 다음 기간 수익률을 선형회귀한 후 계수의 유의성을 반영하며, 회귀계수가 t 검정을 통과하는지를 비교함으로써 해당 요인의 기여도를 판단할 수 있습니다. 현재 기간의 요인 값을 다음 기간의 수익률로 변환합니다. 일반적으로 다변량(즉, 다요인) 회귀 모델에 사용됩니다.
계층적 백테스팅 방법: 계층적 백테스팅 방법은 요소 값을 기준으로 토큰을 계층화한 다음 각 토큰 계층의 수익률을 계산하여 요소의 단조성을 결정합니다.
1. IC/IR법
(1) IC/IR의 정의
IC: 토큰 수익을 예측하는 요소의 능력을 나타내는 정보 계수입니다. 특정 기간의 IC 값은 현재 기간의 팩터 값과 다음 기간의 수익률 사이의 상관 계수입니다.
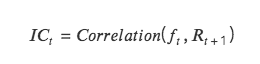

IC가 1에 가까울수록 팩터 값과 다음 기간의 수익률 사이의 양의 상관 관계가 강하다는 것을 의미하며 IC=1은 해당 팩터의 통화 선택이 100% 정확하다는 것을 의미하며 가장 높은 순위 점수를 가진 토큰에 해당합니다. 선택한 토큰은 다음 포지션 조정 주기에 사용됩니다. , 가장 큰 증가;
IC가 -1에 가까울수록 팩터 값과 다음 기간 수익률 사이의 음의 상관관계가 강하다는 의미이며, IC=-1이면 순위가 가장 높은 토큰이 다음 기간에 가장 큰 하락세를 보인다는 의미입니다. 완전한 역전인 재조정 주기 index;
IC가 0에 가까울수록 해당 팩터의 예측력이 극도로 약하다는 의미로, 해당 팩터는 토큰에 대한 예측력이 없음을 의미합니다.
IR: 안정적인 알파를 얻는 요소의 능력을 나타내는 정보 비율입니다. IR은 모든 기간의 평균 IC를 모든 기간의 IC 표준편차로 나눈 값입니다.
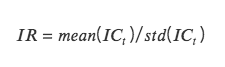
IC의 절대값이 0.05(0.02)보다 크면 해당 팩터의 주식 선택 능력이 강한 것입니다. IR이 0.5보다 크면 해당 팩터는 안정적으로 초과수익을 얻을 수 있는 능력이 강한 것입니다.
(2) IC 계산 방법
일반 IC(피어슨 상관): 가장 고전적인 상관 계수인 피어슨 상관 계수를 계산합니다. 그러나 이 계산 방법에는 데이터가 연속적이고, 정규 분포를 따르며, 두 변수가 선형 관계를 만족한다는 등 많은 가정이 있습니다.
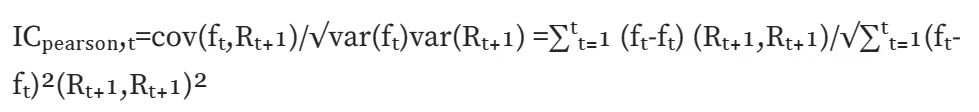
순위 IC(Spearman 순위 상관계수): Spearman 순위 상관계수를 계산하고, 먼저 두 변수를 정렬한 후 정렬된 결과를 바탕으로 Pearson 상관계수를 계산합니다.Spearman의 순위 상관 계수는 두 변수 사이의 단조로운 관계를 평가하며, 정렬된 값으로 변환되므로 데이터 특이치의 영향을 덜 받습니다.Pearson 상관 계수는 원본 데이터에 대한 특정 전제 조건을 가질 뿐만 아니라 데이터 이상값의 영향을 크게 받는 두 변수 간의 선형 관계를 평가합니다. 실제 계산에서는 순위 IC를 찾는 것이 더 일관됩니다.
(3) IC/IR 메소드 코드 구현
날짜 및 시간의 오름차순으로 고유한 날짜 및 시간 값 목록 생성 - 재조정 날짜 기록 def choosedate(dateList, Cycle)
class TestAlpha(object):
def __init__(self, ini_data):
self.ini_data = ini_data
def chooseDate(self, cycle, start_date, end_date):
'''
cycle: day, month, quarter, year
df: 원본 데이터 프레임 df, 날짜 열 처리
'''
chooseDate = []
dateList = sorted(self.ini_data[self.ini_data['date'].between(start_date, end_date)]['date'].drop_duplicates().values)
dateList = pd.to_datetime(dateList)
for i in range(len(dateList)-1):
if getattr(dateList[i], cycle) != getattr(dateList[i + 1 ], cycle):
chooseDate.append(dateList[i])
chooseDate.append(dateList[-1 ])
chooseDate = [date.strftime('%Y-%m-%d') for date in chooseDate]
return chooseDate
def ICIR(self, chooseDate, factor):
# 1. 먼저 각 포지션 조정 날짜의 IC, 즉 ICt를 표시합니다.
testIC = pd.DataFrame(index=chooseDate, columns=['normalIC','rankIC'])
dfFactor = self.ini_data[self.ini_data['date'].isin(chooseDate)][['date','name','price', factor]]
for i in range(len(chooseDate)-1):
# ( 1) normalIC
X = dfFactor[dfFactor['date'] == chooseDate[i]][['date','name','price', factor]].rename(columns={'price':'close 0'})
Y = pd.merge(X, dfFactor[dfFactor['date'] == chooseDate[i+ 1 ]][['date','name','price']], on=['name']).rename(columns={'price':'close 1'})
Y['returnM'] = (Y['close 1'] - Y['close 0']) / Y['close 0']
Yt = np.array(Y['returnM'])
Xt = np.array(Y[factor])
Y_mean = Y['returnM'].mean()
X_mean = Y[factor].mean()
num = np.sum((Xt-X_mean)*(Yt-Y_mean))
den = np.sqrt(np.sum((Xt-X_mean)** 2)*np.sum((Yt-Y_mean)** 2))
normalIC = num / den # pearson correlation
# ( 2) rankIC
Yr = Y['returnM'].rank()
Xr = Y[factor].rank()
rankIC = Yr.corr(Xr)
testIC.iloc[i] = normalIC, rankIC
testIC =testIC[:-1 ]
# 2. ICt를 기준으로 [IC_Mean, IC_Std,IR,IC를 찾습니다.<0 비율--계수 방향,-IC->0.05 비율]
'''
ICmean: |IC|>0.05,팩터는 코인을 선택하는 강력한 능력을 가지고 있으며, 팩터 값은 다음 기간의 수익률과 높은 상관관계를 가지고 있습니다. -IC-<0.05,팩터의 통화선택능력이 약하고 팩터값과 차기수익률의 상관관계가 낮다.
IR: |IR|>0.5,요소 통화 선택 능력이 강력하고 IC 가치가 상대적으로 안정적입니다. -IR-<0.5,IR 값이 너무 작아서 요인이 그다지 효과적이지 않습니다. 0에 가까우면 기본적으로 무효입니다.
IClZero (IC less than Zero): IC<0이 거의 절반을 차지 -> 팩터 중립 IC>0이 절반을 초과하는 것은 마이너스 팩터, 즉 팩터 값이 커질수록 수익률은 감소
ICALzpF(IC abs large than zero poin five): |IC|>0.05의 비율이 높은 편에 있어 대부분의 요인이 효과적임을 나타냅니다.
'''
IR = testIC.mean()/testIC.std()
IClZero = testIC[testIC<0 ].count()/testIC.count()
ICALzpF = testIC[abs(testIC)>0.05 ].count()/testIC.count()
combined =pd.concat([testIC.mean(), testIC.std(), IR, IClZero, ICALzpF], axis= 1)
combined.columns = ['ICmean','ICstd','IR','IClZero','ICALzpF']
#3.리밸런싱 기간 동안 IC의 IC 누적 차트
print("Test IC Table:")
print(testIC)
print("Result:")
print('normal Skewness:', combined['normalIC'].skew(),'rank Skewness:', combined['rankIC'].skew())
print('normal Skewness:', combined['normalIC'].kurt(),'rank Skewness:', combined['rankIC'].kurt())
return combined, testIC.cumsum().plot()
2. T-값 검정(회귀법)
T값법도 당기의 팩터값과 차기의 수익률과의 관계를 검정하는데, 둘 사이의 상관관계를 분석하는 점에서 ICIR법과 다르다. 종속변수 Y로, 현재 기간의 요인 값을 독립변수 X로 반환합니다. X 회귀의 경우 회귀 요인 값의 회귀계수에 대해 t 검정을 수행하여 0과 유의하게 다른지, 즉 현재 기간 요소는 다음 기간의 수익률에 영향을 미칩니다.
이 방법의 핵심은 이변량 회귀 모델을 해결하는 것이며 구체적인 공식은 다음과 같습니다.
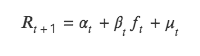

(1) 회귀방법론

(2) 회귀 메소드 코드 구현
def regT(self, chooseDate, factor, return_ 24 h):
testT = pd.DataFrame(index=chooseDate, columns=['coef','T'])
for i in range(len(chooseDate)-1):
X = self.ini_data[self.ini_data['date'] == chooseDate[i]][factor].values
Y = self.ini_data[self.ini_data['date'] == chooseDate[i+ 1 ]][return_ 24 h].values
b, intc = np.polyfit(X, Y,1) # 경사
ut = Y - (b * X + intc)
# t 값 찾기 t = (\hat{b} - b) / se(b)
n = len(X)
dof = n - 2 # 자유도
std_b = np.sqrt(np.sum(ut** 2) / dof)
t_stat = b / std_b
testT.iloc[i] = b, t_stat
testT = testT[:-1 ]
testT_mean = testT['T'].abs().mean()
testT L1 96 = len(testT[testT['T'].abs() > 1.96 ]) / len(testT)
print('testT_mean:', testT_mean)
print(1.96보다 큰 T 값의 비율:, testT L1 96)
return testT
3. 계층화된 백테스팅 방법
계층화는 모든 토큰을 계층화하는 것을 의미하고, 백테스팅은 토큰 조합의 각 계층의 반환율을 계산하는 것을 의미합니다.
(1) 계층화
먼저, 토큰 풀에 해당하는 팩터 값을 구하고, 팩터 값에 따라 토큰을 정렬합니다. 오름차순으로 정렬합니다. 즉, 요소 값이 작은 것이 먼저 순위를 매기고, 정렬에 따라 토큰을 균등하게 나눕니다. 레이어 0 토큰의 요소 값이 가장 작고, 레이어 9 토큰의 요소 값이 가장 큽니다.
이론적으로 균등 분할은 토큰 수를 균등하게 분할하는 것을 의미합니다. 즉, 각 계층의 토큰 수는 동일하며 이는 분위수의 도움으로 달성됩니다. 실제로 토큰의 총 개수는 반드시 레이어 수의 배수가 아닙니다. 즉, 각 레이어의 토큰 수가 반드시 동일하지는 않습니다.
(2) 백테스팅
토큰을 팩터 값의 오름차순으로 10개 그룹으로 나눈 후, 각 토큰 조합의 수익률 계산을 시작합니다. 이 단계에서는 각 계층의 토큰을 투자 포트폴리오로 취급하고(각 계층의 토큰 조합에 포함된 토큰은 서로 다른 백테스트 기간 동안 변경됨) 포트폴리오의 전체 가치를 계산합니다.다음 기간의 수익률. ICIR과 t값은 현재 요인값을 분석하여다음 기간의 전체 수익률, 그러나 계층화된 백테스팅에는 계산이 필요합니다.백테스트 기간 동안 거래일별 계층화 포트폴리오 수익률. 여러 기간의 백테스팅 기간이 있으므로 각 기간마다 계층화 및 백테스팅이 필요합니다. 마지막으로 각 계층의 토큰 반환율을 누적 곱하여 토큰 조합의 누적 반환율을 계산합니다.
이상적으로는 좋은 팩터의 경우 그룹 9의 곡선 수익률이 가장 높고 그룹 0의 곡선 수익률이 가장 낮습니다.
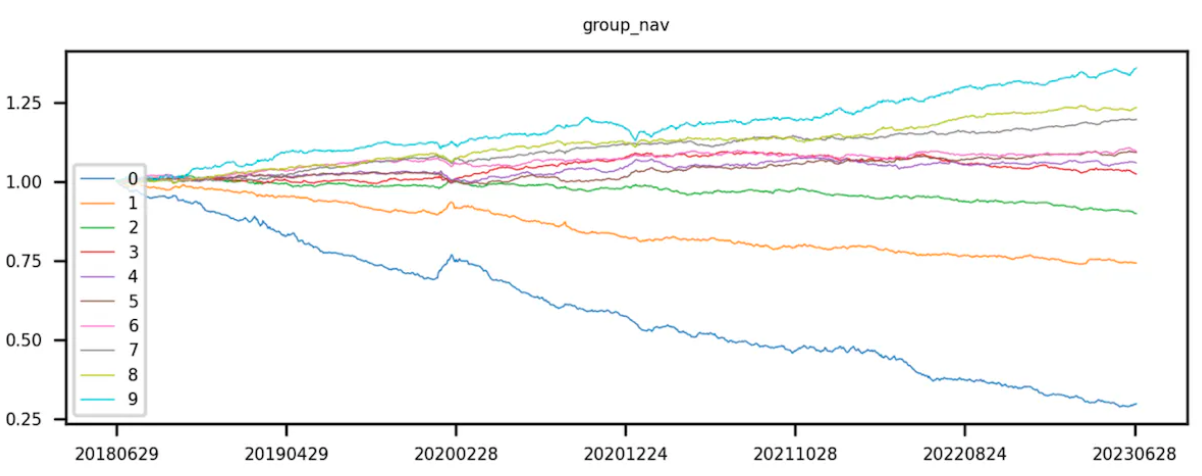
그룹 9에서 그룹 0(즉, 롱-숏 수익률)을 뺀 곡선은 단조롭게 증가합니다.
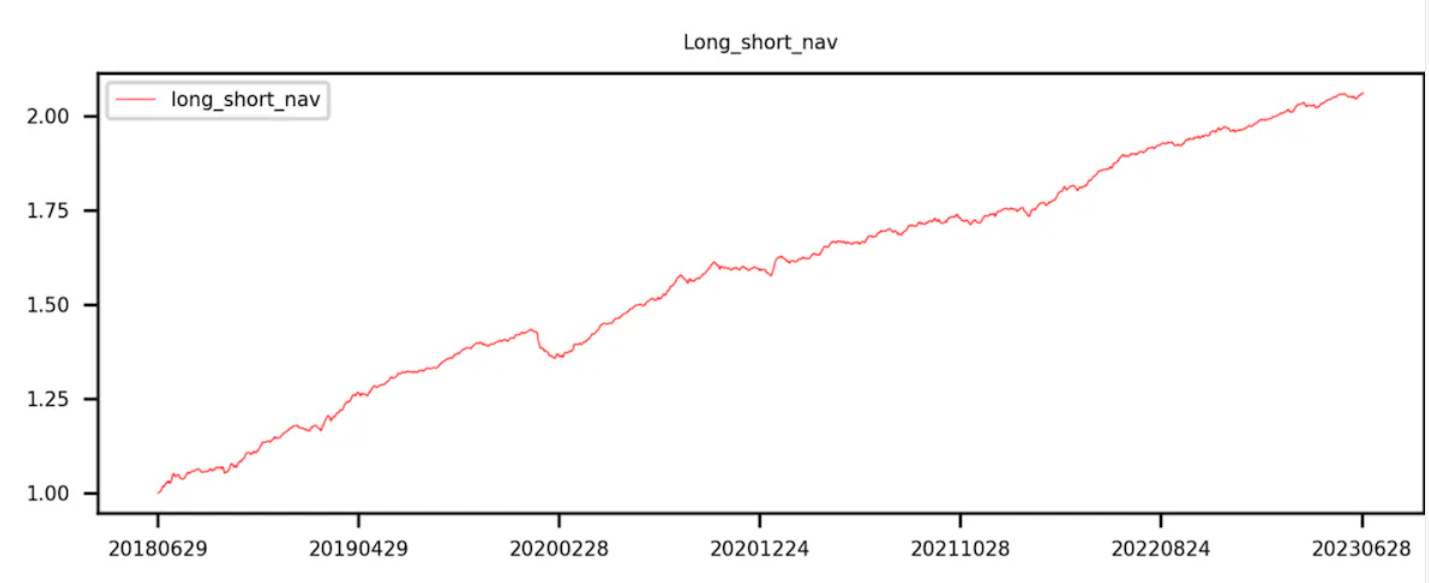
(3) 계층적 백테스팅 방법의 코드 구현
def layBackTest(self, chooseDate, factor):
f = {}
returnM = {}
for i in range(len(chooseDate)-1):
df 1 = self.ini_data[self.ini_data['date'] == chooseDate[i]].rename(columns={'price':'close 0'})
Y = pd.merge(df 1, self.ini_data[self.ini_data['date'] == chooseDate[i+ 1 ]][['date','name','price']], left_on=['name'], right_on=['name']).rename(columns={'price':'close 1'})
f[i] = Y[factor]
returnM[i] = Y['close 1'] / Y['close 0'] -1
labels = ['0','1','2','3','4','5','6','7','8','9']
res = pd.DataFrame(index=['0','1','2','3','4','5','6','7','8','9','LongShort'])
res[chooseDate[ 0 ]] = 1
for i in range(len(chooseDate)-1):
dfM = pd.DataFrame({'factor':f[i],'returnM':returnM[i]})
dfM['group'] = pd.qcut(dfM['factor'], 10, labels=labels)
dfGM = dfM.groupby('group').mean()[['returnM']]
dfGM.loc[LongShort] = dfGM.loc[0]- dfGM.loc[9]res[chooseDate[i+ 1 ]] = res[chooseDate[ 0 ]] * ( 1 + dfGM[returnM ]) data = pd.DataFrame({계층적 누적 반환:res.iloc[: 10,-1],그룹:[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ]})
df 3 = data.corr()
print("Correlation Matrix:")
print(df 3)
return res.T.plot(title='Group backtest net worth curve')



