Curve Stablecoin 설계 백서(중국어 및 영어 참조 버전)

첫 번째 레벨 제목Curve Finance

원본 편집:JamesX，iZUMi Research

Overview

The design of the stablecoin has few concepts: lending-liquidating amm algorithm (LLAMMA), PegKeeper, Monetary Policy are the most important ones. But the main idea is in LLAMMA: replacing liquidations with a special-purpose AMM.

이미지 설명

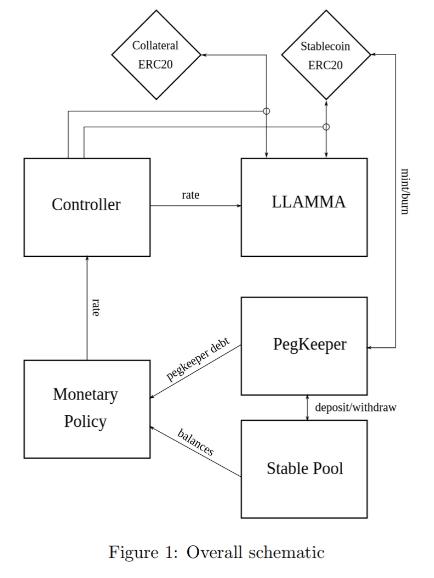
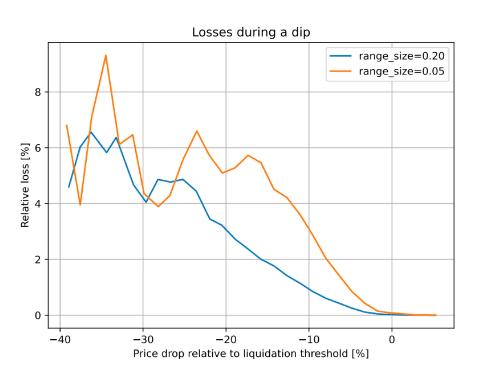
Figure 2 : Dependence of the loss on the price shift relative to the liquidation threshold. Time window for the observation is 3 days

텍스트

In this design, if someone borrows against collateral, even at liquidation threshold, and the price of collateral dips and bounces - no significant loss happen. For example, according to simulations using historic data for ETH/USD since Sep 2017 , if one leaves the CDP unattended for 3 days and during this time the price drop of 10% below the liquidation threshold happened - only 1% of collateral gets lost.

보조 제목

AMM for continuous liquidation/deliquidation (LLAMMA)

지속적인 청산/청산 없는 AMM(LLAMMA)

The core idea of the stablecoin design is Lending-Liquidating AMM Algorithm. The idea is that it converts between collateral (for example, ETH) and the stablecoin (let’s call it USD here). If the price of collateral is high - a user has deposits all in ETH, but as it goes lower, it converts to USD. This is very different from traditional AMM designs where one has USD on top and ETH on the bottom instead.

스테이블 코인 설계의 핵심 아이디어는 Lending-Liquidating AMM 알고리즘입니다. 아이디어는 담보(예: ETH)와 스테이블 코인(여기서는 USD라고 부름) 사이에서 전환된다는 것입니다. 담보 가격이 높으면 사용자 예치금은 모두 ETH로, 가격이 낮으면 USD 스테이블 코인으로 전환됩니다. 이것은 전통적인 AMM 설계와 매우 다릅니다.전통적인 AMM 설계는 USD 스테이블 코인을 상단(AMM 곡선의 위쪽 절반)에, ETH를 아래쪽(AMM 곡선의 아래쪽 절반)에 배치하는 것입니다.

The below description doesn’t serve as fully self-consistent rigorous proofs. A lot of that (especially the invariant) are obtained from dimensional considerations. More research might be required to have a full mathematical description, however the below is believed to be enough to implement in practice.

다음 설명은 완전히 자체적으로 일관된 엄격한 증거로 사용되지 않습니다. 많은 것(특히 불변량)이 다양한 차원에서 고려됩니다. 완전한 수학적 설명을 얻으려면 더 많은 연구가 필요할 수 있지만 아래 설명은 스마트 계약의 구현을 지원하기에 충분하다고 간주됩니다.

This is only possible with an external price oracle. In a nutshell, if one makes a typical AMM (for example with a bonding curve being a piece of hyperbola) and ramps its “center price” from (for example) down to up, the tokens will adiabatically convert from (for example) USD to ETH while proving liquidity in both ways on the way (Fig. 3 ). It is somewhat similar to avoided crossing (also called Landau-Zener transition) in quantum physics (though only as an idea: mathematical description of the process could be very different). The range where the liquidity is concentrated is called band here, at the constant po band has liquidity from pcd to pcu. We seek for pcd(po) and pcu(po) being functions of po only, functions being more steep than linear and, hence, growing faster than po(Fig. 4 ). In addition, let’s defifine prices p↓and p↑ being prices where p↓(po) = po, and p↑(po) = po, defining ends of bands in adiabatic limit (e.g. p = po).

이는 외부 오라클의 가격 피드를 통해서만 가능합니다. 요컨대, 일반적인 AMM(예를 들어 결합 곡선은 쌍곡선의 조각임)을 취하고 다음을 입력합니다."센터 가격"(예를 들어) 아래에서 위로 이동하기 위해 토큰은 (예를 들어) USD에서 ETH로 "단열적으로" 변환되는 동시에 프로세스에서 양방향으로 유동성을 제공합니다(그림 3). 이것은 양자 물리학의 "교차 방지"(Landau-Zener 전이라고도 함)와 다소 유사합니다(개념일 뿐: 과정의 수학적 설명은 매우 다를 수 있음).

이미지 설명

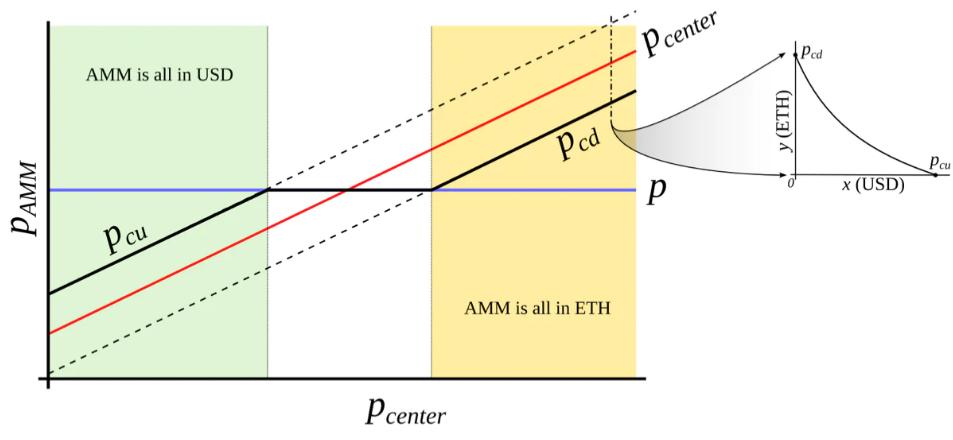Figure 3 : Behavior of an “AMM with an external price source”. External price pcenter determines a price around which liquidity is formed. AMM supports liquidity concentrated from prices pcd to pcu, pcd < pcenter < pcu. When current price p is out of range between pcd and pcu, AMM is either fully in stablecoin (when at pcu) or fully in collateral (when at pcd). When pcd ≤ p ≤ pcu, AMM price is equal to the current price p.

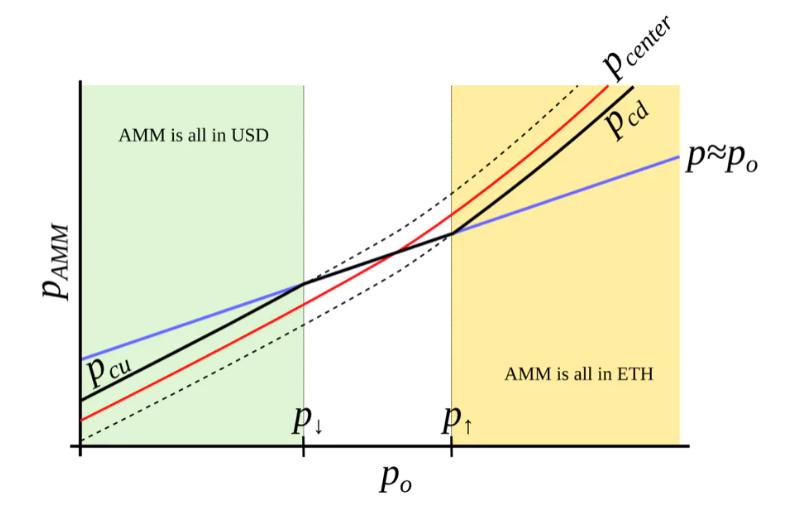Figure 4 : AMM which we search for. We seek to construct an AMM where pcd and pcu are such functions of po that when po grows, they grow even faster. In this case, this AMM will be all in ETH when ETH is expensive, and all in USD when ETH is cheap.

We start from a number of bands where, similarly to Uniswap 3 , hyperbolic shape of the bonding curve is preserved by adding virtual balances. Let say, the amount of USD is x, and the amount of ETH is y, therefore the “amplifified” constant-product invariant would be:

결합 곡선의 쌍곡선 모양을 유지하면서 "가상 균형"을 추가하여 Uniswap 3과 유사한 일부 밴드로 시작합니다. USD 금액이 x이고 ETH 금액이 y라고 가정해 보겠습니다."향상된"상수 - 제품 불변은 다음과 같습니다.

We also can denote x 0 ≡ x  +  f and y 0 ≡ y + g so that the invariant can be written as a familiar I =  x 0 y 0. However, f and g do not stay constant: they change with the external price oracle (and so does the invariant I, so it is only the invariant while the oracle price po is unchanged). At a given po, f and g are constant across the band. As mentioned before, we denote p↑ as the top price of the band and p↓as the bottom price of the band. We defifine A (a measure of concentration of liquidity) in such a way that:

또한 x 0 ≡x+f 및 y 0 ≡y+g를 표현할 수 있으므로 불변량은 친숙한 I=x 0 y 0 으로 쓸 수 있습니다. 그러나 f와 g는 일정하지 않습니다. 외부 오라클 가격이 변경되면 변경됩니다(불변량 I도 마찬가지이므로 오라클 가격 po가 일정할 때만 불변합니다). 주어진 po에서 f와 g는 대역 전체에서 일정합니다. 이전과 마찬가지로 p↑를 밴드의 최고 가격으로, p↓를 밴드의 최저 가격으로 표시합니다. A(유동성 집중 측정)의 정의는 다음과 같습니다.

The property we are looking for is such that higher price po should lead to even higher price at the same balances, so that the current market price (which will, on average, follow po) is lower than that, and the band will trade towards being all in ETH (and the opposite is also true for the other direction). It is possible to find many ways to satisfy that but we need one:

우리가 찾고 있는 속성은 다음과 같습니다: 더 높은 가격 po는 동일한 잔액에 대해 더 높은 가격으로 이어져야 하므로 현재 시장 가격(평균적으로 po를 따를 것임)은 이 가격보다 낮고 밴드는 다음으로 이동합니다. ETH의 방향(다른 방향도 마찬가지). 만족할 수 있는 방법은 여러 가지가 있지만 이 방법이 필요합니다.

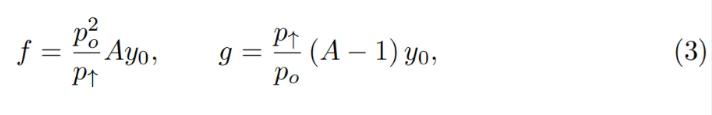
where y 0 is a p 0 -dependent measure of deposits in the current band, denominated in ETH, defifined in such a way that when current price p, p↑ and po are equal to each other, then y = y 0 and x = 0 (see the point at po = p↑ on Fig. 4 ). Then if we substitute y at that moment:

그 중 y 0은 현재 밴드 예치금을 측정하기 위한 p 0과 관련된 지표로 ETH에 있으며 그 정의는 현재 가격 p, p↑ 및 po가 서로 같을 때 y=y 0 , x=0(그림 4의 po=p↑ 지점 참조). 따라서 그 순간에 y를 바꾸면:

Price is equal to dx 0 /dy 0 which then for a constant-product invariant is:

가격이 dx 0 /dy 0 이면 상수 제품 불변량의 경우 다음과 같습니다.

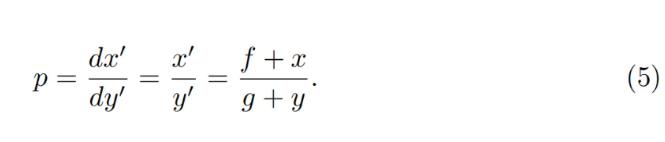
One can substitute situations where po = p↑ or po = p↓ with x = 0 or y = 0 correspndingly to verify that the above formulas are self-consistent.

x=0 또는 y=0을 사용하여 po=p↑ 또는 po=p↓를 대체하여 위의 공식이 자체 일관성이 있는지 확인할 수 있습니다.

Typically for a band, we know p↑ and, hence, p↓, po, constant A, and also x and y (current deposits in the band). To calculate everything, we need to find yo. It can be found by solving the quadratic equation for the invariant:

일반적으로 밴드의 경우 p↑, 따라서 p↓, po, 상수 A, x 및 y(밴드의 현재 예치금)를 알고 있습니다. 나머지를 계산하려면 요를 찾아야 합니다. 불변량에 대한 이차 방정식을 풀면 다음과 같이 구할 수 있습니다.

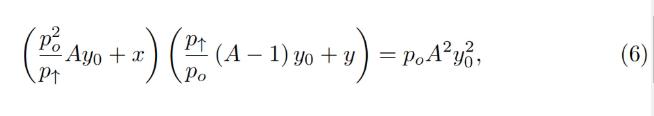
which turns into the quadratic equation against yo:

이것은 요에 대한 이차 방정식이 됩니다:

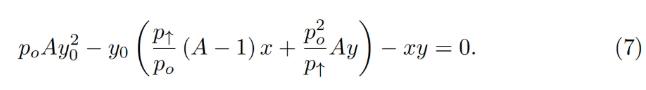
In the smart contract, we solve this quadratic equation in get_y 0 function.

스마트 계약에서는 get_y 0 함수에서 이 이차 방정식을 풉니다.

While oracle price po stays constant, the AMM works in a normal way, e.g. sells ETH when going up / buys ETH when going down. By simply substituting x = 0 for the “current down” price pcd or y = 0 for the “current up” price pcu values into the equation of the invariant respectively, it is possible to show that AMM prices at the current value of po and the current value of p↑ are:

오라클 가격이 일정하게 유지되면 AMM은 정상적인 방식으로 작동합니다(예: ETH가 오를 때 매도/내릴 때 ETH 매수). 단순히 x=0을"현재 드롭"pcd 또는 y=0의 가격은 다음으로 대체됩니다."전류 상승"p의 가격의 pcu 값을 불변 방정식에 각각 대입하면 현재 po의 값과 p↑의 현재 값에서 AMM 가격이 다음과 같이 표시될 수 있습니다.

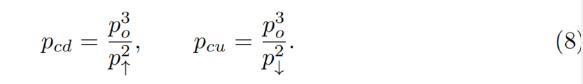
Another practically important question is: if price changes up or down so slowly that the oracle price po is fully capable to follow it adiabatically, what amount y↑ of ETH (if the price goes up) or x↓ of USD (if the price goes down) will the band end up with, given current values x and y and that we start also at p = po. While it’s not an immediately trivial mathematical problem to solve, numeric computations showed a pretty simple answer:

또 다른 중요한 실제 질문: 가격이 너무 느리게 변하여 오라클 가격 po가 완벽하게 "단열적으로"(대역 내에서) 따라갈 수 있는 경우 현재 값 x 및 y가 주어지고 p=po일 때부터 시작합니다. 시작하면 ETH의 y↑(가격이 오르는 경우) 또는 USD의 x↓(가격이 내려가는 경우)가 이 밴드를 얻게 됩니다. 이것은 즉시 해결할 수 있는 수학적 문제는 아니지만 수치 계산을 통해 매우 간단한 답을 얻을 수 있습니다.

We will use these results when evaluating safety of the loan as well as the potential losses of the AMM.

우리는 대출의 안전성과 AMM의 잠재적 손실을 평가할 때 이 결과를 사용할 것입니다.

Now we have a description of one band. We split all the price space into bands which touch each other with prices p↓ and p↑ so that if we set a base price pbase and have a band number n:

이제 밴드에 대한 설명이 있습니다. 우리는 모든 가격 공간을 가격 p↓와 p↑가 서로 닿는 밴드로 나눕니다. 따라서 기본 가격 pbase를 밴드 번호 n으로 설정하면:

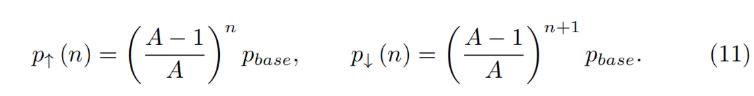
It is possible to prove that the solution of Eq. 7 and Eq. 5 for any band gives:

모든 대역에 대해 방정식 7과 방정식 5의 솔루션을 얻을 수 있음을 알 수 있습니다.

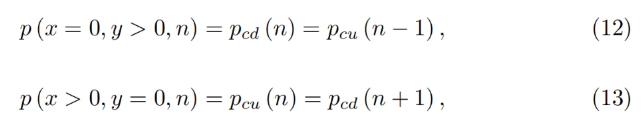
which shows that there are no gaps between the bands.

이것은 밴드 사이에 간격이 없음을 보여줍니다.

Trades occur while preserving the invariant from Eq. 1 , however the current price inside the AMM shifts when the price po: it goes up when po goes down and vice versa cubically, as can be seen from Eq. 8.

첫 번째 레벨 제목

LLAMMA vs Stablecoin

Stablecoin is a CDP where one borrows stablecoin against a volatile collateral (cryptocurrency, for example, against ETH). The collateral is loaded into LLAMMA in such a price range (such bands) that if price of collateral goes down relatively slowly, the ETH gets converted into enough stablecoin to cover closing the CDP (which can happen via a self-liquidation, or via an external liquidation if the coverage is too close to dangerous limits, or not close at all while waiting for the price bounce).

Stablecoins는 사람들이 휘발성 담보(ETH와 같은 암호화폐)에 대해 빌린 일종의 CDP입니다. 담보는 LLAMMA의 가격 범위(이러한 밴드)에 로드되며, 담보 가격이 상대적으로 천천히 떨어지면 ETH는 CDP 마감을 충당하기에 충분한 스테이블코인으로 변환됩니다(이는 자기 청산 또는 외부 청산을 통해 발생할 수 있습니다. 가격이 반등하기를 기다리는 동안 모기지 금리가 위험한 한도에 너무 가깝거나 전혀 닫히지 않은 경우).

When a user deposits collateral and borrows a stablecoin, the LLAMMA smart contract calculates the bands where to locate the collateral.  When the price of the collateral changes, it starts getting converted to the stablecoin. When the system is “underwater”, user already has enough USD to cover the loan. The amount of stablecoins which can be obtained can be calculated using a public get_x_down method. If it gives values too close to the liquidation thresholds - an external liquidator can be involved (typically shouldn’t happen within a few days or even weeks after the collateral price went down and sideways, or even will not happen ever if collateral price never goes up or goes back up relatively quickly). A health method returns a ratio of get_x_down to debt plus the value increase in collateral when the price is well above “liquidation”.

사용자가 담보를 예치하고 스테이블 코인을 빌릴 때 LLAMMA 스마트 계약은 담보가 어느 밴드에 있는지 계산합니다. 담보 가격이 변경되면 스테이블 코인으로 전환되기 시작합니다. 시스템이 있을 때"수중", 사용자는 이미 대출금을 지불하기에 충분한 USD를 가지고 있습니다. 얻을 수 있는 스테이블 코인의 양은 공개된 get_x_down 메소드를 통해 계산할 수 있습니다. 청산 임계값에 너무 가까운 값을 제공하는 경우 외부 청산인이 개입할 수 있습니다(보통 담보 가격이 상승하지 않거나 상대적으로 더 빠르더라도 담보 가격이 하락하고 횡보한 후 며칠 또는 몇 주 내에 발생해서는 안 됨) 픽업, 절대 일어나지 않을 것입니다). 가격이 훨씬 높을 때"청산하다", 건전한 방법은 부채에 대한 get_x_down의 비율과 담보 가치의 증가를 반환합니다.

When a stablecoin charges interest, this should be reflected in the AMM, too. This is done by adjusting all the grid of prices. So, when a stablecoin charges interest rate r, all the grid of prices in the AMM shifts upwards with the same rate r which is done via a base_price multiplier. So, the multiplier goes up over time as long as the charged rate is positive.

스테이블 코인이 이자를 부과할 때 AMM에 반영되어야 합니다. 반영도 해야 합니다. 이것은 가격에 대한 모든 그리드를 조정함으로써 달성됩니다. 따라서 스테이블 코인이 이자율 r을 부과하면 AMM의 모든 가격은 동일한 이자율 r로 상승하며 이는 기본 가격 승수를 통해 이루어집니다. 따라서 요금이 양수인 한 승수는 시간이 지남에 따라 올라갑니다.

When we calculate get_x_down or get_y_up, we are first looking for the amounts of stablecoin and collateral x∗ and y∗ if current price moves to the current price po. Then we look at how much stablecoin or collateral we get if po adiabatically changes to either the lowest price of the lowest band, or the highest price of the highest band respectively. This way, we can get a measure of how much stablecoin we will which is not dependent on the current instantaneous price, which is important for sandwich attack resistance.

get_x_down 또는 get_y_up을 계산할 때 현재 가격이 현재 가격 po로 이동하는 경우 가장 먼저 찾는 것은 stablecoin과 담보 x∗ 및 y∗의 양입니다. 그런 다음 po가 가장 낮은 범위에서 가장 낮은 가격 또는 가장 높은 범위에서 가장 높은 가격으로 단열적으로 변경되면 각각 얼마나 많은 스테이블 코인 또는 담보를 받는지 확인합니다. 이런 식으로 우리는 메자닌 공격의 저항에 중요한 현재 순간 가격에 의존하지 않는 스테이블 코인을 얼마나 얻을 수 있는지에 대한 척도를 얻을 수 있습니다. **
**

It is important to point out that the LLAMMA uses po defined as ETH/USD price as a price source, and our stablecoin could be traded under the peg (ps < 1 ) or over peg (ps > 1 ). If ps < 1 , then price in the LLAMMA is p > po.

LLAMMA는 ETH/USD의 가격으로 정의된 po를 가격 소스로 사용하며 당사의 스테이블 코인은 페그 아래(ps<1) 또는 위(ps>1)에서 거래될 수 있습니다. 추신 경우<1이면 LLAMMA의 가격은 p>po입니다.

In adiabatic approximation, p = po/ps, and all the collateral<>stablecoin conversion would happen at a higher oracle price / as if oracle price was lower and equal to:

단열 근사에서 p=po/ps, 모든 담보<>Stablecoin 변환은 오라클 가격이 더 낮고 다음과 같은 경우 더 높은 오라클 가격에서 발생합니다.

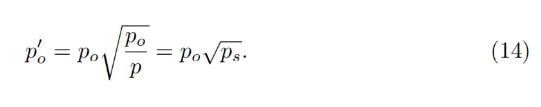
At this price, the amount of stablecoins obtained at conversion is higher by factor of 1/ps (if ps < 1 ) .

이 가격에서 전환 시 획득하는 스테이블 코인의 수는 1/ps의 계수만큼 더 높습니다(ps인 경우<1 ）。

It is less desirable to have ps > 1 for prolonged times, and for that we will use the stabilizer (see next)

자동 안정 장치 및 통화 정책

Automatic Stabilizer and Monetary Policy

자동 안정 장치 및 통화 정책

When ps > 1 (for example, because of the increased demand for stablecoin), there is peg-keeping reserve formed by an asymmetric deposit into a stableswap Curve pool between the stablecoin and a redeemable reference coin or LP token. Once ps > 1 , the PegKeeper contract is allowed to mint uncollateralized stablecoin and (only!) deposit it to the stableswap pool single-sided in such a way that the final price after this is still no less than 1. When ps < 1 , the PegKeeper is allowed to withdraw (asymmetrically) and burn the stablecoin.

ps > 1인 경우(예: 스테이블 코인에 대한 수요 증가로 인해) 스테이블 코인과 상환 가능한 참조 코인 또는 LP 토큰 사이의 비대칭 예치금에 의해 스테이블 스왑 곡선 풀에 페깅된 준비금이 있습니다. 일단 ps>1이면 PegKeeper 계약은 무담보 스테이블 코인을 발행하고 한쪽 스테이블 스왑 풀에만 예치할 수 있으며 그렇게 한 후에도 최종 가격은 여전히 ​​1보다 낮지 않습니다. ps 때< 1, PegKeeper는 스테이블 코인을 인출(비대칭)하고 소각할 수 있습니다.

These actions cause price ps to quickly depreciate when it’s higher than 1 and appreciate if lower than 1 because asymmetric deposits and withdrawals change the price. Even though the mint is uncollateralized, the stablecoin appears to be implicitly collateralized by liquidity in the stablecoin pool. The whole mint/burn cycle appears, at the end, to be profitable while providing stability.

이러한 행동으로 인해 가격 ps는 비대칭 예금 및 인출로 인해 가격이 변경됨에 따라 1 이상으로 급격히 하락하고 1 이하로 상승합니다. "민팅"의 이 부분은 담보가 없지만 스테이블 코인은 스테이블 코인 풀에서 유동성의 암시적 담보로 뒷받침되는 것으로 보입니다. 전체 주조/소각 주기는 안정성을 제공하면서 결국에는 수익성이 있는 것으로 보입니다.

Let’s denote the amount of stablecoin minted to the stabilizer (debt) as dst and the function which calculates necessary amount of redeemable USD to buy the stablecoin in a stableswap AMM get_dx as fdx(). Then, in order to keep reserves not very large, we use the “slow” mechanism of stabilization via varying the borrow r:

스테이블코인(부채)에 발행된 스테이블코인의 양을 dst로 표시하고 스테이블스왑 AMM get_dx에서 스테이블코인을 구매하는 데 필요한 상환 가능한 USD 금액을 계산하는 함수를 fdx()로 표시해 보겠습니다. 그런 다음 "예비"가 너무 커지지 않도록 다음을 사용합니다."느린"안정화 메커니즘.

where h is the change in ps at which the rate r changes by factor of 2 (higher ps leads to lower r). The amount of stabilizer debt dst will equilibrate at different value depending on the rate at ps = 1 r 0. Therefore, we can (instead of setting manually) be reducing r 0 while dst/supply is larger than some target number (for example, 5%) (thereby incentivizing borrowers to borrow-and-dump the stablecoin, decreasing its price and forcing the system to burn the dst) or increasing if it’s lower (thereby incentivizing borrowers to return loans and pushing ps up, forcing the system to increase the debt dst and the stabilizer deposits).

첫 번째 레벨 제목

결론/요약

The presented mechanisms can, hopefully, solve the riskiness of liquidations for stablecoin-making and borrowing purposes. In addition, stabilizer and automatic monetary policy mechanisms can help with peg-keeping without the need of keeping overly big PSMs.

제안된 메커니즘이 스테이블 코인 발행 및 대출 목적을 위한 청산의 위험한 특성을 해결할 수 있기를 바랍니다. 또한 안정 장치와 자동 통화 정책 메커니즘은 과도한 PSM(Peg Stability Module anchor stability module)을 유지할 필요 없이 가격 앵커를 유지하는 데 도움이 될 수 있습니다.