LUCIDA:如何利用多因子策略构建强大的加密资产投资组合(因子正交化篇)
前章に引き続き、「多要素モデルを使用した強力な暗号資産ポートフォリオの構築」に関する一連の記事を 4 回公開しました。「理論の基礎」、「データの前処理」、「因子妥当性テスト」、「大分類因子分析:因子総合」。
前回の記事では、因子の共線性(因子間の相関が高い)の問題について詳しく説明しましたが、大きなカテゴリーの因子を合成する前に、因子の直交化を行って共線性を解消する必要があります。

1. 因子直交化の数学的導出
多因子断面回帰の観点から、因子直交系が確立されます。

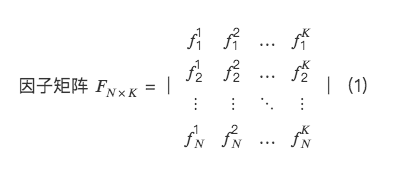

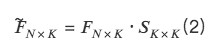

それで、
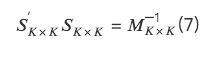



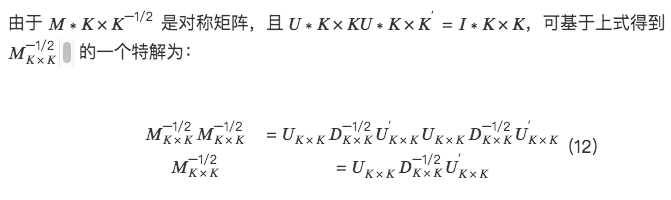



2. 3 つの直交手法の具体的な実装
1.シュミット直交性




シュミット直交法は逐次直交法であるため、因子直交性の次数を決定する必要があります。一般的な直交次数には、固定次数(異なるセクションで同じ直交次数がとられる)と動的次数(各セクションで同じ直交次数がとられる)があります。直交順序は一定のルールに従って決定されます)。シュミット直交法の利点は、同じ次数の直交因子間に明示的な対応関係があることですが、直交次数に対する統一された選択基準はなく、直交化後のパフォーマンスは直交次数基準やウィンドウ期間に影響される可能性があります。パラメーター。 。

2.正規直交性

 # Canonical 直交 def Canonical(self):
# Canonical 直交 def Canonical(self):
overlapping_matrix = (time_tag_data.shape[ 1 ] - 1) * np.cov(time_tag_data.astype(float))
# 固有値と固有ベクトルを取得
eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix)
# np で行列に変換
eigenvector = np.mat(eigenvector)
transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5))))
orthogonalization = np.dot(time_tag_data.T.values, transition_matrix)
orthogonalization_df = pd.DataFrame(orthogonalization.T, index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]), columns=time_tag_data.columns)
self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)
3. 対称直交
シュミット直交では、過去のいくつかのセクションで同じ直交順序の因子が採用されるため、直交因子と元の因子の間には明示的な対応関係が存在しますが、正準直交では各セクションの主成分が選択されます。直交性の前後で因子間の安定した対応関係。直交組み合わせの効果は、直交前後の因子間に安定した対応関係があるかどうかに大きく依存することがわかります。
対称直交性では、元の因子行列への変更を可能な限り減らして、一連の直交基底を取得します。これにより、直交因子と因果因子との間の類似性を最大限に維持することができる。また、シュミットの直交法のように、直交順序の早い方の因子を優先することは避けてください。

対称直交特性:
シュミット直交と比較すると、対称直交は直交順序を与える必要がなく、各要素を同等に扱います。
すべての直交遷移行列の中で、対称直交行列と元の行列の間の類似度が最も大きく、つまり、前後の直交行列間の距離が最も小さくなります。




