インタラクティブな証明を非インタラクティブな証明に変換するにはどうすればよいでしょうか?
序文
序文
暗号化におけるゼロ知識証明テクノロジーは、プライベート コンピューティング、zkRollup などを含む、Web3 の世界に幅広い用途があります。このうち、レイヤ 2 プロジェクト FOX で使用されている FOAKS は、ゼロ知識証明アルゴリズムです。上述の一連のアプリケーションの中で、ゼロ知識証明アルゴリズムにとって非常に重要な特性は、アルゴリズムの効率性と対話性という 2 つです。
アルゴリズムの効率の重要性は自明です。効率的なアルゴリズムはシステムの実行時間を大幅に短縮し、それによってクライアントの待ち時間が短縮され、ユーザー エクスペリエンスと効率が大幅に向上します。これは、FOAKS が線形証明時間の達成に注力している重要な理由でもあります。
一方、暗号学の観点から見ると、ゼロ知識証明システムの設計は証明者と検証者の間の複数ラウンドの対話に依存することがよくあります。たとえば、ゼロ知識証明を紹介する多くの人気科学記事で使用されている「ゼロ知識の洞窟」のストーリーでは、証明の実現は、アリババ (証明者) と記者の間の複数回の情報伝達と対話に依存します (検証者)。しかし実際には、多くのアプリケーション シナリオでは、対話に依存するとシステムが利用できなくなるか、遅延が大幅に増加します。 zkRollup システムと同様に、証明者 (つまり、FOX 内のフォルダー) が、検証者との対話に依存せずに、正しい証明値をローカルで計算できることが期待されます。
最初のレベルのタイトル
ゼロ知識証明への挑戦
ゼロ知識証明アルゴリズムはアプリケーションの普及とともに非常に人気があり、近年ではFOAKS、Orion、zk-starkなどさまざまなアルゴリズムも生まれています。これらのアルゴリズム、および暗号化分野の初期のシグマ プロトコルの核となる証明ロジックは、証明者 (Prover) が最初に特定の値を検証者 (Verifier) に送信し、検証者が次の方法でチャレンジ (Challenge) を生成するというものです。ローカル乱数ランダムに生成されたチャレンジ値が証明者に送信されますが、証明者は検証者を通過する高い確率で応答するための実際の知識を持っている必要があります。例えば、ゼロ知識の洞窟で、記者はコインを投げて、アリババに「左か右から出てください」と言いました。ここでの「左と右」はアリババへの挑戦です。必要な方向に出てください、そうでなければそこに出ます。失敗する確率は半分になります。
ここで、チャレンジの生成が重要なステップであることに気付きます。これには、ランダムで証明者が予測できない 2 つの要件があります。まず、ランダム性はその確率的性質を保証します。 2 番目のポイントは、証明者がチャレンジ値を予測できれば、プロトコルのセキュリティが破られていることを意味します。証明者は知識がなくても検証に合格できます。アナロジーは継続できます。アリババが記者がどちらの側に質問するかを予測できれば、呪文がなくても、事前にその側に入ることができ、結果は合意を通過できることを示しています。
最初のレベルのタイトル
ハッシュ関数
ハッシュ関数の名前は私たちには聞きなれないかもしれませんが、ビットコインのコンセンサスプロトコルPOWにおけるマイニングの数学的問題であっても、データ量の圧縮やメッセージ検証コードの構築などにもハッシュ関数があります。上記のさまざまなプロトコルの中で、ハッシュ関数のさまざまなプロパティが実際に使用されます。
具体的には、安全なハッシュ関数のプロパティには次のようなものがあります。
圧縮性: 決定論的ハッシュ関数は、任意の長さのメッセージを固定長に圧縮できます。
効率: 入力 x が与えられると、出力 h(x) を計算するのは簡単です。
衝突防止: 入力 x 1 が与えられた場合、別の入力 x 2 、 x 1 x 2 、 h(x 1 ) = h(x 2 ) を見つけるのは困難です。
ハッシュ関数が衝突耐性を満たす場合は、一方向性の特性を満たす必要があることに注意してください。つまり、出力 y が与えられた場合、h(x) = y を満たす x を見つけるのは困難です。暗号では、一方向性を絶対に満たす関数を理論的に構築することは不可能ですが、実用上はハッシュ関数は基本的に一方向性関数とみなすことができます。
最初のレベルのタイトル
フィアット シャミール ヒューリスティック (ヒューリスティック)
実際、Fiat-Shamir ヒューリスティック (ヒューリスティック) では、ハッシュ関数を使用して、以前に生成されたスクリプトをハッシュし、チャレンジ値として使用される値を取得します。
画像の説明
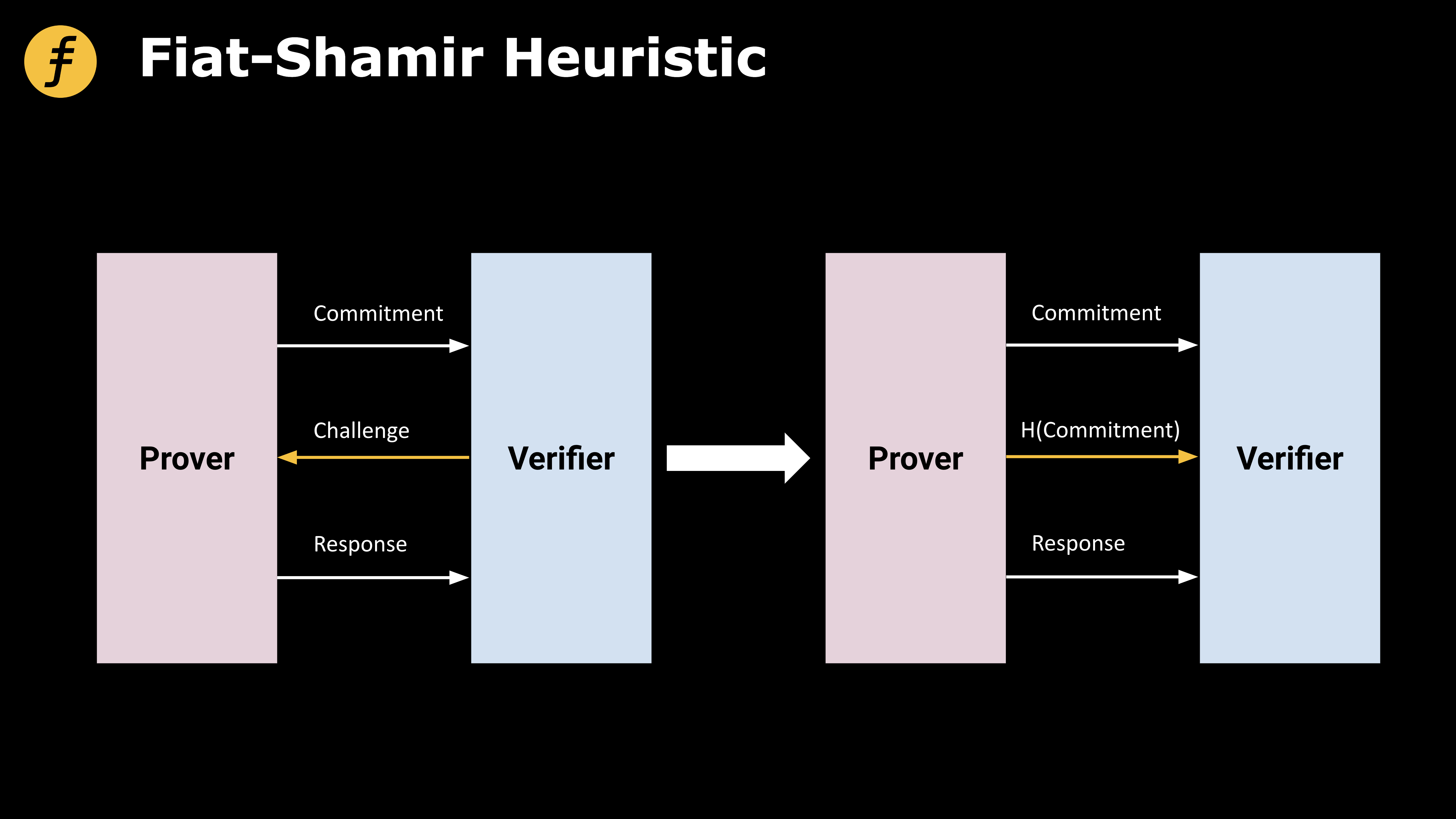
最初のレベルのタイトル
非インタラクティブなFOAK
このセクションでは、FOAKS プロトコルにおける Fiat-Shamir ヒューリスティックの適用を具体的に示します。これは主に、ブレーキダウン部分でチャレンジを生成するために使用され、それによって非対話型 FOAKS を実現します。
画像の説明

図 2: 非インタラクティブプルーフ FOAKS でのブレーキダウンチェック
ここでハッシュ関数を使用し、証明者自身がこのランダム ベクトルを生成できるようにします。
γ0=H(C1、R、r0、r1)とする。これに応じて、検証者の検証計算において、γ0を計算するこのステップも追加する必要がある。この構造によれば、コミットメントが生成される前に、証明者はチャレンジ値を事前に予測できないため、事前にチャレンジ値に応じて対応して「不正」、つまり、対応して偽のコミットメント値を生成することはできないことがわかります。同時に、関数出力のハッシュのランダム性に従って、チャレンジ値もランダム性を満たします。
2 番目の点については、 β =H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 ) とします。
エピローグ
function PC. Commit(ϕ):
Parse was a k × k matrix. The prover locally computes the tensor code encoding C1 ,C2 ,C1 is a k × n matrix,C2 is a n × n matrix.
for i ∈ [n] do
Compute the Merkle tree root Roott=Merkle.Commit(C2 [:, i])
Compute a Merkle tree root R=Merkle.Commit([Root0 ,......Rootn-1 ]), and output R as the commitment.
function PC. Prover(ϕ, X, R)
The prover generates a random vector γ0 ∈ Fk by computing: γ0 =H(C1 , R, r0 , r1 )
Proximity:
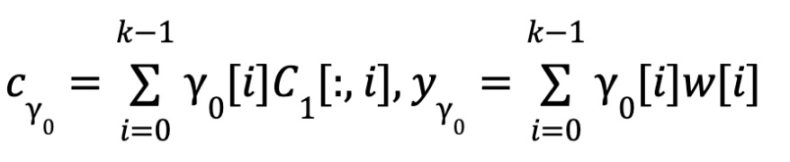
Consistency:
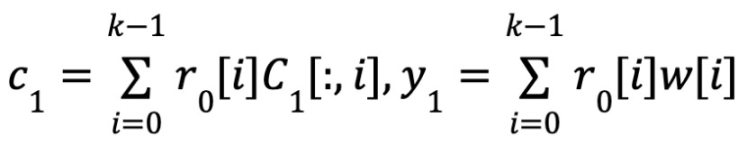
Prover sends c1 , y1 , cγ 0 , yγ 0 to the verifier.
Prover computes a vector Î as challenge, in which Î = H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 )
for idx ∈ Î do
Prover sends C1 [:, idx] and the Merkle tree proof of Rootidx for C2 [:, idx] under R to verifier
function PC. VERIFY_EVAL(ΠX, X, y= ϕ (X), R)
Proximity: ∀idx ∈ Î, Cγ 0 [idx] == <γ0 , C1 [:, idx]> and Ec(yγ 0 ) == Cγ 0
Consistency: ∀idx ∈ Î, C1 [idx] == <γ0 , C1 [:, idx]> and Ec(y1 ) == C1
y==
∀idx ∈ Î, Ec ( C1 [:, idx]) is consistent with ROOTidx, and ROOTidx’s Merkle tree proof is valid.
Output accept if all conditions above holds. Otherwise output reject.
エピローグ
参考文献
参考文献
1.Fiat, Amos; Shamir, Adi ( 1987). "How To Prove Yourself: Practical Solutions to Identification and Signature Problems". Advances in Cryptology — CRYPTO' 86. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 263: 186 – 194. doi: 10.1007/3-540-47721-7 _ 12. ISBN 978-3-540-18047-0.
2.https://www.cnblogs.com/zhuowangy 2 k/p/12246575.html



