Vitalik Buterin: ステルス アドレスに関する不完全なガイド
原作者: ヴィタリック・ブテリン
原文の編集: The Way of DeFi
原作者: ヴィタリック・ブテリン
原文の編集: The Way of DeFi
イーサリアムのエコシステムに残された最大の課題の 1 つはプライバシーです。パブリック ブロックチェーンに送信されるものはすべて、デフォルトでパブリックになります。これはますます、お金や金融取引だけでなく、ENS名、POAP、NFT、魂縛トークンなどを意味します。実際には、イーサリアム アプリケーションのスイート全体を使用すると、生活の重要な部分が公開され、誰でも閲覧および分析できるようになります。
この状況をいかに改善するかが重要な課題となっており、それは広く認識されている。しかし、これまでのところ、プライバシーの向上に関する議論は主に、ETH および主流の ERC 20 トークンのプライバシー保護転送 (多くの場合自己転送) という 1 つの特定の使用例を中心に展開されてきました。この投稿では、他の多くの状況でイーサリアムのプライバシー状態を改善できる別のクラスのツール、つまりステルス アドレスの仕組みと使用例について説明します。
最初のレベルのタイトル
ステルスアドレスシステムとは何ですか?
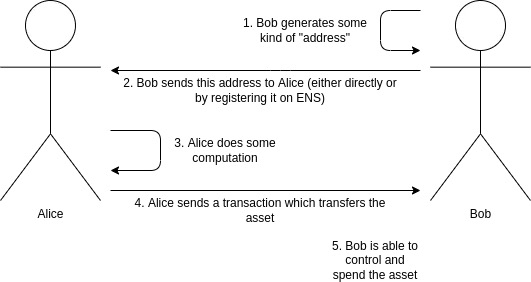
アリスがボブに資産を与えたいと考えているとします。これは、一定量の暗号通貨 (例: 1 ETH、500 RAI)、または NFT である可能性があります。ボブは、アセットを受け取ったときに、それを受け取ったことが世界に知られることを望んでいません。特にオンチェーンにコピーが 1 つだけある NFT の場合、転送が発生したという事実を隠すことは不可能ですが、受信者が誰であるかを隠すことはより現実的である可能性があります。アリスとボブも怠け者です。彼らは、支払いプロセスが現在とまったく同じであるシステムを望んでいます。ボブは、誰かが彼に支払う方法をエンコードしたある種の「アドレス」をアリスに送信します (または ENS に登録します)。アリス (または他の誰か) が彼に資産を送信するには、この情報だけで十分です。
これは、Tornado Cash などのツールによって提供されるプライバシーとは異なることに注意してください。 Tornado Cash は、ETH や主要な ERC 20 トークンなどの主流の代替資産の転送を隠すことができます (ただし、自分にプライベートに送信するのに使用するのが最も簡単です) が、未知の ERC 20 転送にプライバシーを追加するのは非常に弱く、それを行う方法はありません。 NFT転送にプライバシーを追加します。
暗号通貨による支払いの一般的なワークフロー。私たちはプライバシーを高めたいと考えています (アセットを受け取ったのがボブであることを誰も知ることができません) が、ワークフローは同じに保ちたいと考えています。
ステルス アドレスは、そのような解決策を提供します。ステルス アドレスは、アリスまたはボブのいずれかが生成できますが、ボブのみが制御できるアドレスです。ボブは、支出キーを生成して秘密に保ち、そのキーを使用してステルス メタ アドレスを生成します。彼はこのメタアドレスをアリスに渡します (または ENS に登録します)。アリスは、このメタアドレスに対して計算を実行して、ボブに属するステルス アドレスを生成できます。その後、彼女は必要な資産をこのアドレスに送信できるようになり、ボブはそれらの資産を完全に制御できるようになります。転送とともに、彼女は追加の暗号化データ (一時公開キー) をオンチェーンで公開し、ボブがこのアドレスが自分のものであることを発見できるようにします。
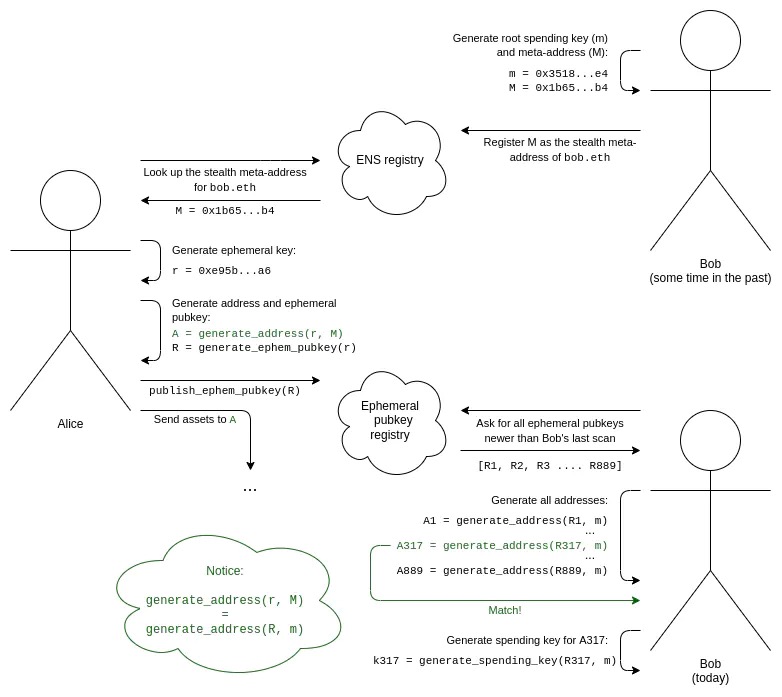
別の方法: ステルス アドレスは、ボブと同じプライバシー プロパティを提供し、トランザクションごとに新しいアドレスを生成しますが、ボブからの対話は必要ありません。
ステルス アドレス スキームの完全なワークフローは次のとおりです。
1. ボブは、ルート支出キー (m) とステルス メタ アドレス (M) を生成します。
2. ボブは、ENS レコードを追加して、M を bob.eth のステルス メタ アドレスとして登録します。
3. アリスがボブが bob.eth であることを知っていると仮定します。アリスは、ENS でステルス メタ アドレス M を検索します。
4. アリスは、自分だけが知っている一時キーを生成し、一度だけ使用します (この特定のステルス アドレスの生成)。
5. アリスは、自分の一時キーとボブのメタ アドレスを組み合わせるアルゴリズムを使用して、ステルス アドレスを生成します。これで、このアドレスに資産を送信できるようになりました。
6. アリスはまた、一時的な公開鍵を生成し、それを一時的な公開鍵レジストリに公開します (これは、資産をステルス アドレスに送信した最初のトランザクションと同じトランザクションで実行できます)。
7. ボブが自分に属するステルス アドレスを発見するには、一時公開キー レジストリをスキャンして、最後のスキャン以降に何らかの理由で誰かが発行した一時公開キーのリスト全体を見つける必要があります。
すべては 2 つのパスワード スプーフィングの使用に依存しています。まず、共有秘密を生成するには 2 つのアルゴリズムが必要です。1 つはアリスの秘密のもの (一時キー) とボブの公開のもの (メタ アドレス) を使用するアルゴリズム、もう 1 つはボブの秘密のもの (ルート支出キー) を使用するアルゴリズムです。 ) とアリスの公開トランザクション (彼女の一時的な公開鍵)。これはさまざまな方法で実行できますが、現代の暗号化の分野を確立した成果の 1 つであるディフィー ヘルマン鍵交換は、まさにそれを実行します。
しかし、共有秘密だけでは十分ではありません。共有秘密から秘密鍵を生成するだけであれば、アリスとボブの両方がこのアドレスから使用できるようになります。そこで停止してボブに資金を新しい住所に転送してもらうこともできますが、それは非効率であり、不必要にセキュリティが低下します。そこで、キーブラインドメカニズムも追加しました。アルゴリズムのペアでは、ボブは共有秘密を自分のルート支出キーと組み合わせることができ、アリスは共有秘密をボブのメタアドレスと組み合わせることができるため、アリスはステルスアドレスを生成でき、ボブはステルス アドレスとボブのメタ アドレスの間 (またはあるステルス アドレスと別のステルス アドレスの間) にパブリック リンクを作成することなく、そのステルス アドレスのキーを消費します。
最初のレベルのタイトル
楕円曲線暗号を使用したステルスアドレス
楕円曲線暗号を使用したステルス アドレスは、2014 年にピーター トッドによってビットコインのコンテキストで初めて導入されました。この手法は次のように機能します (これは、基本的な楕円曲線暗号に関する事前知識があることを前提としています。いくつかのチュートリアルについては、ここ、ここ、およびここを参照してください)。
• ボブは秘密鍵 m を生成し、M = G * m を計算します。ここで、G は相互に合意された楕円曲線の生成点です。目に見えないメタアドレスは M のエンコードです。
• アリスは一時キー r を生成し、一時公開キー R = G * r を公開します。
• アリスは共有秘密 S = M * r を計算でき、ボブは同じ共有秘密 S = m * R を計算できます。
• このアドレスの秘密鍵を計算するために、ボブ (およびボブ単独) は、上記のすべての要件を満たし、非常に簡単な p = m + hash(S) を計算できます。
現在、イーサリアムのステルス アドレス標準を定義しようとする EIP さえあります。これは、このアプローチをサポートし、ユーザーが他のアプローチを開発する余地を残しています (例: ボブが別々の支出とキーの表示を行えるようにする、または量子暗号化を達成するために異なる暗号化を使用できるようにする)。耐性のあるセキュリティ)。ここであなたは次のように考えているかもしれません: ステルス アドレスは難しくない、理論はしっかりしている、採用は単なる実装の詳細です。ただし、問題は、本当に効率的な実装には、かなり大きな実装の詳細を行う必要があることです。
最初のレベルのタイトル
ステルスアドレスと取引手数料の支払い
誰かがあなたにNFTを送ったとします。あなたのプライバシーを考慮して、彼らはあなたが管理するステルスアドレスにそれを送信します。チェーン上のエフェム公開鍵をスキャンした後、ウォレットはこのアドレスを自動的に検出します。この NFT の所有権を自由に証明したり、他の人に譲渡したりできるようになりました。しかし問題がある!アカウントのETHは0なので、取引手数料を支払うことができません。 ERC-4337 トークンの支払い者でさえ、代替可能な ERC 20 トークンでしか機能しないため、機能しません。また、メインウォレットからETHを送信することはできません。公開リンクを作成することになるからです。
この問題を解決する「簡単な」方法があります。ZK-SNARK を使用して資金を送金し、手数料を支払うだけです。しかし、これには大量のガスが消費され、1回の乗り換えに数十万のガスがかかります。
もう 1 つの賢いアプローチには、専門のトランザクション アグリゲーター (MEV 用語では「シーカー」) を信頼することが含まれます。これらのアグリゲーターにより、ユーザーは一度支払うだけで、オンチェーントランザクションの支払いに使用できる一連の「チケット」を購入できるようになります。ユーザーが他に何も含まれていないステルス アドレスで NFT を使用する必要がある場合、ユーザーはショーミアン ブラインディング スキームを使用してエンコードされたチケットの 1 つをアグリゲーターに提供します。これは、1980 年代と 1990 年代に提案された集中型のプライバシー保護電子現金提案で使用された元のプロトコルです。シーカーは「チケット」を受け入れ、トランザクションがブロックで正常に受け入れられるまで、繰り返し無料でトランザクションをバンドルに含めます。関与する資金の量が少なく、取引手数料の支払いにのみ使用できるため、信頼性と規制の問題は、このような集中型のプライバシー保護電子キャッシュの「完全な」実装よりもはるかに低くなります。
最初のレベルのタイトル
ステルス アドレスと個別の支出キーと表示キー
ボブは、すべてを実行するマスター「ルート支出キー」を 1 つだけ持つのではなく、別々のルート支出キーとビュー キーを必要としているとします。キーを見ると、ボブのステルス アドレスをすべて見ることができますが、そこから使用することはできません。
楕円曲線の世界では、これは非常に簡単な暗号トリックを使用して解決できます。
• ボブのメタアドレス M は (K, V) の形式になり、G * k および G * v としてエンコードされます。ここで、k は支出キー、v は表示キーです。
• 共有秘密は S = V * r = v * R になります。ここで、r は依然としてアリスの一時的な鍵であり、R は依然としてアリスの一時的な公開鍵です。
• ステルスアドレスの公開鍵は P = K + G * hash(S)、秘密鍵は p = k + hash(S) です。
最初の賢い暗号化ステップ (共有秘密の生成) では表示キーが使用され、2 番目の賢い暗号化ステップ (ステルス アドレスとその秘密キーを生成するアリスとボブの並列アルゴリズム) ではルート支出キーが使用されることに注意してください。
これには多くの使用例があります。たとえば、ボブが POAP を受信したい場合、ボブは自分の POAP ウォレット (または安全性の低い Web インターフェイス) に表示キーを与えて、インターフェイスに POAP 権限を与えることなく、チェーンをスキャンしてすべての POAP を表示できます。
一時的な公開キーのセット全体をより簡単にスキャンするための 1 つの手法は、各一時的な公開キーにビュー タグを追加することです。上記のメカニズムでこれを行う 1 つの方法は、ビュー ラベルを共有秘密のバイト (たとえば、S モジュロ 256 の x 座標、または hash(S) の最初のバイト) にすることです。
この方法では、ボブは共有秘密を計算するために各一時的な公開キーに対して 1 つの楕円曲線乗算を実行するだけで済み、完全なアドレスを生成して確認するためにボブがより複雑な計算を行うのに必要な時間はわずか 1/256 です。
最初のレベルのタイトル
ステルスアドレスと耐量子セキュリティ
上記のスキームは楕円曲線に依存しており、これは問題ありませんが、残念ながら量子コンピューターに対して脆弱です。量子コンピューターが問題になった場合、量子耐性のあるアルゴリズムに切り替える必要があります。自然な候補としては、楕円曲線ホモロジーと格子の 2 つがあります。
楕円曲線ホモロジーは、楕円曲線に基づく非常に異なる数学的構造であり、上で行ったことと同様の暗号トリックを使用できる線形特性を備えていますが、量子コンピューターの離散対数に対して脆弱になる可能性のある構造をうまく回避しています。 。
ID ベースの暗号化の主な弱点は、その基礎となる数学が非常に複雑であり、この複雑さの中に潜在的な攻撃のリスクがあることです。昨年、同種ベースのプロトコルの一部が侵害されましたが、その他のプロトコルは依然として安全です。ホモロジーの主な利点は、キー サイズが比較的小さいことと、多くの楕円曲線ベースの手法に直接移植できることです。
CSIDH の 3 相同性、出典はこちら。
格子は、楕円曲線同型写像よりもはるかに単純な数学に依存する非常に異なる暗号構造であり、非常に強力な処理 (完全準同型暗号化 (FHE) など) を行うことができます。ステルス アドレス スキームは格子上に構築できますが、最適なスキームを設計することは未解決の問題です。ただし、格子ベースの構造はキー サイズが大きくなる傾向があります。
格子を応用した完全準同型暗号化。 FHE は、別の方法でステルス アドレス プロトコルを支援するために使用することもできます。つまり、ボブがビュー キーを公開せずに、チェーン全体にアセットが含まれているかどうかをチェックするステルス アドレスの計算をアウトソーシングできるようにすることができます。
3 番目のアプローチは、一般的なブラックボックス プリミティブ、つまり多くの人が他の理由で必要とする基本的な要素からステルス アドレス スキームを構築することです。スキームの共有秘密生成部分は、公開キー暗号化システムの重要なコンポーネントであるキー交換に直接マッピングされます。より難しい部分は、アリスに(支出キーではなく)ステルス アドレスのみを生成させ、ボブに支出キーを生成させる並列アルゴリズムです。
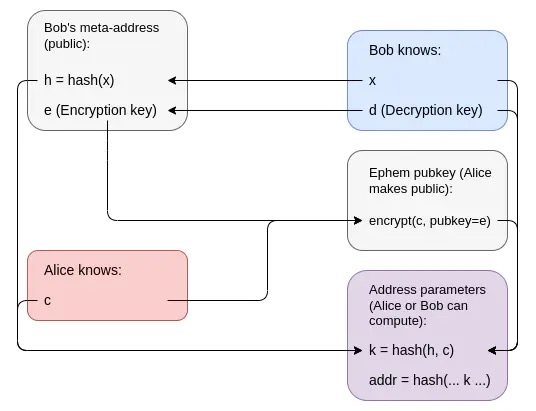
残念ながら、公開鍵暗号システムの構築に必要な要素よりも単純な要素を使用してステルス アドレスを構築することはできません。簡単な証明があります。秘密アドレス スキームを使用して公開キー暗号化システムを構築できるということです。アリスがボブへのメッセージを暗号化したい場合、アリスは N 個のトランザクションを送信できます。各トランザクションはボブのステルス アドレスの 1 つ、またはアリス自身のステルス アドレスの 1 つに送信され、ボブはどのトランザクションを受信してニュースを読むかを確認できます。 。これは重要です。なぜなら、ハッシュだけでは公開キー暗号化を行うことができず、ハッシュだけではゼロ知識証明を行うことができるという数学的証明があるからです。したがって、ステルス アドレスはハッシュだけでは行うことができません。
c の暗号化では、ボブには他の誰についても何も伝えられず、k はハッシュであるため、c についてはほとんど何も明らかにされません。ウォレットコード自体には k のみが含まれており、c はプライベートです。つまり、k から h まで遡ることはできません。
ただし、これには STARK が必要であり、STARK は大きくなります。最終的に、ポスト量子イーサリアムの世界には、多くのスタークを使用する多くのアプリケーションが含まれる可能性が高いと思います。そのため、スペースを節約するために、これらすべてのスタークを 1 つの再帰的スタークに結合する、ここで説明したような集約プロトコルを提唱します。
最初のレベルのタイトル
ステルス アドレス、ソーシャル リカバリ、マルチ L2 ウォレット
私は長い間、ソーシャル リカバリ ウォレットのファンです。これは、キーが機関、他のデバイス、友人の間で共有されるマルチ署名メカニズムを備えたウォレットであり、その一部は圧倒的にアカウントへのアクセスに対して復元できます。マスターキーを紛失した場合。
ただし、ソーシャル リカバリ ウォレットはステルス アドレスとうまく組み合わせられません。アカウントを復元する必要がある場合 (つまり、アカウントを管理する秘密鍵を変更する必要がある場合)、N 個のステルス ウォレットのアカウント検証を変更するいくつかの手順も実行する必要があります。論理的には、これには N 回のトランザクションが必要になりますが、その代わりに高額な手数料、利便性、プライバシーのコストがかかります。
社会的回復と、複数のレイヤー 2 プロトコルの世界の相互作用にも同様の懸念があります。Optimism、Arbitrum、Starknet、Scroll、Polygon のアカウントをお持ちで、おそらくそれらのロールアップの一部には、スケーリング上の理由からインスタンスが 10 ダース並列されている場合、各インスタンスにアカウントがある場合、キーの変更は非常に複雑な操作になる可能性があります。
複数のチェーン内の複数のアカウントのキーを変更するのは膨大な作業です。
これにより、多くのレイヤー 2 プロトコルにまたがる場合でも、多くのアカウントをどこか (ベース チェーンまたはレイヤー 2 上) の単一の値 k によって制御できます。1 つの値を変更するだけですべてのアカウントの所有権を変更できます。アカウント間のリンクを明らかにします。
結論は
最初のレベルのタイトル
結論は



