Paradigm: All DeFi products are perpetual contracts
Original authors: Joe Clark, Andrew Leone, and Dan Robinson, Opyn Research Director, Opyn CEO, and Paradigm Research Director respectively
Original compilation: Luffy, Foresight News
Recently, we have been thinking about power perps. Power perpetual contracts are derivative contracts that track a power of an index, such as an index squared or an index raised to the third power. This is an interesting rabbit hole. The longer you think about power perpetual contracts, the more you’ll realize that everything in the DeFi world is similar to it.
Here, we first throw out three surprising points:
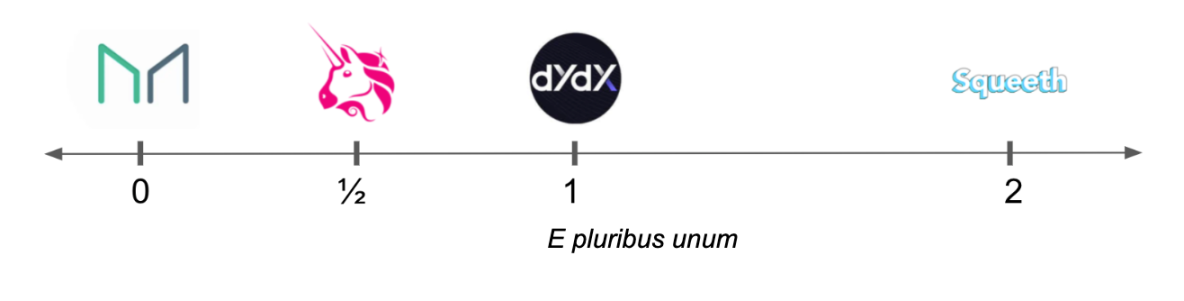
Cryptocurrency-collateralized stablecoins (such as DAI or RAI) are like level 0 perpetual contracts.
Margin futures (such as dYdX) are level 1 perpetual contracts.
Constant product AMMs such as Uniswap are replicating portfolios of 0.5-order perpetual contracts, and constant geometric mean AMMs such as Balancer are replicating portfolios of power perpetual contracts of any value between 0 and 1.
This is cool because it reveals the surprisingly tight design space behind the three main primitives in DeFi. Before explaining one by one, we first need to define perpetual contracts and power perpetual contracts.
Perpetual Contract Definition: An index that tracks an index (note: an index is usually a price, but can be anything measured in numerical form, such as the average temperature in San Francisco or the number of giraffes alive today) and provides unlimited risk exposure. For delivery contracts, the farther the transaction price (mark price) is from the target price (index price), the greater the amount of periodic payment (funding fee).
Graphically, the funding fee payment changes as the gap between the mark price and the index price changes during the funding cycle. If the mark price is higher than the index, longs pay shorts. If the mark price is lower than the index price, shorts pay longs.
There are many mechanisms for paying funding fees (for example, cash or in-kind payments, regular or continuous funding fees, etc.), and there are many mechanisms for setting interest rates based on prices (including the proportional mechanism used by Squeeth and the more complex PID control used by Reflexer device). But all mechanisms are based on the same idea: longs should pay shorts when the mark price is higher than the index price, and vice versa.
Power perpetual contract definition: A perpetual contract that tracks the index price raised to p power.
To create a short position in the Power perpetual contract, you first lock some collateral in a vault and mint (i.e. borrow) the Power perpetual contract. This minted power perpetual contract is sold to enable shorting. If you want to go long, buy from someone who owns a power perpetual contract.
This mechanism is driven by the required collateral to debt ratio:
Collateral Ratio = Equity/Debt = ((Collateral Quantity) * (Collateral Price)) / ((Perpetual Contract Quantity) * (Index Price)^p )
The ratio must remain safely above 1 so that there is enough collateral to cover the debt, otherwise the contract will liquidate the collateral by purchasing enough perpetual contracts to close the position.
Design space of power perpetual contract
The design space of the power perpetual contract involves the power p, the minimum collateral ratio c>1 and three asset choices:
Collateral asset: e.g. USD
Index assets (assets whose value is tokenized): e.g., ETH
Denominated asset (unit of measure of value): Typically USD
We now make three claims.
Claim 1: Stablecoins are zero-order power perpetual contracts
A stablecoin is a loan minted against reliable collateral. The following configuration gives an example of a USD stablecoin:
Collateral assets: ETH
Index asset: ETH
Denominated asset: USD
Mortgage ratio: 1.5
Power: 0
This means we stake ETH and mint stablecoin tokens. The index is the zeroth power of the ETH price, that is, ETH^ 0 = 1.
If I deposit 1 ETH as collateral and ETH is trading at $3000, I can mint up to 2000 tokens.
Collateralization rate = equity/debt = ((collateral quantity) * (collateral price)) / ((power perpetual contract quantity) * (index price)^p)= 1 * 3000/ (2000 * 1) = 1.5
The funding fee is the current trading price (mark price) of the stablecoin minus the index price raised to the power 0.
Funding fee = mark price - index price^ 0 = mark price - 1
The funding fee mechanism provides a good incentive for stablecoin trading prices to be anchored at $1. If it trades well above $1, users sell their stablecoin holdings and then mint and sell more stablecoins for a profit. If the price is trading below $1, users can purchase the stablecoin to earn a positive interest rate and potentially sell it at a higher price in the future.
Not all stablecoins use this precise (mark price - index price) funding fee mechanism, but all collateralized stablecoins share this basic structure, with the stablecoin acting as good collateral for loans. Even stablecoins with interest rates set through governance will set them to a level similar to mark price - 1 to maintain their peg to $1.
Claim 2: Margin futures are power-1 perpetual contracts
If we modify the stablecoin power from the previous section to 1 and change the collateral to USD, we get the tokenized ETH asset:
Collateral assets: USD
Index asset: ETH
Denominated asset: USD
Mortgage ratio: 1.5
Power: 1
I staked $4500 and minted one stable ETH (price $3000).
Collateral ratio = equity/debt = ((collateral quantity) * (collateral price)) / ((power perpetual contract) * (index price) ^p ) = 4500 * 1 / ( 1 * 3000 1) = 1.5
The funding fee for this perpetual contract is the USD trading price (mark price) minus the target index price ^ 1.
Funding fee = mark price - index price ^ 1 = = mark price - ETH/USD price
The funding fee mechanism is a good incentive for perpetual contracts to trade close to the price of ETH. If the price of the perpetual contract increases significantly, the funding fee will encourage arbitrageurs to buy ETH and short the perpetual contract. If the price of the perpetual contract drops significantly, they will be encouraged to sell ETH and buy the perpetual contract.
I could sell this stable ETH asset to short the price of ETH, using USD as collateral.
From tokenized short assets to margined short perpetual assets
The stable ETH asset we built is not very capital efficient. We put up $4,500 in collateral and gained short ETH exposure worth $3,000 (or 1 ETH). We can be more capital efficient by selling minted ETH contract tokens (stableETH) and then using that as collateral to mint more ETH tokens.
If the minimum mortgage rate is 1.5 and ETH is 3000, we operate as follows:
Deposit $4,500 and mint 1 ETH contract token;
Sell ETH contract tokens for $3,000, then use the USD obtained from the sale as collateral to mint 1/1.5 = 0.666 ETH contract tokens;
Sell ETH contract tokens for $2,000 and mint (1/1.5)^2 = 0.444 ETH contract tokens;
Sell ETH contract tokens at $1333.33 and mint (1/1.5)^3 = 0.296 ETH contract tokens.
Note: Leverage can usually be calculated by 1/(collateralization rate-1). In this example, leverage multiple = 1/(1.5-1)= 2.
Ultimately, we minted and sold 3 ETH contract tokens, which was $4,500 in collateral and ended up with $9,000 in short ETH exposure. This position is equivalent to opening a 2x leveraged short ETH/USD perpetual contract.
This process would be simplified if we could use flash transactions or flash loans. We can flash 3 ETH contract tokens into USD and use the proceeds as collateral to mint ETH contract tokens to repay.
If the collateral ratio requirement is 110%, we can open a 10x position.
Go long instead of short
If going long, users can purchase ETH contract tokens. To perform a long leverage operation, users can borrow more USD using ETH contract token collateral and use the borrowed USD to purchase more ETH contract tokens, repeating the process for up to 2x exposure. If using flash transactions or flash loans, this can be done in a single transaction.
This means that overcollateralized perpetual contracts can be converted into undercollateralized perpetual contracts.
Claim 3: Uniswap and other CFMMs are (almost) 0.5 power perpetual contracts
The value of a liquidity position in a Uniswap pool is proportional to the square root of the relative prices of the two assets. For the ETH/USD pool, the value of LP (liquidity provider) is:
V = 2 * (k * (ETH price))^ 0.5
where k is the product of the two token quantities. The trading pool will generate a certain amount of trading fees every cycle.
Now consider the power perpetual contract:
Collateral assets: USD
Index asset: ETH
Denominated asset: USD
Mortgage ratio: 1.2
Power: 0.5
This power perpetual contract will track the square root of the ETH price.
The LP will receive the difference between the funding fee and the AMM fee. Since this trade offsets price risk, the 0.5 power perpetual contract should trade just below:
Expected Uniswap fees = index price - mark price
This gives us a good result for equilibrium Uniswap fees (note: if the trading pair has 90% annualized volatility, you need to get 1/8 * 0.9^2 = 10.125% return from LP fees. So , if you own $100 in Uniswap LP, you need to earn $0.028 per day in fees to cover impermanent losses. The funding fee for a 0.5 power perpetual contract is 2.8 basis points per day.) The funding rate for a 0.5 perpetual contract should be . In the simplified case of zero interest rate:
Equilibrium Uniswap return = σ²/8
where σ² is the variance of the price return of one asset relative to another in the trading pool. We also get this from a Uniswap perspective (see hereAppendix C). we are athereIt is also introduced in detail from the perspective of power.
Therefore, stablecoins (and mortgages more broadly), margined perpetual futures contracts, and AMMs are all a type of power perpetual contract.
What else has been overlooked?
Advanced power perpetual contract: Start with the quadratic power perpetual contract. Squeeth is the first quadratic perpetual contract, providing exposure to quadratic price. By combining high-order power perpetual contracts and 1-order power perpetual contracts with 0-order power perpetual contracts as collateral, we can obtain many approximations of returns.
If we need more precise results, we can simulate any function using a combination of power perpetual contracts with integer powers in Taylor series powers: sin(x), e^x 2, log(x).
What’s next to look forward to? How interesting it would be to have a world that allowed power perpetual contracts, collateralized assets, and Uniswap LP to coexist harmoniously.



