exist"Play and make money"Under the concept, players hope to gain profits while enjoying the game. However, GameFi is limited by high GAS costs and an imperfect blockchain game development ecosystem, and its security and transparency are difficult to be recognized by players. This brings GameFi to the other extreme - constantly optimizing the economic model and revenue, and the revenue cycle continues to shorten, eventually causing a stampede. In the new cycle, the popularity of L2, full-chain game engines and ZK technology will bring users on-chain privacy and more complex on-chain game mechanisms. This simultaneously solves the issues of performance, privacy, and trustworthiness, shifting the focus from Ponzi games to more trustworthy and complex on-chain games. Using application layer ZK technology, game developers can easily build on-chain strategy games with clear requirements for interactive privacy scenarios, and it also brings new hope for more complex trusted (on-chain) game scenarios. Through this article, Salus will explore how the new application layer ZK technology can help games complete scene innovation.

Technical background: The emergence of recursive zkSNARK

zk-SNARK is a cryptographic proof system in which a prover can prove possession of certain information without revealing that information, and without any interaction between the prover and the verifier.

Recursive zkSNARK means that a developer can verify another zkSNARK proof inside a zkSNARK proof and generate a statement of the zkSNARK proof.Recursion allows zkSNARK provers to squeeze more knowledge into their proofs while maintaining simplicity, without significantly slowing down the recursive verification process.

Compared with normal zkSNARK,Recursive zkSNARKs provide enhanced scalability and efficiency by allowing multiple proofs to be compressed into a single proof.This recursive combination reduces the computational load and proof size of complex or multi-step processes, making them particularly beneficial for applications such as blockchain games where a large number of interactions and transactions occur. This will result in higher performance and lower costs for users and developers.

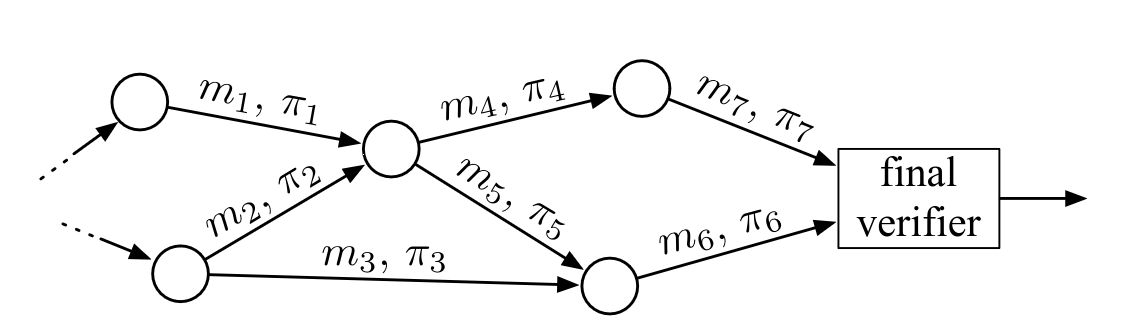
Image Source -https://ethresear.ch/t/signature-merging-for-large-scale-consensus/17386

Recursive SNARKs to unlock new application-level properties

• compression

Recursive zkSNARKs allow provers to put more knowledge into proofs while ensuring that these proofs can still be verified by verifiers in constant or polylogarithmic time. Using recursive zkSNARKs as a rollup of information can independently roll up more computations than the largest (non-recursive) circuit.

• composability

Using recursive zkSNARKs, it is possible to create a chain of proofs where at each step the proof is passed to a new participant, where each participant adds their own knowledge claim without knowing the details of the rest of the chain.

Implementation of recursive SNARK

In general, there are two ways to implement a fully recursive zkSNARK: One way is to use a loop of pairing-friendly elliptic curves, where efficient recursion is achieved by finding two pairing-friendly curves such that the order of one curve is equal to that of the other curve field size; the second approach is to brute force it through and simply implement it in the proof system itselfElliptic Curve Arithmetic on Single Pair of Friendly Curves。

the first method，Cycles of paired friendly elliptic curves, although many researchers are still exploring, it is still difficult to achieve a curve that simultaneously satisfies the two characteristics of pairing friendliness and circulation. The following defines what a pairing-friendly elliptic curve cycle is.

Definition 1:A cycle of elliptic curves is a list of elliptic curves defined over a finite field, where the number of points on one curve is cyclically equal to the size of the domain of the next curve.

The m-cycle of an elliptic curve is composed of m different elliptic curves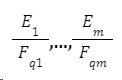,inis a prime number such that the number of points on these curves satisfies the formula: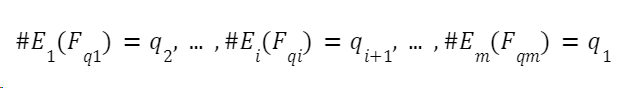

Efficient zkSNARK schemes are generally constructed from pairing-friendly elliptic curves, and the loop conditions in the equation allow them to be combined recursively and avoid expensive modular operations when spanning finite fields with different characteristics.

Definition 2:A pairing-friendly m-cycle of elliptic curves is an m-cycle in which every elliptic curve in the cycle is fundamental and has a small embeddedness.

The second methodis to force through and simply implement elliptic curve arithmetic for a single pair of friendly curves in the proof system itself). You can port the matching circuit toBN 254 curve and then assemble a growth validator in Circom.

Taking the Groth 16 attestation system as an example, Groth 16 has a two-stage trusted setup, with the second stage setup being circuit-specific. This means that when you verify a proof inside a SNARK, it will require a trusted setting independent of the outer SNARK.

Therefore the most suitable applications of recursive groth 16 SNARKs are those that recurse into themselves, i.e. the proofs verified in a circuit are proofs of the same circuit itself. This means we only need a trusted setup. The figure shows the idea of ​​​​self-recursive SNARK:

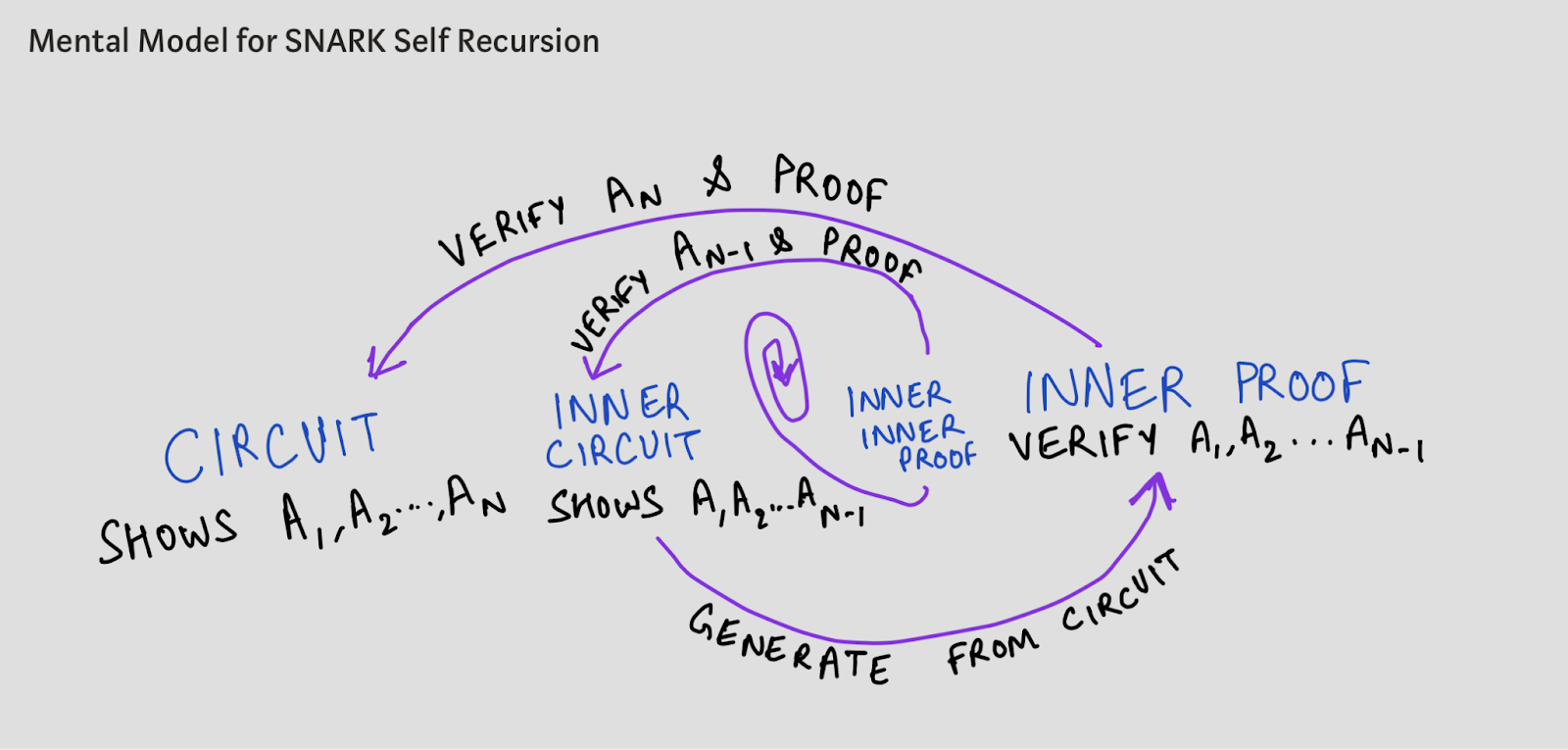
Self-recursive SNARK - Image sourcehttps://0x parc.org/blog/groth 16-recursion

At each step you have a circuit to prove the calculation

the validity of (possibly i is a public input to a SNARK ), and in the ith such proof you verify another proof of computational validityeffectiveness. There are stepsValidity, your SNARK circuit will remain the same on each recursion. byIsokratiaFor example, eachAll are ECDSA signature verification.

In general,Recursive zkSNARKs provide greater scalability: reducing the data and computation required for multi-step games or actions, making them more feasible on-chain, ensuring complex game logic and state transitions are quickly and securely verified.

Case study: ZK-Hunt and its impact

ZK HuntIt is an RTS-like on-chain PvP game that explores the use of ZK technology to achieve complex on-chain game mechanics and information asymmetry. ZK Hunt allows players to perform actions with complete privacy, and each action can be verified without revealing any underlying data.

Movement on the ZK Hunt Plains is public and Player B can see Player As position updates as they move. Entering the jungle is also public, but movement within the jungle is invisible, so player A cannot determine where player B is in the jungle, but can only simulate an ever-growing set of potential locations, shown with question marks. Leaving the jungle and returning to the plains the users location becomes public again, so this potential set of locations disappears.

This information hiding behavior is the basis of ZK Hunt; units have a state (their location) that can change from public to private and back again based on in-game actions. This enhances the strategic nature of the game.

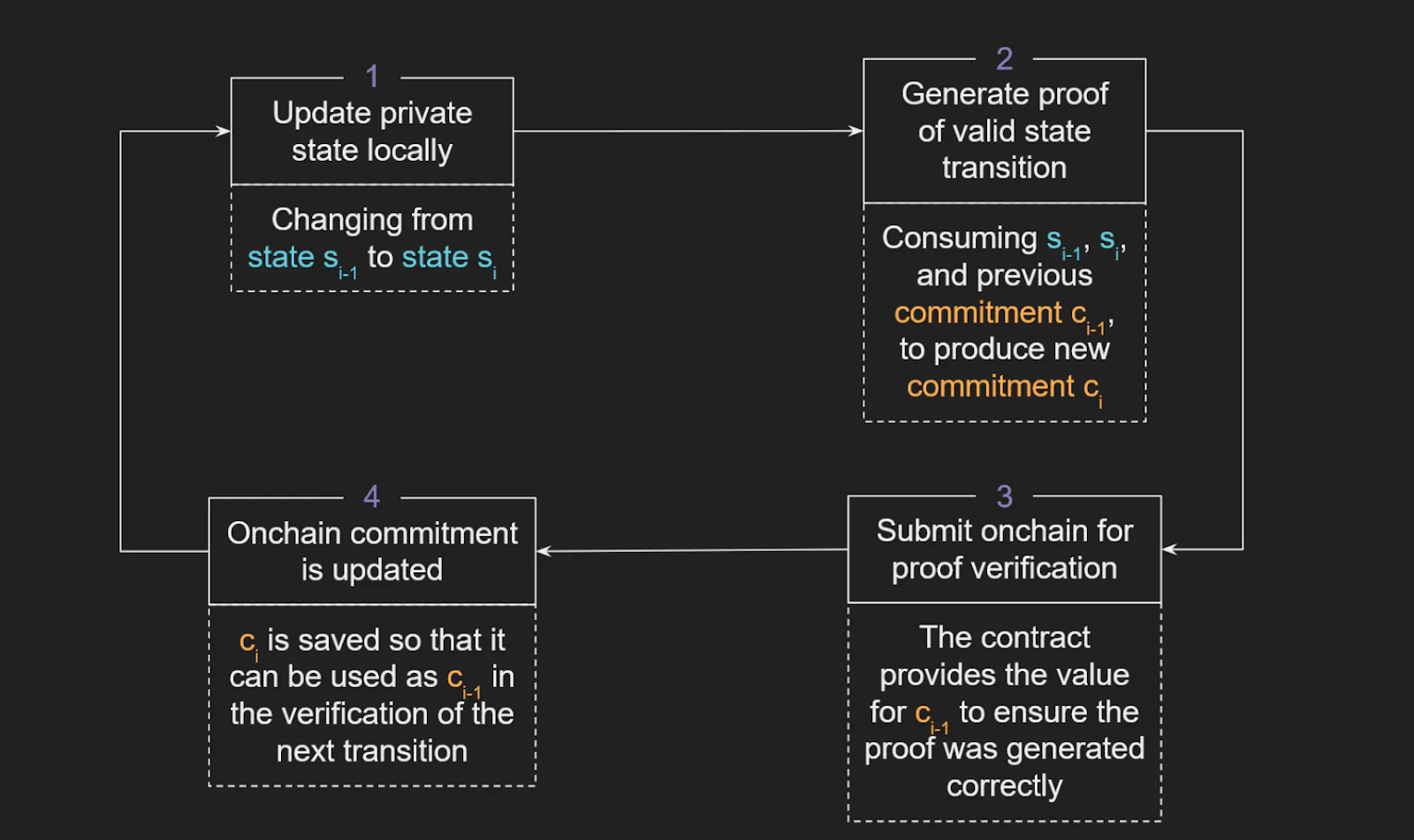
Image Source:https://gam3s.gg/zk-hunt/

As shown in the figure: ZK Hunt’s status verification process mainly consists of the following steps:

1. Update private status locally: from si-1 to si (public to private or private to public)

2. Generate a proof of a valid transition state: consume si-1 and si (and the previous commitment Ci-1, generate a new commitment Ci)

3. Submit to the chain to verify the proof (the contract provides a value for the commitment Ci-1 to ensure that the proof is generated correctly)

4. Update the on-chain commitment (save Ci so it can be used as Ci-1 on the next transition)

promiseis a tool that ZK proofs can use to verify some private state that refers to a users previous commitment without revealing that state to the verifier. The user provides a commitment C as a public input to the proof and a private state s as a private input, and the proof internally computes the commitment that s will produce and checks that it matches C:

Although the cost of ZK proof verification is considered constant (at least for some proof systems, such as Groth 16, etc.), in fact this verification cost increases based on the number of public inputs, which may be important when doing on-chain verification. Meanwhile, ZK Hunt usesposeidon hashAs a commitment scheme, because it is computationally much more efficient within the circuit than other common hash functions, there are fewer constraints per message bit. If the private state is a randomly selected value from a large enough range (such as a private key or a random seed), then simply getting the hash of the value is sufficient as a commitment.

There are many innovative game scenarios that similar ZK technology can achieve, such as asset hiding, decision privacy, and progress confidentiality.

• Asset hiding: In trading card games, players can use zero-knowledge proofs to hide their hand cards and only display necessary information when playing cards.

• Decision privacy: In strategy games, players can secretly choose their next move or allocate resources, with these choices only being made public at specific points or when triggered by game logic.

• Progress secrecy: In an adventure or role-playing game, players may complete quests or gain achievements without others knowing exactly what they have completed, thus maintaining an element of surprise or competitive secrecy.

By using zero-knowledge proof technology, ZK Hunt allows players to conduct game operations while maintaining privacy.This is not only a technological innovation, but also a rule change for on-chain games. In this way, game actions are verified without revealing sensitive data, enhancing the stealth of the strategy and enriching the games strategic depth and element of surprise.

If you are interested in integrating ZK technology into on-chain games to enhance privacy and scalability and achieve game innovation,SalusProvide related services and solutions. By partnering with Salus, you can explore the wide range of applications of ZK technology in gaming, providing players with a richer, safer, and more strategic gaming experience.