TinyRam instruction set and circuit constraints
Introduction
first level title
Introduction
Tinyram is a simple RISC random-access machine with byte-addressable random-access memory and input tapes. There are two variants of TinyRAM: one following the Harvard architecture and one following the von Neumann architecture (in this article we mainly discuss the von Neumann architecture).
The Concise Computational Integrity and Privacy Research (SCIPR) project built mechanisms to prove the correct execution of TinyRAM programs, and TinyRAM was designed to be efficient in this case. It strikes a balance between the opposites of "expressive enough" and "simple enough":
• Sufficient expressiveness to support short and efficient assembly code when compiled from a high-level programming language.Introduction to TinyRam
Introduction to TinyRam
first level title
Tinyram instruction set
Tinyram has a total of 29 instructions, and each instruction consists of an opcode and up to three operands. An operand can be the name of a register (an integer between 0 and K-1), or an immediate value (string of W bits). Unless otherwise specified, instructions do not modify flags individually. Each instruction increases pc by i (i % 2^W) by default, for vnTinyram i= 2W/8.

In general, the first operand is the target register for the instruction calculation, the other operands specify the parameters required by the instruction, and finally, all instructions require one cycle of the machine to execute.
bit manipulation

Integer operations
• shlThese are various unsigned and signed integer operations. In each case, flag is set to 1 if an arithmetic overflow or error (such as division by zero) occurs, and to 0 otherwise.
• shrshift operation
The instruction shl ri rj A stores the W-bit string obtained by left-shifting [rj] by [A]u bit into the ri register. Empty positions after shifting are filled with 0s. Additionally flag is set to the most significant bit of [rj].
The instruction shr ri rj A stores the W-bit string obtained by right-shifting [rj] by [A]u bits in the ri register. Empty positions after shifting are filled with 0s. Also flag is set to the least significant bit of [rj].

comparison operation
• movEach of the instructions in the comparison operation does not modify any registers; the result of the comparison is stored in flag.
• cmovmove operation
The instruction mov ri A stores [A] into the ri register.
Instruction cmov ri A If flag = 1, store [A] into the ri register. Otherwise the value of the ri register will not be changed.
• jmpJump operation
• cjmpThese jump and conditional jump instructions do not modify registers and flags but modify pc.
• cnjmp The instruction jmp A stores [A] into pc.
The instruction cjmp A stores [A] in pc under the condition of flag = 1, otherwise pc is incremented by 1.
The instruction cnjmp A stores [A] in pc under the condition of flag = 0, otherwise pc is incremented by 1.

Memory operation
These are simple memory load and store operations, where the address of memory is determined by an immediate value or the contents of a register. These are the only addressing modes in tinyram. (tinyram does not support the common "base+offset" addressing mode).

input operation
output operation

This instruction indicates that the program has finished computing, so no further operations are allowed.
first level title

instruction set constraints
Tinyram uses the R1CS constraint form for circuit constraints, the specific form is as follows:
An R1CS constraint can have three linear_combination representations of a, b, and c. The assignment of all variables in an R1CS system can be divided into two parts: primary input and auxiliary input. Primary is what we often call "statement". auxiliary is "witness".
An R1CS constraint system contains multiple R1CS constraints. The vector length of each constraint is fixed (primary input size + auxiliary input size + 1).
• andTinyram uses a lot of custom gadgtes in the code implementation of libsnark to express the constraints of vm and the constraints of opcode execution and memory. The specific code is in the gadgetslib1/gadgets/cpu_checkers/tinyram folder.

bit manipulation constraints
Constraint formula:

The R1CS constraint of and verifies parameter 1 and parameter 2 and the calculation result bit by bit for multiplication calculation. The constraint steps are as follows:
1. Calculation process constraints, the code is as follows:

2. Result encoding constraints

• or3. The calculation result is not all 0 constraints (keep consistent with the definition of the instruction, this process is mainly to prepare for the constraint flag)

4.flag constraints
Constraint formula:

The specific constraint steps are as follows:
1. Calculation process constraints, the code is as follows:
2. Result coding constraints (same as above)
• xor3. The calculation result is not all 0 constraints (keep consistent with the definition of the instruction, this process is mainly to prepare for the constraint flag) (same as above)

4.flag constraints (same as above)
Constraint formula:
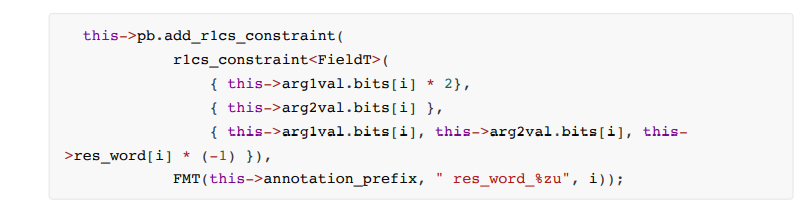
The specific constraint steps are as follows:
•not1. Calculation process constraints, the code is as follows:

Step 2, 3, 4 same as above

Constraint formula:
The specific constraint steps are as follows:
•addStep 2, 3, 4 same as above

Integer Manipulation Constraints
: Constraint formula:
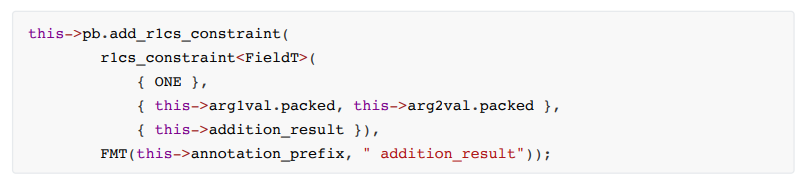
The specific constraint steps are as follows:
1. Calculation process constraints, the code is as follows:
•sub2. Decoding result constraints and boolean constraints
3. Coding result constraints

: Constraint formula:
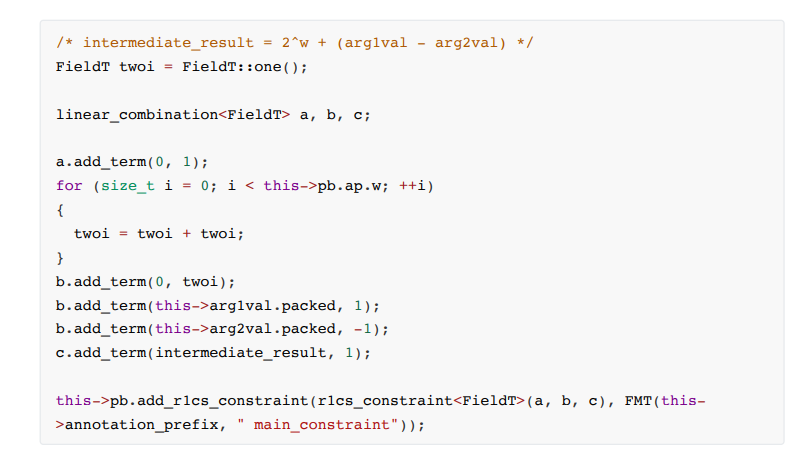
The sub constraint is a little more complicated than add. An intermediate variable is used to represent the result of a - b. At the same time, 2^w is added to the result to ensure that the result calculation is expressed in the form of positive integers and symbols. The specific constraint steps are as follows:
1. Calculation Process Constraints
•mull 、umulh、smulh2. Decoding result constraints and boolean constraints

3. Sign bit constraints
Constraint formula:
Mull-related constraints involve the following steps
1. Calculate the multiplicative constraints
•udiv 、umod2. Calculation result coding constraints

Constraint formula:

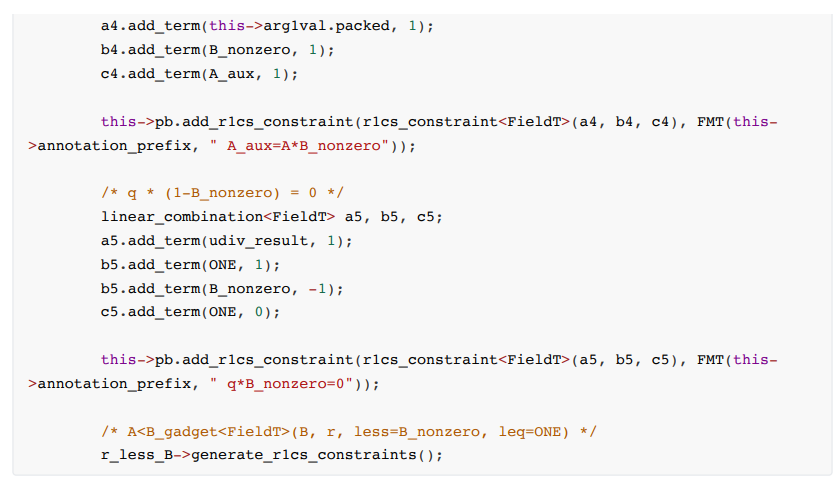
B is the divisor, q is the quotient, and r is the remainder. The remainder sum needs to meet the condition that it cannot exceed the divisor. The specific constraint code is as follows:
• shl、shrsecondary title
shift operation constraint
constraint formulacmpe、 cmpa 、cmpae、cmpg、cmpgecomparison operation
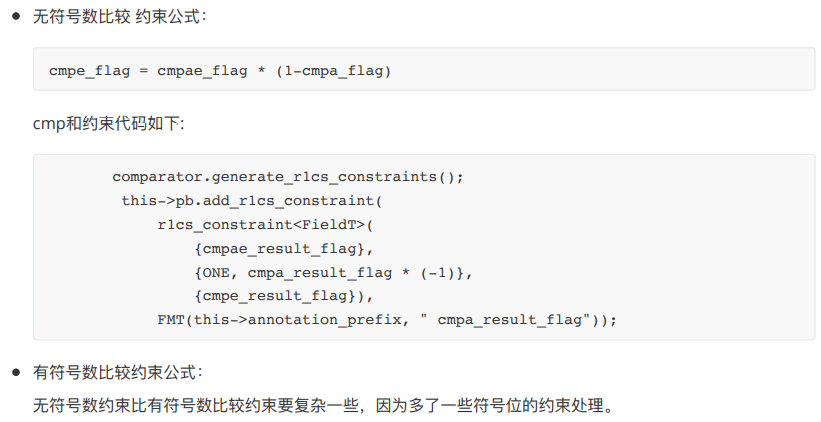
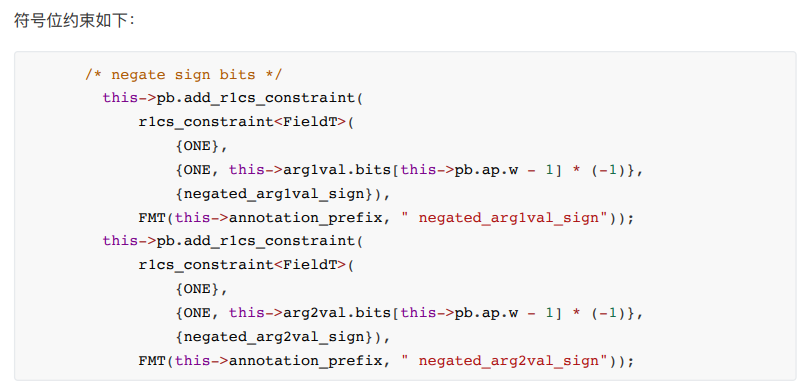
. The comparison instructions can be divided into two categories, namely the comparison of signed numbers and the comparison of unsigned numbers. The core of the constraint process of both uses the comparison_gadget implemented in libsnark.
The rest of the procedure is the same as for signed comparison constraints
• movsecondary title
move operation constraints

• cmovConstraint formula:

Constraint formula:
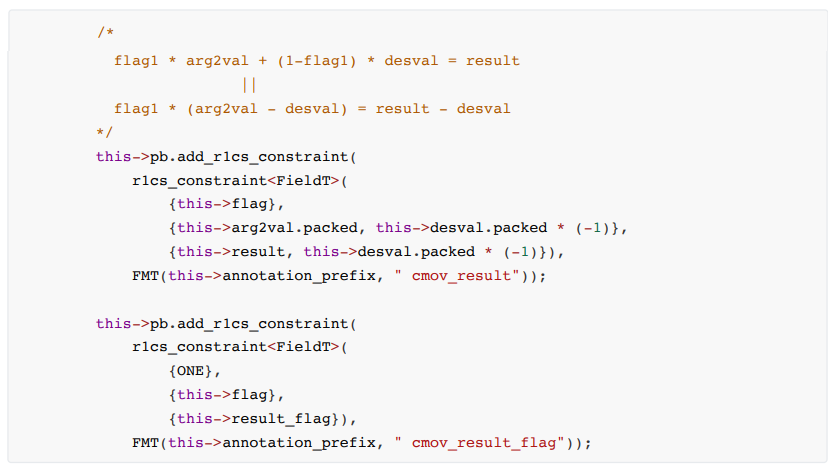
The constraints of cmov are more complicated than those of mov. The main behavior of mov is related to the change of flag value. At the same time, cmov will not modify the flag, so the constraint needs to ensure that the value of flag does not change. The code of cmov is as follows:
secondary title
• jmp
Jump operation constraints

• cjmp
These jump and conditional jump instructions do not modify registers and flags but modify pc.
The Jmp operation constrains the pc value to be consistent with the instruction execution result. The specific constraint code is as follows:

cjmp jumps according to the flag condition, flag = 1 to jump, otherwise pc is incremented by 1

• cnjmp
The constraint formula is as follows:
The constraint code is as follows:

cnjmp jumps according to the flag condition, flag = 0 to jump, otherwise pc is incremented by 1

The constraint formula is as follows:
Memory operation constraints
• store.b and store.w
These are simple memory load and store operations, where the address of memory is determined by an immediate value or the contents of a register. These are the only addressing modes in tinyram. (tinyram does not support the common "base+offset" addressing mode).

and
For store.w, the value of the entire arg1val is taken, and for store.b, the opcode will only take the necessary part of arg1val (for example: the last byte). The constraint code is as follows:

• load.b and load.w
• read
For these two instructions, the content we require to be loaded from memory is stored in instruction_results. The constraint code is as follows:
Input Operational Constraints
The read operation is related to tape, and the specific constraint rules are:
1. The content in the previous tape has been read, there is no content to read, and the next tape will not be read.
2. The content in the previous tape has been read, there is no content to read, and the flag is set to 1
3. If the currently executed instruction is read, then the content read by read is consistent with the input content of tape
5. The result is not 0, which means the flag is 0

Constraint code:
secondary title
• answer
Output Operation Constraints
When the output value of the program is accepted, has_accepted will be set to 1, and the return value of the program can be accepted normally means that the current instruction is answner and arg2 value is 0.

other
The constraint code is as follows:

From the example in the above figure, it can be concluded that it is impossible to verify all EVM operations using vnTinyram + zk-SNARKs, and it is only suitable for verifying the calculation verification of a small number of instructions. You can use vnTinyram to verify the opcode of some calculation types of EVM.
about Us
first level title
about Us
GitHub | Twitter | Telegram | Medium| Mirror | HackMD | HackerNoon



