LUCIDA:如何利用多因子策略构建强大的加密资产投资组合(因子合成篇)
書接上回,關於《用多因子模型建立強大的加密資產投資組合》系列文章中,我們已經發布了三篇:《理論基礎篇》、《資料預處理篇》、《因子有效性檢驗篇》。
前三篇分別解釋了多因子策略的理論與單因子測試的步驟。
一、因子相關性檢定的原因:多重共線性
我們透過單因子測試部分篩選出一批有效因子,但以上因子不能直接入庫。因子本身可依具體的經濟意義進行大類劃分,同類型的因子間存在較強的相關性,若不經相關性篩選直接入庫,根據不同因子進行多元線性回歸求預期回報率時,會出現多重共線性問題。在計量經濟學中,多重共線性是指回歸模型中的一些或全部解釋變數存在「完全」或準確的線性關係(各變數間高度相關)。
因此,有效因子篩選出後,首先需要根據大類對因子的相關性進行T 檢驗,對於相關性較高的因子,要麼捨棄顯著性較低的因子,要麼進行因子合成。
多重共線性的數學解釋如下:
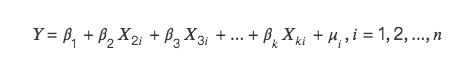
會有兩種情況:

多重共線性所導致的後果:
1.完全共線性下參數估計量不存在
2.近似共線性下OLS 估計量非有效


3.參數估計量經濟意義不合理
4.變數的顯著性檢驗(t 檢驗)失去意義
5.模型的預測功能失效:透過多元線性模型擬合的預測報酬率極不準確,模型失效。
二、步驟一:同類型因子的相關性檢驗
檢驗新求出的因子與已入庫因子的相關性。通常來說,有兩類資料求相關性:
1.根據所有token 在回測期間的因子值求相關
2.根據所有token 在回測期間的因子超額報酬值求相關

我們所求的每一個因子對token 的報酬率都有一定的貢獻和解釋能力。進行相關性檢定**,是為了找出對策略效益有不同解釋和貢獻的因子,策略的最終目的是效益**。如果兩個因子對收益的刻畫是相同的,即使兩個因子值存在很大差異也無意義。因此,我們並不是想找出因子值本身差異大的因子,而是想找出因子對收益刻畫不同的因子,所以最終選擇了以因子超額報酬值求相關。
我們的策略是日頻,所以以回測區間的日期計算因子超額報酬之間的相關係數矩陣

程式求解與庫內相關最高的前n 個因子:
def get_n_max_corr(self, factors, n= 1):
factors_excess = self.get_excess_returns(factors)
save_factor_excess = self.get_excess_return(self.factor_value, self.start_date, self.end_date)
if len(factors_excess) < 1:
return factor_excess, 1.0, None
factors_excess[self.factor_name] = factor_excess['excess_return']
factors_excess = pd.concat(factors_excess, axis= 1)
factors_excess.columns = factors_excess.columns.levels[ 0 ]
# get corr matrix
factor_corr = factors_excess.corr()
factor_corr_df = factor_corr.abs().loc[self.factor_name]
max_corr_score = factor_corr_df.sort_values(ascending=False).iloc[ 1:].head(n)
return save_factor_excess, factor_corr_df, max_corr_score
三、步驟二:因子取捨、因子合成
對於相關性較高的因子集合,可以採取兩種方式處理:
(1)因子取捨
根據因子本身的ICIR 值、收益率、換手率、Sharpe 比率,挑選某維度下最有效的因子來保留,刪除其他因子。
(2)因子合成
將因子集合中的因子進行合成,截面上盡可能多的保留有效訊息

假設目前有3 個待處理的因子矩陣:

2.1 等權加權
各因子權重相等(w= 1/因子個數),綜合因子=各因子值加總求平均。
Eg.動量類因子,一個月收益率、兩個月收益率、三個月收益率、六個月收益率、十二個月收益率,這六個因子的因子負荷各佔1/6 的權重,合成新的動量因子負荷,然後再重新進行標準化處理。
synthesis 1 = synthesis.mean(axis= 1) # 依行求平均值
2.2 歷史IC 加權、歷史ICIR、歷史利益加權
以回測期的IC 值(ICIR 值、歷史收益值)對因子進行加權。過去有很多期,每一期都有一個IC 值,所以用它們的平均值作為因子的權重。通常使用回測期IC 的平均值(算數平均值)作為權重。

2.3 歷史IC 半衰加權、歷史ICIR 半衰加權
2.1 與2.2 都是計算算數平均值,回測期的每一次IC、ICIR 對於因子的作用被預設為相同。
但現實中,回測期的每一期對於當期的影響程度不完全相同,存在時間上的衰減。越接近當期的時期,影響越大,越遠影響越小。在此原理,求IC 權重前先定義一個半衰權重,距離當期越近的權重值越大、越遠權重越小。
半衰權重數學推導:


2.4 最大化ICIR 加權
通過求解方程,計算最優因子權重w 使得ICIR 最大化

協方差矩陣的估計問題:協方差矩陣用於衡量不同資產之間的關聯性。統計學中常以樣本協方差矩陣取代總體協方差矩陣,但在樣本數不足時,樣本協方差矩陣與總體協方差矩陣的差異會很大。所以有人提出了壓縮估計的方法,原理是使估計協方差矩陣與實際協方差矩陣之間的均方誤差最小
方式:
1.樣本協方差矩陣

2.Ledoit-Wolf 收縮:引入一個縮小係數,將原始的協方差矩陣與單位矩陣進行混合,以減少雜訊的影響。

3.Oracle 近似收縮:對Ledoit-Wolf 收縮的改進,目標是透過對協方差矩陣進行調整,從而在樣本大小較小的情況下更準確地估計真實的協方差矩陣。 (程式實現與Ledoit-Wolf 收縮同理)
2.5 主成分分析PCA
主成分分析(Principal Component Analysis,PCA)是一種用於降維和提取數據主要特徵的統計方法。其目標是透過線性變換,將原始資料映射到一個新的坐標系,使得數據在新坐標系下的變異數最大化。
具體而言,PCA 首先找到資料中的主成分,也就是資料中變異數最大的方向。然後,它找到與第一個主成分正交(無關)且具有最大變異數的第二個主成分。這個過程一直重複,直到找到資料中所有的主成分。




