LUCIDA:如何利用多因子策略构建强大的加密资产投资组合(因子有效性检验篇)
前言
書接上回,關於《用多因子模型建立強大的加密資產投資組合》系列文章中,我們已經發布了兩篇:《理論基礎篇》、《資料預處理篇》
本篇是第三篇:因子有效性檢定。
在求出具體的因子值後,需要先對因子進行有效性檢驗,篩選符合顯著性、穩定性、單調性、收益率要求的因子;因子有效性檢驗通過分析本期因子值與預期收益率的關係,從而確定因子的有效性。主要有3 種經典方法:
IC / IR 法:IC / IR 值為因子值與預期收益率的相關係數,越大因子表現越好。
T 值(回歸法):T 值反映下期回報率對本期因子值線性回歸後係數的顯著性,透過比較此回歸係數是否透過t 檢驗,來判斷本期因子值對下期回報率的貢獻程度,通常用於多元(即多因子)回歸模型。
分層回測法:分層回測法是基於因子值對token 分層,再計算每層token 的報酬率,進而判斷因子的單調性
一、IC / IR 法
(1)IC / IR 的定義
IC:即資訊係數Information Coefficient,代表因子預測Tokens 收益的能力。某一期IC 值為本期因子值及下期報酬率的相關係數。
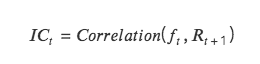

IC 越接近1 ,表示因子值和下期收益率的正相關性越強,IC= 1 ,表示該因子選幣100% 準確,對應的是排名分最高的token,選出來的token 在下個調倉週期中,漲幅最大;
IC 越接近-1 ,表示因子值和下期收益率的負相關性越強,如果IC=-1 ,則代表排名分最高的token,在下個調倉週期中,跌幅最大,是一個完全反指的指標;
若IC 越接近0 ,則表示該因子的預測能力極為弱,表示該因子對於token 沒有任何的預測能力。
IR:資訊比information ratio,代表因子取得穩定Alpha 的能力。 IR 為所有期IC 平均值除以所有期IC 標準差。
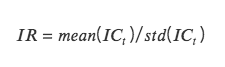
當IC 的絕對值大於0.05 (0.02) 時,因子的選股能力較強。當IR 大於0.5 時,因子穩定取得超額收益能力較強。
(2)IC 的計算方式
Normal IC (Pearson correlation):計算皮爾森相關係數,最經典的一種相關係數。但此計算方式有較多假設前提:資料連續,正態分佈,兩個變數滿足線性關係等等。
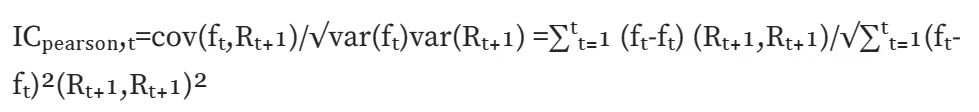
Rank IC (Spearmans rank coefficient of correlation):計算斯皮爾曼秩相關係數,先將兩個變數排序,再依照排序後的結果求皮爾森相關係數。斯皮爾曼秩相關係數評估的是兩個變量之間的單調關係,並且由於轉換為排序值,因此受數據異常值影響較小;而皮爾森相關係數評估的是兩個變數之間的線性關係,不僅對原始資料有一定的前提條件,而且受資料異常值影響較大。在現實計算中,求rank IC 更符合。
(3)IC / IR 法代碼實現
建立一個按日期時間升序排列的唯一日期時間值的清單--記錄調倉日期def choosedate(dateList, cycle)
class TestAlpha(object):
def __init__(self, ini_data):
self.ini_data = ini_data
def chooseDate(self, cycle, start_date, end_date):
'''
cycle: day, month, quarter, year
df: 原始資料框df,date 列的處理
'''
chooseDate = []
dateList = sorted(self.ini_data[self.ini_data['date'].between(start_date, end_date)]['date'].drop_duplicates().values)
dateList = pd.to_datetime(dateList)
for i in range(len(dateList)-1):
if getattr(dateList[i], cycle) != getattr(dateList[i + 1 ], cycle):
chooseDate.append(dateList[i])
chooseDate.append(dateList[-1 ])
chooseDate = [date.strftime('%Y-%m-%d') for date in chooseDate]
return chooseDate
def ICIR(self, chooseDate, factor):
# 1.先展示每個調倉日期的IC,即ICt
testIC = pd.DataFrame(index=chooseDate, columns=['normalIC','rankIC'])
dfFactor = self.ini_data[self.ini_data['date'].isin(chooseDate)][['date','name','price', factor]]
for i in range(len(chooseDate)-1):
# ( 1) normalIC
X = dfFactor[dfFactor['date'] == chooseDate[i]][['date','name','price', factor]].rename(columns={'price':'close 0'})
Y = pd.merge(X, dfFactor[dfFactor['date'] == chooseDate[i+ 1 ]][['date','name','price']], on=['name']).rename(columns={'price':'close 1'})
Y['returnM'] = (Y['close 1'] - Y['close 0']) / Y['close 0']
Yt = np.array(Y['returnM'])
Xt = np.array(Y[factor])
Y_mean = Y['returnM'].mean()
X_mean = Y[factor].mean()
num = np.sum((Xt-X_mean)*(Yt-Y_mean))
den = np.sqrt(np.sum((Xt-X_mean)** 2)*np.sum((Yt-Y_mean)** 2))
normalIC = num / den # pearson correlation
# ( 2) rankIC
Yr = Y['returnM'].rank()
Xr = Y[factor].rank()
rankIC = Yr.corr(Xr)
testIC.iloc[i] = normalIC, rankIC
testIC =testIC[:-1 ]
# 2.基於ICt,求[IC_Mean, IC_Std,IR,IC<0 佔比--因子方向,-IC->0.05 比例]
'''
ICmean: |IC|>0.05,因子的選幣能力較強,因子值與下期收益率相關性高。 -IC-<0.05,因子的選幣能力較弱,因子值與下期收益率相關性低
IR: |IR|>0.5,因子選幣能力較強, IC 值較穩定。 -IR-<0.5,IR 值偏小,因子較不有效。若接近0,基本上無效
IClZero(IC less than Zero): IC<0 佔比接近一半->因子中性.IC>0 超過一大半,為負向因子,即因子值增加,收益率降低
ICALzpF(IC abs large than zero poin five): |IC|>0.05 比例偏高,表示因子大部分有效
'''
IR = testIC.mean()/testIC.std()
IClZero = testIC[testIC<0 ].count()/testIC.count()
ICALzpF = testIC[abs(testIC)>0.05 ].count()/testIC.count()
combined =pd.concat([testIC.mean(), testIC.std(), IR, IClZero, ICALzpF], axis= 1)
combined.columns = ['ICmean','ICstd','IR','IClZero','ICALzpF']
# 3.IC 調倉期內IC 的累積圖
print("Test IC Table:")
print(testIC)
print("Result:")
print('normal Skewness:', combined['normalIC'].skew(),'rank Skewness:', combined['rankIC'].skew())
print('normal Skewness:', combined['normalIC'].kurt(),'rank Skewness:', combined['rankIC'].kurt())
return combined, testIC.cumsum().plot()
二、T 值檢驗(回歸法)
T 值法同樣檢驗本期因子值與下期回報率關係,但與ICIR 法分析二者的相關性不同,t 值法將下期回報率作為因變量Y,本期因子值作為自變量X,由Y對X 回歸,將回歸出因子值的回歸係數進行t 檢驗,檢驗其是否顯著異於0 ,即本期因子是否影響下期報酬率。
此方法本質是雙變量回歸模型的求解,具體公式如下:
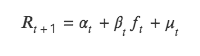

(1)回歸法理論

(2)回歸法代碼實現
def regT(self, chooseDate, factor, return_ 24 h):
testT = pd.DataFrame(index=chooseDate, columns=['coef','T'])
for i in range(len(chooseDate)-1):
X = self.ini_data[self.ini_data['date'] == chooseDate[i]][factor].values
Y = self.ini_data[self.ini_data['date'] == chooseDate[i+ 1 ]][return_ 24 h].values
b, intc = np.polyfit(X, Y,1) # 斜率
ut = Y - (b * X + intc)
# 求t 值t = (\hat{b} - b) / se(b)
n = len(X)
dof = n - 2 # 自由度
std_b = np.sqrt(np.sum(ut** 2) / dof)
t_stat = b / std_b
testT.iloc[i] = b, t_stat
testT = testT[:-1 ]
testT_mean = testT['T'].abs().mean()
testT L1 96 = len(testT[testT['T'].abs() > 1.96 ]) / len(testT)
print('testT_mean:', testT_mean)
print(T 值大於1.96 的佔比:, testT L1 96)
return testT
三、分層回測法
分層指對所有token 分層,回測指計算每層token 組合的報酬率。
(1)分層
首先取得token 池對應的因子值,透過因子值對token 進行排序。升序排序,即因子值較小的排在前面,依排序對token 進行等分。第0 層token 的因子值最小,第9 層token 的因子值最大。
理論上「等分」是指均等分拆token 的個數,即每層token 個數相同,並藉助分位數實現。現實中token 總數不一定是層數的倍數,即每層token 個數不一定相等。
(2)回測
將token 依因子值升序分完10 組後,開始計算每組token 組合的報酬率。此步驟將每層的token 當成一個投資組合(不同回測期,每層的token 組合所含的token 都會有變化),併計算該組合整體的下期回報率。 ICIR、t 值分析的是當期因子值和下期整體的回報率,但分層回測需要計算回測時間內每個交易日的分層組合報酬率。由於有許多回測期有很多期,在每一期都需要進行分層和回測。最後將每一層的token 收益率進行累乘,計算出token 組合的累積報酬率。
理想狀態下,一個好的因子,第9 組的曲線報酬率最高,第0 組的曲線報酬率最低。
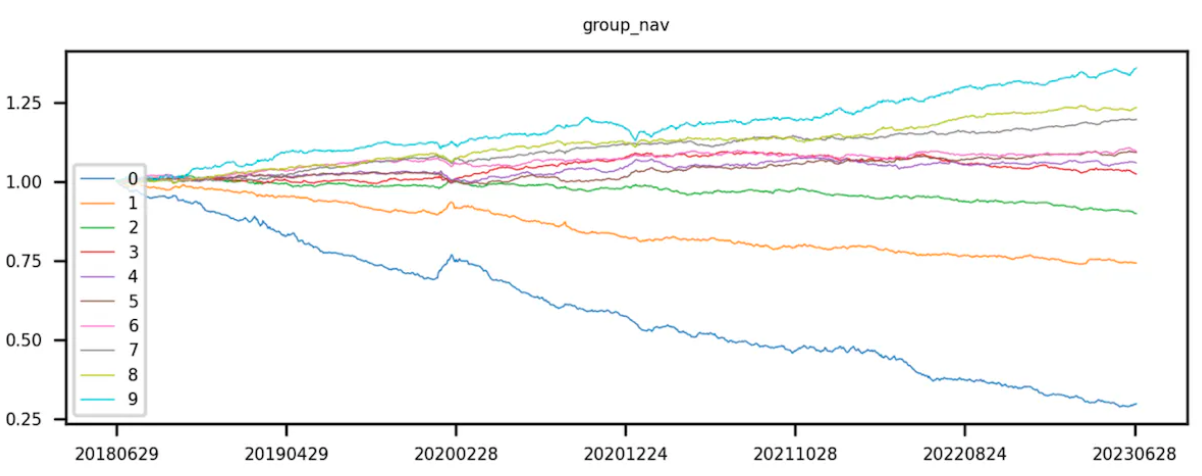
第9 組減去第0 組(即多空收益)曲線呈現單調遞增。
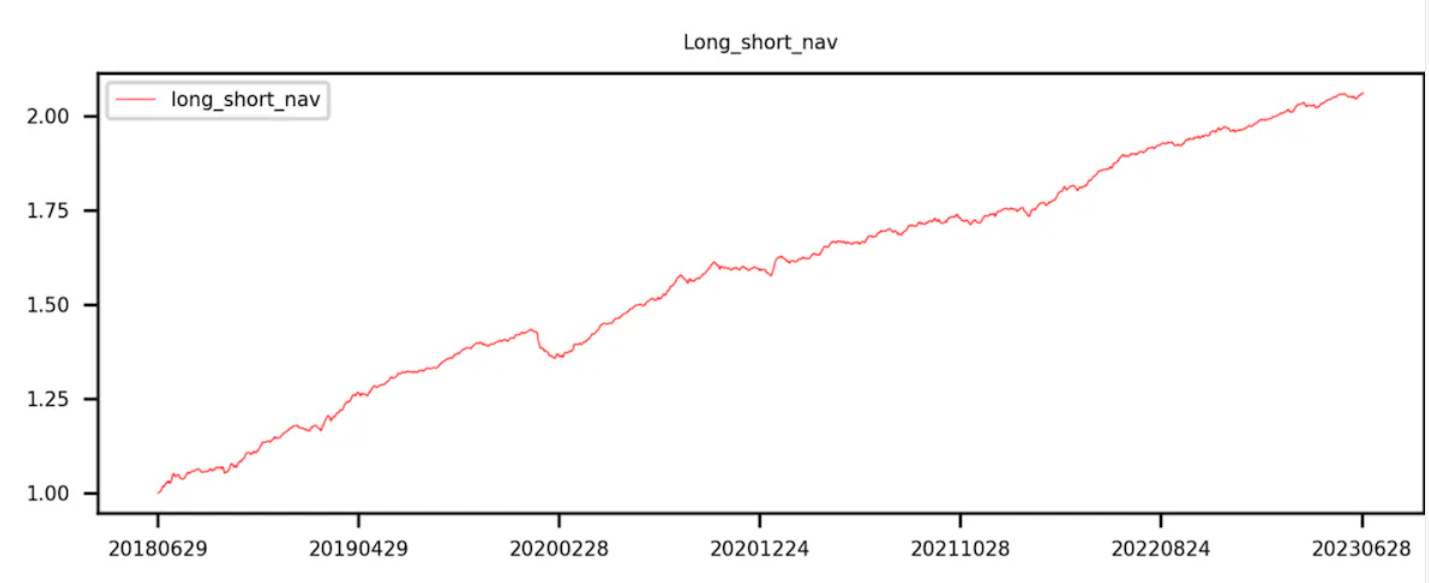
(3)分層回測法代碼實現
def layBackTest(self, chooseDate, factor):
f = {}
returnM = {}
for i in range(len(chooseDate)-1):
df 1 = self.ini_data[self.ini_data['date'] == chooseDate[i]].rename(columns={'price':'close 0'})
Y = pd.merge(df 1, self.ini_data[self.ini_data['date'] == chooseDate[i+ 1 ]][['date','name','price']], left_on=['name'], right_on=['name']).rename(columns={'price':'close 1'})
f[i] = Y[factor]
returnM[i] = Y['close 1'] / Y['close 0'] -1
labels = ['0','1','2','3','4','5','6','7','8','9']
res = pd.DataFrame(index=['0','1','2','3','4','5','6','7','8','9','LongShort'])
res[chooseDate[ 0 ]] = 1
for i in range(len(chooseDate)-1):
dfM = pd.DataFrame({'factor':f[i],'returnM':returnM[i]})
dfM['group'] = pd.qcut(dfM['factor'], 10, labels=labels)
dfGM = dfM.groupby('group').mean()[['returnM']]
dfGM.loc[LongShort] = dfGM.loc[0]- dfGM.loc[9]res[chooseDate[i+ 1 ]] = res[chooseDate[ 0 ]] * ( 1 + dfGM[returnM ]) data = pd.DataFrame ({分層累積報酬率:res.iloc[: 10,-1 ],Group:[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ]})
df 3 = data.corr()
print("Correlation Matrix:")
print(df 3)
return res.T.plot(title='Group backtest net worth curve')



