Curve穩定幣設計白皮書（中英文參照版本）

一級標題Curve Finance

原文編譯：JamesX，iZUMi Research

Overview

The design of the stablecoin has few concepts: lending-liquidating amm algorithm (LLAMMA), PegKeeper, Monetary Policy are the most important ones. But the main idea is in LLAMMA: replacing liquidations with a special-purpose AMM.

圖片描述

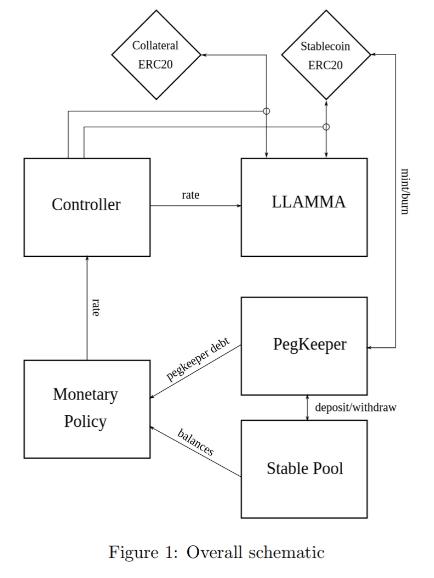
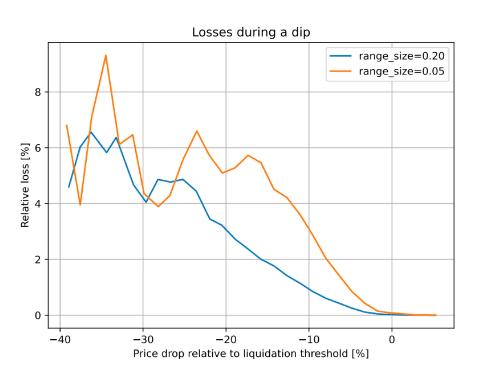
Figure 2 : Dependence of the loss on the price shift relative to the liquidation threshold. Time window for the observation is 3 days

正文

In this design, if someone borrows against collateral, even at liquidation threshold, and the price of collateral dips and bounces - no significant loss happen. For example, according to simulations using historic data for ETH/USD since Sep 2017 , if one leaves the CDP unattended for 3 days and during this time the price drop of 10% below the liquidation threshold happened - only 1% of collateral gets lost.

二級標題

AMM for continuous liquidation/deliquidation (LLAMMA)

一級標題

The core idea of the stablecoin design is Lending-Liquidating AMM Algorithm. The idea is that it converts between collateral (for example, ETH) and the stablecoin (let’s call it USD here). If the price of collateral is high - a user has deposits all in ETH, but as it goes lower, it converts to USD. This is very different from traditional AMM designs where one has USD on top and ETH on the bottom instead.

原文編譯：

The below description doesn’t serve as fully self-consistent rigorous proofs. A lot of that (especially the invariant) are obtained from dimensional considerations. More research might be required to have a full mathematical description, however the below is believed to be enough to implement in practice.

一級標題

This is only possible with an external price oracle. In a nutshell, if one makes a typical AMM (for example with a bonding curve being a piece of hyperbola) and ramps its “center price” from (for example) down to up, the tokens will adiabatically convert from (for example) USD to ETH while proving liquidity in both ways on the way (Fig. 3 ). It is somewhat similar to avoided crossing (also called Landau-Zener transition) in quantum physics (though only as an idea: mathematical description of the process could be very different). The range where the liquidity is concentrated is called band here, at the constant po band has liquidity from pcd to pcu. We seek for pcd(po) and pcu(po) being functions of po only, functions being more steep than linear and, hence, growing faster than po(Fig. 4 ). In addition, let’s defifine prices p↓and p↑ being prices where p↓(po) = po, and p↑(po) = po, defining ends of bands in adiabatic limit (e.g. p = po).

圖片描述"圖片描述"正文

圖片描述

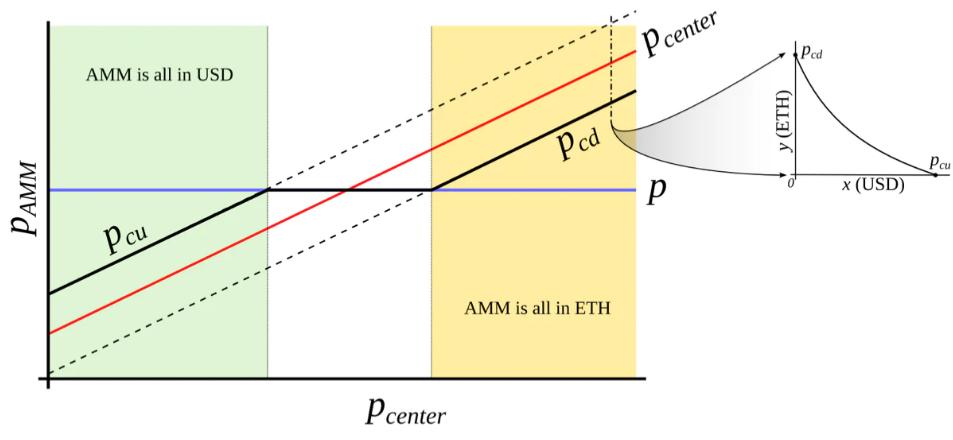Figure 3 : Behavior of an “AMM with an external price source”. External price pcenter determines a price around which liquidity is formed. AMM supports liquidity concentrated from prices pcd to pcu, pcd < pcenter < pcu. When current price p is out of range between pcd and pcu, AMM is either fully in stablecoin (when at pcu) or fully in collateral (when at pcd). When pcd ≤ p ≤ pcu, AMM price is equal to the current price p.

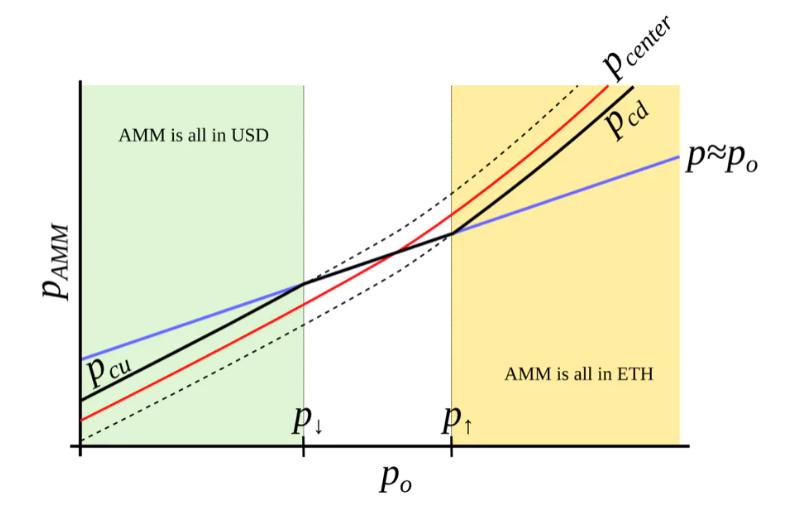Figure 4 : AMM which we search for. We seek to construct an AMM where pcd and pcu are such functions of po that when po grows, they grow even faster. In this case, this AMM will be all in ETH when ETH is expensive, and all in USD when ETH is cheap.

We start from a number of bands where, similarly to Uniswap 3 , hyperbolic shape of the bonding curve is preserved by adding virtual balances. Let say, the amount of USD is x, and the amount of ETH is y, therefore the “amplifified” constant-product invariant would be:

二級標題"一級標題"二級標題

We also can denote x 0 ≡ x  +  f and y 0 ≡ y + g so that the invariant can be written as a familiar I =  x 0 y 0. However, f and g do not stay constant: they change with the external price oracle (and so does the invariant I, so it is only the invariant while the oracle price po is unchanged). At a given po, f and g are constant across the band. As mentioned before, we denote p↑ as the top price of the band and p↓as the bottom price of the band. We defifine A (a measure of concentration of liquidity) in such a way that:

持續清算/無需清算的AMM（LLAMMA）

The property we are looking for is such that higher price po should lead to even higher price at the same balances, so that the current market price (which will, on average, follow po) is lower than that, and the band will trade towards being all in ETH (and the opposite is also true for the other direction). It is possible to find many ways to satisfy that but we need one:

穩定幣設計的核心思想是Lending-Liquidating AMM算法。這個想法是，它在抵押品（例如ETH）和穩定幣（這裡姑且稱之為USD）之間進行轉換。如果抵押品的價格很高--用戶的存款都是ETH，但當價格降低時，它就會轉換為USD穩定幣。這與傳統的AMM設計有很大不同，傳統的AMM設計是將USD穩定幣放在上面（AMM曲線上半截），ETH放在下面（AMM曲線下半截）。

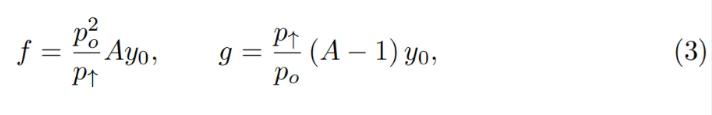
where y 0 is a p 0 -dependent measure of deposits in the current band, denominated in ETH, defifined in such a way that when current price p, p↑ and po are equal to each other, then y = y 0 and x = 0 (see the point at po = p↑ on Fig. 4 ). Then if we substitute y at that moment:

下面的描述並不能作為一個完全自洽的嚴謹證明。很多東西（尤其是不變量）都是從各種維度考慮得到的。要有一個完整的數學描述，可能需要更多的研究，然而下面的描述被認為足以支持在智能合約中實施。

Price is equal to dx 0 /dy 0 which then for a constant-product invariant is:

這只有通過外部預言機餵價才能實現。簡而言之，如果一個人做了一個典型的AMM（例如，粘合曲線是一塊雙曲線），並將其

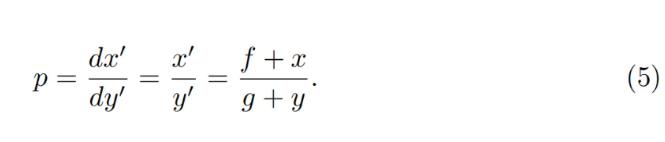
One can substitute situations where po = p↑ or po = p↓ with x = 0 or y = 0 correspndingly to verify that the above formulas are self-consistent.

中心價格

Typically for a band, we know p↑ and, hence, p↓, po, constant A, and also x and y (current deposits in the band). To calculate everything, we need to find yo. It can be found by solving the quadratic equation for the invariant:

從（例如）下降到上升，代幣將從（例如）USD“絕熱”地轉換為ETH，同時在過程中提供兩種方式的流動性（圖3 ）。這有點類似於量子物理學中的“迴避交叉”（也稱為Landau-Zener躍遷）（雖然只是一個概念：對該過程的數學描述可能非常不同）。

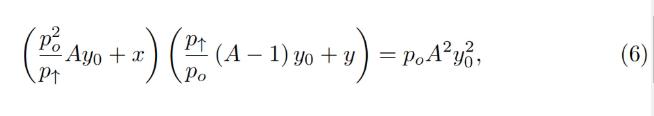
which turns into the quadratic equation against yo:

圖片描述

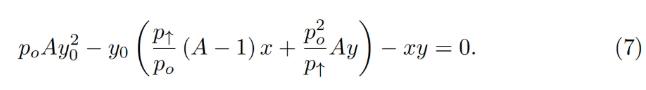
In the smart contract, we solve this quadratic equation in get_y 0 function.

圖片描述

While oracle price po stays constant, the AMM works in a normal way, e.g. sells ETH when going up / buys ETH when going down. By simply substituting x = 0 for the “current down” price pcd or y = 0 for the “current up” price pcu values into the equation of the invariant respectively, it is possible to show that AMM prices at the current value of po and the current value of p↑ are:

我們從一些波段開始，與Uniswap 3 類似，通過增加“虛擬餘額”，保留了粘合曲線的雙曲形狀。比方說，USD的數量是x，ETH的數量是y，因此"增強的"常數-產品不變性將是："我們也可以表示x 0 ≡x+f和y 0 ≡y+g，這樣不變式就可以寫成熟悉的I=x 0 y 0 。然而，f和g並不是保持不變的：它們隨著外部預言機價格的變化而變化（不變量I也是如此，所以它只是在預言機價格po不變時的不變量）。在給定的po下，f和g在整個波段內是不變的。如前所述，我們把p↑表示為波段的頂部價格，p↓表示為波段的底部價格。我們對A（衡量流動性集中度的指標）的定義是這樣的："我們正在尋找的屬性是這樣的：更高的價格po應該導致在相同的餘額下更高的價格，因此，當前的市場價格（平均來說，將跟隨po）低於這個價格，並且波段將朝著全部為ETH的方向交易（而另一個方向也是如此）。可以找到很多方法來滿足，但我們需要這樣一個：

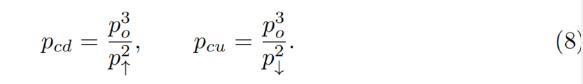
Another practically important question is: if price changes up or down so slowly that the oracle price po is fully capable to follow it adiabatically, what amount y↑ of ETH (if the price goes up) or x↓ of USD (if the price goes down) will the band end up with, given current values x and y and that we start also at p = po. While it’s not an immediately trivial mathematical problem to solve, numeric computations showed a pretty simple answer:

其中y 0 是一個與p 0 相關的衡量當前波段存款的指標，以ETH為單位，其定義是：噹噹前價格p、p↑和po相互相等時，則y=y 0 ，x= 0 （見圖4 上po=p↑的點）。那麼，如果我們把那一刻的y替換掉：

We will use these results when evaluating safety of the loan as well as the potential losses of the AMM.

價格等於dx 0 /dy 0 ，那麼對於一個恆定的產品不變量來說，就是：

Now we have a description of one band. We split all the price space into bands which touch each other with prices p↓ and p↑ so that if we set a base price pbase and have a band number n:

我們可以用x= 0 或y= 0 來代替po=p↑或po=p↓的情況，以驗證上述公式是自洽的。

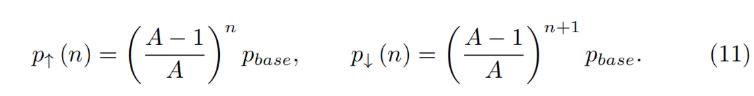
It is possible to prove that the solution of Eq. 7 and Eq. 5 for any band gives:

通常對於一個波段，我們知道p↑，因此也知道p↓、po、常數A，還有x和y（波段中的當前存款）。為了計算剩下的一切，我們需要找到yo。它可以通過解決不變量的二次方程來找到：

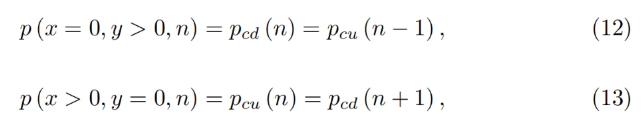
which shows that there are no gaps between the bands.

在預言機價格po保持不變的情況下，AMM以正常的方式工作，例如，上漲時賣出ETH/下跌時買入ETH。通過簡單地將x= 0 替換為

Trades occur while preserving the invariant from Eq. 1 , however the current price inside the AMM shifts when the price po: it goes up when po goes down and vice versa cubically, as can be seen from Eq. 8.

一級標題

LLAMMA vs Stablecoin

Stablecoin is a CDP where one borrows stablecoin against a volatile collateral (cryptocurrency, for example, against ETH). The collateral is loaded into LLAMMA in such a price range (such bands) that if price of collateral goes down relatively slowly, the ETH gets converted into enough stablecoin to cover closing the CDP (which can happen via a self-liquidation, or via an external liquidation if the coverage is too close to dangerous limits, or not close at all while waiting for the price bounce).

當前下跌

When a user deposits collateral and borrows a stablecoin, the LLAMMA smart contract calculates the bands where to locate the collateral.  When the price of the collateral changes, it starts getting converted to the stablecoin. When the system is “underwater”, user already has enough USD to cover the loan. The amount of stablecoins which can be obtained can be calculated using a public get_x_down method. If it gives values too close to the liquidation thresholds - an external liquidator can be involved (typically shouldn’t happen within a few days or even weeks after the collateral price went down and sideways, or even will not happen ever if collateral price never goes up or goes back up relatively quickly). A health method returns a ratio of get_x_down to debt plus the value increase in collateral when the price is well above “liquidation”.

的價格pcd或y= 0 替換為"當前上漲"另一個重要的實際問題是：如果價格的變化如此緩慢，以至於預言機價格po完全能夠”絕熱地”（在一個波段內）跟隨它，那麼在給定當前值x和y，並且我們也從p=po開始的情況下，這個波段最終會得到多少y↑的ETH（如果價格上漲）或x↓的USD（如果價格下跌）。雖然這不是一個立即可以解決的數學問題，但數字計算顯示了一個相當簡單的答案："清算"在評估借貸的安全性以及AMM的潛在損失時，我們將使用這些結果。

When a stablecoin charges interest, this should be reflected in the AMM, too. This is done by adjusting all the grid of prices. So, when a stablecoin charges interest rate r, all the grid of prices in the AMM shifts upwards with the same rate r which is done via a base_price multiplier. So, the multiplier goes up over time as long as the charged rate is positive.

現在我們有了對一個波段的描述。我們把所有的價格空間分成若干波段，這些波段的價格p↓和p↑相互接觸，因此，如果我們設定一個基礎價格pbase，並有一個波段號n：

When we calculate get_x_down or get_y_up, we are first looking for the amounts of stablecoin and collateral x∗ and y∗ if current price moves to the current price po. Then we look at how much stablecoin or collateral we get if po adiabatically changes to either the lowest price of the lowest band, or the highest price of the highest band respectively. This way, we can get a measure of how much stablecoin we will which is not dependent on the current instantaneous price, which is important for sandwich attack resistance.

對於任何一個波段，可以證明公式7 和公式5 的解都可以得到：
**

It is important to point out that the LLAMMA uses po defined as ETH/USD price as a price source, and our stablecoin could be traded under the peg (ps < 1 ) or over peg (ps > 1 ). If ps < 1 , then price in the LLAMMA is p > po.

這表明波段之間沒有空隙。

In adiabatic approximation, p = po/ps, and all the collateral<>stablecoin conversion would happen at a higher oracle price / as if oracle price was lower and equal to:

一級標題<>一級標題

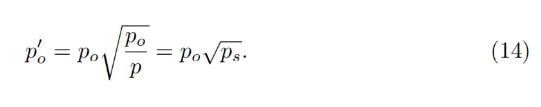
At this price, the amount of stablecoins obtained at conversion is higher by factor of 1/ps (if ps < 1 ) .

清算<1 ）。

It is less desirable to have ps > 1 for prolonged times, and for that we will use the stabilizer (see next)

自動穩定器和貨幣政策

Automatic Stabilizer and Monetary Policy

自動穩定器和貨幣政策

When ps > 1 (for example, because of the increased demand for stablecoin), there is peg-keeping reserve formed by an asymmetric deposit into a stableswap Curve pool between the stablecoin and a redeemable reference coin or LP token. Once ps > 1 , the PegKeeper contract is allowed to mint uncollateralized stablecoin and (only!) deposit it to the stableswap pool single-sided in such a way that the final price after this is still no less than 1. When ps < 1 , the PegKeeper is allowed to withdraw (asymmetrically) and burn the stablecoin.

時，一個健康的方法會返回get_x_down與債務的比率，再加上抵押品的價值增加。

These actions cause price ps to quickly depreciate when it’s higher than 1 and appreciate if lower than 1 because asymmetric deposits and withdrawals change the price. Even though the mint is uncollateralized, the stablecoin appears to be implicitly collateralized by liquidity in the stablecoin pool. The whole mint/burn cycle appears, at the end, to be profitable while providing stability.

當一個穩定幣收取利息時，這應該反映在AMM中。也要反映出來。這是通過調整價格的所有網格來實現的。因此，當一個穩定幣收取利率r時，AMM中的所有價格格都會向上移動，與相同的利率r，這是通過一個基礎價格乘數完成的。所以，只要收取的利率是正的,乘數會隨著時間的推移而上升。

Let’s denote the amount of stablecoin minted to the stabilizer (debt) as dst and the function which calculates necessary amount of redeemable USD to buy the stablecoin in a stableswap AMM get_dx as fdx(). Then, in order to keep reserves not very large, we use the “slow” mechanism of stabilization via varying the borrow r:

當我們計算get_x_down或get_y_up時，我們首先要找的是如果當前價格移動到當前價格po的穩定幣和抵押品x∗和y∗的數量。然後我們看一下，如果po絕熱地變化到最低區間的最低價格，或最高區間的最高價格，我們分別得到多少穩定幣或抵押品。這樣，我們就可以得到一個衡量我們將獲得多少穩定幣的標準，它不依賴於當前的瞬時價格，這對夾層攻擊的阻力很重要。 **"需要指出的是，LLAMMA使用定義為ETH/USD價格的po作為價格來源，我們的穩定幣可以在掛鉤之下（ps<1 ）或超過掛鉤（ps>1 ）進行交易。如果ps<1 ，那麼LLAMMA中的價格就是p>po。"在這個價格下，轉換時獲得的穩定幣的數量要高出1/ps的係數（如果ps

where h is the change in ps at which the rate r changes by factor of 2 (higher ps leads to lower r). The amount of stabilizer debt dst will equilibrate at different value depending on the rate at ps = 1 r 0. Therefore, we can (instead of setting manually) be reducing r 0 while dst/supply is larger than some target number (for example, 5%) (thereby incentivizing borrowers to borrow-and-dump the stablecoin, decreasing its price and forcing the system to burn the dst) or increasing if it’s lower (thereby incentivizing borrowers to return loans and pushing ps up, forcing the system to increase the debt dst and the stabilizer deposits).

一級標題

自動穩定器和貨幣政策

The presented mechanisms can, hopefully, solve the riskiness of liquidations for stablecoin-making and borrowing purposes. In addition, stabilizer and automatic monetary policy mechanisms can help with peg-keeping without the need of keeping overly big PSMs.

一級標題