原文作者：Vitalik Buterin

原文作者：

• 原文作者：

• 原文作者：

• 當前的數據可用性抽樣（DA 抽樣或DAS）計劃使用KZG commitments（KZG 承諾）完成。 KZG 承諾的優點是它們非常易於使用，並且具有一些非常好的代數性質：

• 一個評估證明具有恆定的大小，並且可以在恆定的時間內進行驗證。

這裡存在一種算法來計算所有證明，這些證明在O(N∗log(N)) 時間內在N 個單位根的每一個都會評估deg

您可以線性組合承諾以獲得這個線性組合的承諾：com(P)+com(Q)=com(P+Q)

• 您可以線性組合證明：Proof(P,x)+Proof(Q,x)+Proof(P+Q,x)

• 第一點是良好的效率保證。第二點確保生成可以進行DA 採樣的blob 很容易：如果生成所有證明需要O(N2) 這麼長的時間，則需要高度中心化的參與者或複雜的分佈式算法才能使其準備好DAS。

第三點和第四點對於2D 採樣非常有價值，並且可以實現分佈式區塊生產者和高效的自我修復：區塊生產者只需要知道原始的M 承諾即可使用一種按照曲線的FFT（FFT-over-the-curve） 來“擴展列”並生成在同一deg

您不僅可以進行每行重建，還可以進行每列重建：如果列上的某些值和證明丟失（但仍有一半以上可用），您可以執行FFT 來恢復丟失的值和證明。

如果我們不想支付KZG 的成本，我們可以使用內積參數（IPA）來代替嗎？

• IPA 具有以下特性：

• 有關IPA 的解釋，請參閱這篇文章的前半部分。

• IPA 具有以下特性：

• 評估證明具有對數大小，可以在線性時間內驗證（一個大小為4096 的多項式大約需要40 毫秒）

沒有已知的有效的多重證明生成算法。

承諾是橢圓曲線點，您可以像KZG 承諾一樣將它們線性組合

沒有已知的線性組合證明的方法。

因此，我們保留了一些屬性，也丟失了一些屬性。事實上，我們失去的足夠多，以至於我們生成、分發和自我修復證明的“當前方法”不再可能。這篇文章描述了一種替代方法，雖然有點笨拙，但仍然可以實現目標。

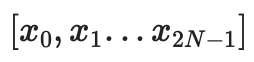
一種替代方法

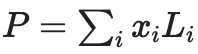
首先，我們生成一棵證明樹，而不是為deg

我們以評估形式解釋數據，將其視為一個向量：

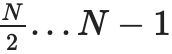
，其中多項式

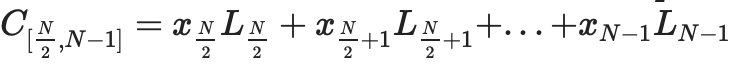
（其中Li 是在坐標i 和0 處等於1 的deg<2N 多項式在集合中的其他坐標）。

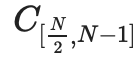
證明樹中的每個節點都是對該部分數據的承諾，以及該承諾實際上“在界限內”的證明。例如，

節點將包含承諾

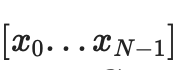
。將有一個IPA 證明，

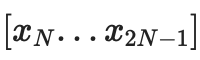
實際上是這些點的線性組合，沒有其他點。
我們生成兩棵樹，第一棵用於

，第二棵用於

，對一條數據的“完整”承諾由C[0,N− 1] 和C[N,2N-1]組成。

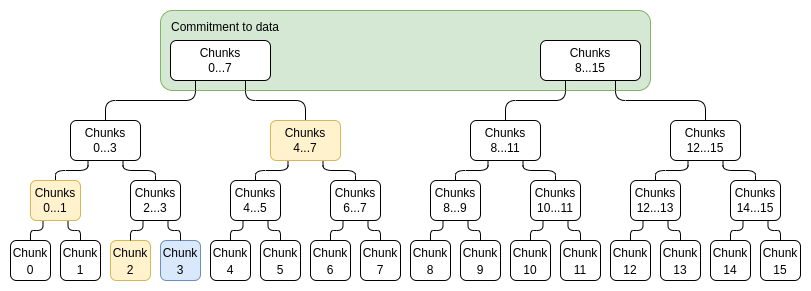
為了證明一個特定的值xi，我們只需提供一個（子承諾，證明）對列表，涵蓋整個範圍0...N−1 或N....2N−1（以包含i 的為準），不包括i，以及一個i不屬於的頂級承諾是正確構建的證明。例如，如果N=8 且i=3，則這個證明將包含C[0,1]、C2、C[4,7] 及其證明，以及一個C[8,15] 被正確構造的證明。該證明將通過驗證各個證明並檢查承諾加起來是否構成完整承諾來進行驗證。

藍色：chunk 3，黃色：chunk 3 的證明。

注意，為了提高效率，每個chunk不需要是一個單獨的評估；相反，我們可以裁剪樹，例如一個chunk是一組16 個評估。鑑於證明的組合大小無論如何都會比這大，像這樣使chunk變大，我們損失很少。

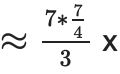
生成這些證明需要O(N∗log(N)) 時間。驗證證明需要O(N) 時間，但請注意，可以批量驗證許多證明：驗證IPA 的O(N) 步驟是橢圓曲線線性組合，我們可以使用隨機線性組合檢查其中的許多。每個證明仍然需要O(N) 場域操作，但這只需要<1 毫秒。

擴展：扇出（fanout）出大於2

我們可以有一個更高的扇出（fanout），而不是每一步都有2扇出，例如8扇出。每個承諾我們將有7 個證明，而不是每個承諾一個證明。例如，在底層，我們將有一個證明{1,2,3,4,5,6,7}，{0,2,3,4,5,6,7}，{0,1 ,3,4 ,5,6,7} 等。這將總證明生成工作增加了

（每個節點7 個證明，每個證明的大小是原始大小的1.75 倍，但層數減少了3 倍，因此~4.08 x 更多的努力），但它將證明大小減少了3 倍。

證明大小

假設我們正在處理大小為32 的N=128 chunk（因此我們有deg<4096 個多項式）和一個(4x, 4x, 8x) 的扇出。單個分支證明將包含3 個IPA，總大小為2∗(7+9+12)=56 個曲線點（~1792 字節）加上chunk的512 字節。今天256 字節或512 字節chunk擁有48 字節證明。

生成證明總共需要2∗8192∗(3∗2+7) 次曲線乘法（兩個fanout-4 層為3 * 2，fanout-8 層為7），或總共~212992 次乘法。因此，這需要一台功能強大的計算機快速完成（普通計算機可以在約50 微秒內完成一次乘法運算，因此這需要10 秒，這有點太長了），或者需要一個分佈式過程，其中不同的節點專注於為不同的chunk。

驗證證明很容易，因為可以批量驗證證明，並且只完成一個橢圓曲線乘法。因此，它不應該比使用KZG 證明慢很多。

自我修復

無法逐列有效地進行自我修復。但是我們能否避免要求單個修復擁有所有數據（來自所有2M 多項式的所有2N chunks）？假設單行完全丟失。很容易使用任何列來重建該列中缺失行中的值。但是如何證明呢？。