lời tựa

lời tựa

Công nghệ bằng chứng không có kiến ​​thức trong mật mã có nhiều ứng dụng trong thế giới web3, bao gồm điện toán cá nhân, zkRollup, v.v. Trong số đó, FOAKS được sử dụng bởi dự án Lớp 2 FOX là một thuật toán chứng minh không có kiến ​​thức. Trong số hàng loạt ứng dụng nêu trên, có hai thuộc tính cực kỳ quan trọng đối với thuật toán zero-knowledge proof, đó là tính hiệu quả và tính tương tác của thuật toán.

Tầm quan trọng của tính hiệu quả của thuật toán là hiển nhiên. Các thuật toán hiệu quả có thể giảm đáng kể thời gian chạy hệ thống, do đó giảm độ trễ của máy khách và cải thiện đáng kể trải nghiệm và hiệu quả của người dùng. Đây cũng là một lý do quan trọng khiến FOAKS cam kết đạt được thời gian kiểm chứng tuyến tính.

Mặt khác, từ góc độ mật mã, việc thiết kế các hệ thống chứng minh không có kiến ​​thức thường dựa trên nhiều vòng tương tác giữa người chứng minh và người xác minh. Ví dụ: trong câu chuyện "Hang động không kiến ​​thức" được sử dụng trong nhiều bài báo khoa học nổi tiếng giới thiệu bằng chứng không kiến ​​thức, việc thực hiện bằng chứng phụ thuộc vào nhiều vòng truyền tải thông tin và tương tác giữa Alibaba (người dẫn chứng) và người báo cáo ( người xác minh). Nhưng trên thực tế, trong nhiều tình huống ứng dụng, việc dựa vào tương tác sẽ khiến hệ thống không còn khả dụng, hoặc làm tăng độ trễ lên rất nhiều. Cũng giống như trong hệ thống zkRollup, chúng tôi hy vọng trình xác minh (nghĩa là thư mục trong FOX) có thể tính toán giá trị bằng chứng chính xác cục bộ mà không phụ thuộc vào tương tác với trình xác minh.

tiêu đề cấp đầu tiên

Thách thức trong Zero Knowledge Proof

Thuật toán chứng minh kiến ​​thức bằng không đã trở nên cực kỳ phổ biến với sự lan rộng của các ứng dụng. Trong những năm gần đây, nhiều thuật toán khác nhau bao gồm FOAKS, Orion và zk-stark cũng đã ra đời. Logic chứng minh cốt lõi của các thuật toán này, cũng như giao thức sigma ban đầu trong lĩnh vực mật mã, là người chứng minh (Prover) trước tiên gửi một giá trị nhất định đến người xác minh (Người xác minh) và người xác minh tạo ra một thách thức (Thách thức) thông qua một số ngẫu nhiên cục bộ. Giá trị thử thách được tạo ngẫu nhiên được gửi đến người chứng minh và người chứng minh cần phải có kiến ​​​​thức thực tế để trả lời với xác suất vượt qua người xác minh cao. Ví dụ, trong hang động không có kiến ​​thức, phóng viên tung đồng xu và bảo Alibaba đi ra từ bên trái hoặc bên phải, "trái và phải" ở đây là thách thức Alibaba, hãy đi ra theo hướng yêu cầu, nếu không thì sẽ có sẽ là một nửa xác suất thất bại.

Ở đây chúng tôi nhận thấy rằng việc tạo ra Thách thức là một bước quan trọng, nó có hai yêu cầu, ngẫu nhiên và không thể đoán trước của tục ngữ. Đầu tiên, tính ngẫu nhiên đảm bảo các thuộc tính xác suất của nó. Điểm thứ hai là nếu người chứng minh có thể dự đoán giá trị thách thức, điều đó có nghĩa là tính bảo mật của giao thức bị phá vỡ. Người chứng minh có thể vượt qua cuộc xác minh mà không cần biết. Phép loại suy có thể được tiếp tục. Nếu Alibaba có thể dự đoán phía nào mà phóng viên hỏi anh ta để đi ra, anh ta sẽ Ngay cả khi không có câu thần chú, bạn có thể vào bên đó trước và kết quả cho thấy rằng bạn có thể vượt qua thỏa thuận.

tiêu đề cấp đầu tiên

Hàm băm

Cái tên hàm băm có lẽ không còn xa lạ với chúng ta, cho dù đó là vấn đề toán học khai thác trong giao thức đồng thuận Bitcoin POW hay nén lượng dữ liệu, xây dựng mã xác minh tin nhắn, v.v., đều có hàm băm. Trong số các giao thức khác nhau được đề cập ở trên, các thuộc tính khác nhau của hàm băm thực sự được sử dụng.

Cụ thể, các thuộc tính của hàm băm an toàn bao gồm:

Khả năng nén: Hàm băm xác định có thể nén một thông báo có độ dài bất kỳ thành một độ dài cố định.

Hiệu quả: Với đầu vào x, dễ dàng tính toán đầu ra h(x).

Chống xung đột: Với một đầu vào x 1 , rất khó để tìm một đầu vào khác x 2 , x 1 x 2 , h(x 1 ) = h(x 2 ).

Lưu ý rằng nếu hàm băm thỏa mãn khả năng chống va chạm, thì nó phải thỏa mãn tính chất một chiều, nghĩa là, với đầu ra y, rất khó để tìm thấy x thỏa mãn h(x) = y. Trong mật mã học, không thể xây dựng một hàm thỏa mãn tuyệt đối tính chất một chiều về mặt lý thuyết, nhưng hàm băm về cơ bản có thể coi là hàm một chiều trong các ứng dụng thực tế.

tiêu đề cấp đầu tiên

Fiat-Shamir Heuristic (Trắc nghiệm)

Trên thực tế, Fiat-Shamir heuristic (Heuristic) là sử dụng hàm băm để băm tập lệnh được tạo trước đó để thu được một giá trị, giá trị này được sử dụng làm giá trị thử thách.

Mô tả hình ảnh

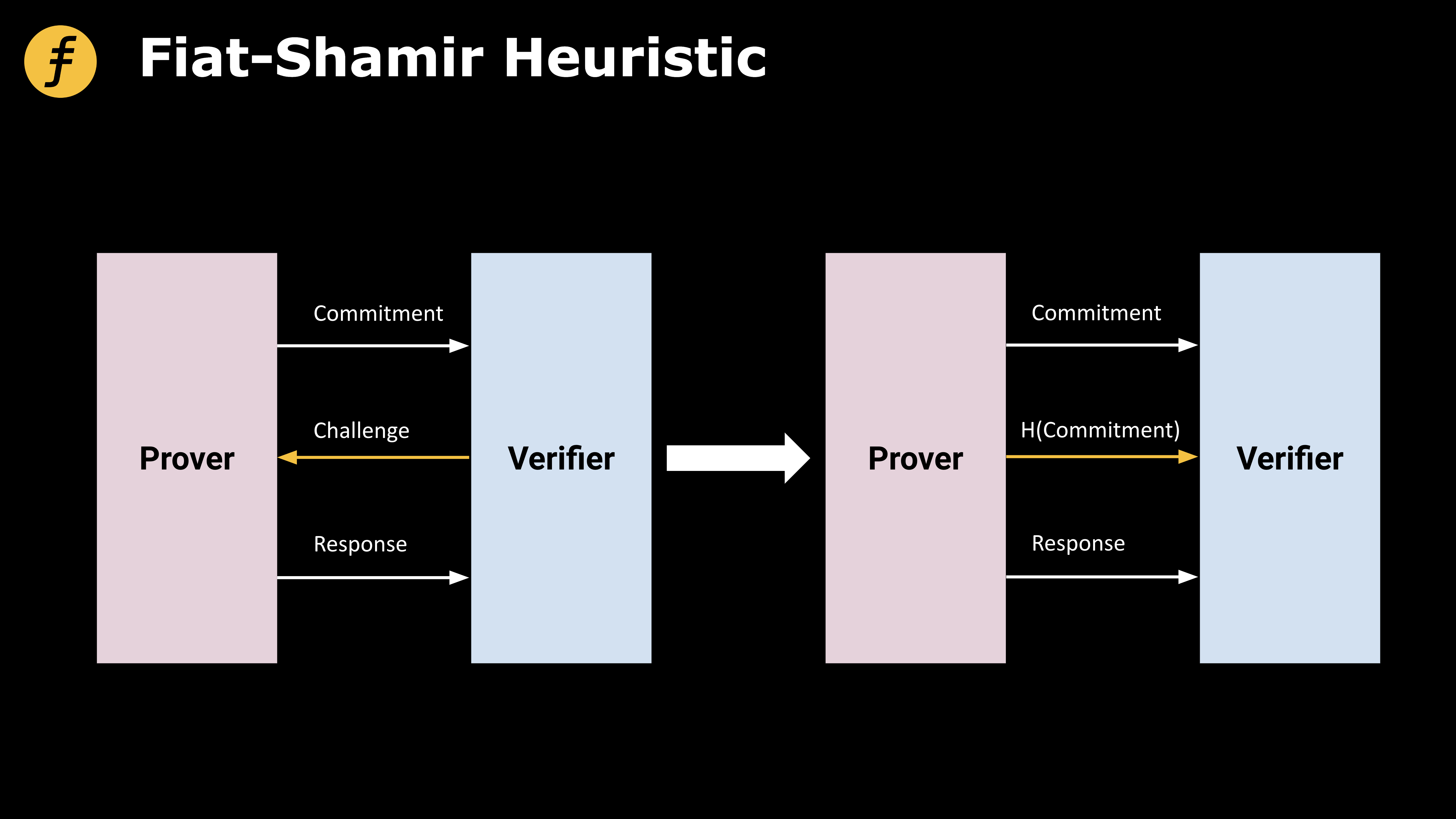
tiêu đề cấp đầu tiên

FOAKS không tương tác

Trong phần này, chúng tôi trình bày cụ thể ứng dụng của kinh nghiệm Fiat-Shamir trong giao thức FOAKS, giao thức này chủ yếu được sử dụng để tạo ra các thử thách trong phần Phanh lại, từ đó nhận ra các FOAKS không tương tác.

Mô tả hình ảnh

Hình 2: Kiểm tra phanh trong FOAKS bằng chứng không tương tác

Bây giờ chúng tôi sử dụng một hàm băm và để người tục ngữ tự tạo ra vectơ ngẫu nhiên này.

Gọi γ0 =H(C1 , R, r0 , r1 ), tương ứng, trong phép tính kiểm định của bộ kiểm định cũng cần bổ sung thêm bước tính γ0 này. Theo cấu trúc này, có thể thấy rằng trước khi tạo ra cam kết, người nói không thể dự đoán trước giá trị thử thách, vì vậy nó không thể "ăn gian" tương ứng theo giá trị thử thách trước, tức là tạo ra giá trị cam kết sai tương ứng. Đồng thời, theo hàm băm Tính ngẫu nhiên của đầu ra hàm, giá trị thử thách cũng thỏa mãn tính ngẫu nhiên.

Đối với điểm thứ hai, đặt Î =H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 ).

phần kết

1. function PC. Commit(ϕ)：

2. Parse was a k × k matrix. The prover locally computes the tensor code encoding C1 ，C2  ，C1  is a k × n matrix，C2  is a n × n matrix.

3. for i ∈ [n] do

4. Compute the Merkle tree root Roott=Merkle.Commit(C2 [:, i])

5. Compute a Merkle tree root R=Merkle.Commit([Root0 ,......Rootn-1 ]), and output R as the commitment.

6. function PC. Prover(ϕ, X, R)

7. The prover generates a random vector γ0  ∈ Fk by computing: γ0 =H(C1 , R, r0 , r1 )

8. Proximity:

   

   
   

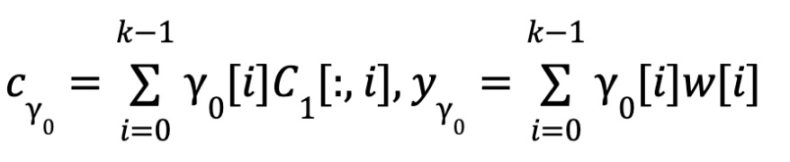
9. Consistency:

   

   
   

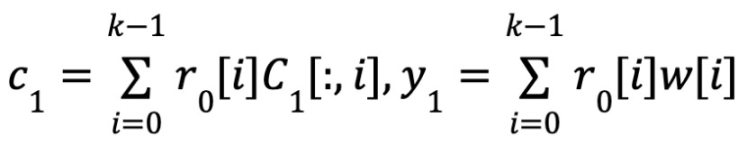
10. Prover sends c1 , y1 , cγ 0 , yγ 0  to the verifier.

11. Prover computes a vector Î as challenge, in which Î = H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 )

12. for idx ∈ Î do

13. Prover sends C1  [:, idx] and the Merkle tree proof of Rootidx for C2  [:, idx] under R to verifier

14. function PC. VERIFY_EVAL(ΠX, X, y= ϕ (X), R)

15. Proximity: ∀idx ∈ Î, Cγ 0 [idx] == <γ0 , C1 [:, idx]> and Ec(yγ 0 ) == Cγ 0 

16. Consistency: ∀idx ∈ Î, C1  [idx] == <γ0 , C1 [:, idx]> and Ec(y1 ) == C1 

17. y==

18. ∀idx ∈ Î, Ec ( C1 [:, idx]) is consistent with ROOTidx, and ROOTidx’s Merkle tree proof is valid.

19. Output accept if all conditions above holds. Otherwise output reject.

phần kết

người giới thiệu

người giới thiệu

1.Fiat, Amos; Shamir, Adi ( 1987). "How To Prove Yourself: Practical Solutions to Identification and Signature Problems". Advances in Cryptology — CRYPTO' 86. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 263: 186 – 194. doi: 10.1007/3-540-47721-7 _ 12. ISBN 978-3-540-18047-0.

2.https://www.cnblogs.com/zhuowangy 2 k/p/12246575.html